山西省大同市2022届高三上学期理数期末考试试卷

试卷更新日期：2022-09-13 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | 2^{x} > 1}$ ， $B = {x | x^{2} + 5 x - 6 < 0}$ ，则 $A ∩ B =$ （）

A、 $(- 1 ， 0)$ B、 $(0 ， 6)$ C、 $(0 ， 1)$ D、 $(- 6 ， 1)$

查看试题解析
2. 设 $z = \frac{1 - i}{1 + i} + 2 i$ ，则 $| z |$ =（）

A、0 B、 $\frac{1}{2}$ C、1 D、 $\sqrt{2}$

查看试题解析
3. 下列命题中，真命题有（）
① $\forall x \in R$ ， $e^{x} - x - 1 \geq 0$ ；② $\exists x_{0} > 0$ ， $l n x_{0} + \frac{1}{l n x_{0}} \leq 2$ ；③若命题 $p \lor q$ 是真命题，则 $\neg p$ 是真命题；④ $y = 2^{x} - 2^{- x}$ 是奇函数．

A、4个 B、3个 C、2个 D、1个

查看试题解析
4. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{2} = 1 (a > \sqrt{2})$ 的两条渐近线的夹角为 $\frac{π}{3}$ ，则a的值为（）

A、 $\frac{\sqrt{6}}{3}$ B、 $\sqrt{6}$ C、 $\frac{\sqrt{6}}{3}$ 或 $\sqrt{6}$ D、 $2 \sqrt{3}$

查看试题解析
5. 下午活动时间，全校进行大扫除，某班卫生委员将包括甲､乙在内的6位同学平均分成3组，分别派到3块班级管辖区域清理卫生，问甲､乙被分到同一个管辖区域的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{5}$ C、 $\frac{1}{4}$ D、 $\frac{1}{3}$

查看试题解析
6. 中国的 $5 G$ 技术领先世界， $5 G$ 技术的数学原理之一便是著名的香农公式： $C = W l o g_{2} (1 + \frac{S}{N})$ .它表示：在受噪音干扰的信道中，最大信息传递速度 $C$ 取决于信道带宽 $W$ ，信道内信号的平均功率 $S$ ，信道内部的高斯噪声功率 $N$ 的大小，其中 $\frac{S}{N}$ 叫做信噪比.当信噪比比较大时，公式中真数里面的1可以忽略不计.按照香农公式，若带宽 $W$ 增大到原来的 $1.2$ 倍，信噪比 $\frac{S}{N}$ 从1000提升到16000，则 $C$ 比原来大约增加了（）
（附： $l g 2 \approx 0.3$ ）

A、32% B、43% C、54% D、68%

查看试题解析
7. 已知数列 ${a_{n}}$ 为等差数列， $S_{n}$ 为其前n项和，若 $a_{4} + a_{7} = 8$ ， $S_{11} = 55$ ，则 $S_{9}$ 等于（）

A、27 B、25 C、20 D、10

查看试题解析
8. 已知(1＋ax)·(1＋x)⁵的展开式中x²的系数为5，则a＝（）

A、－4 B、－3 C、－2 D、－1

查看试题解析
9. 已知 $f (x)$ 是奇函数并且是 $R$ 上的单调函数，若方程 $f (x^{3} + 1) + f (- 3 x - λ) = 0$ 有三个不同的实数解，则实数 $λ$ 的取值范围为（）

A、 $(- 3 ， 1)$ B、 $(- \infty ， - 1) \cup (3 ， + \infty)$ C、 $(- 1 ， 3)$ D、 $(- \infty ， - 3) \cup (1 ， + \infty)$

查看试题解析
10. 若点 $P$ 是圆 $C ： (x + 3)^{2} + (y - 2)^{2} = 1$ 上任一点，则点 $P$ 到直线 $y = k x - 1$ 距离的最大值为（）

A、5 B、6 C、 $3 \sqrt{2} + 1$ D、 $1 + \sqrt{10}$

查看试题解析
11. 如图，已知抛物线 $y^{2} = 4 x$ ，圆 $C ： x^{2} + y^{2} - 2 x = 0$ ，过C点的直线l与抛物线和圆依次交于P，M，N，Q，则 $| P M | \cdot | Q N |$ 等于（）

A、1 B、2 C、4 D、8

查看试题解析
12. 已知三棱锥 $P - A B C$ 的顶点 $P$ 在底面的射影 $O$ 为 $△ A B C$ 的垂心，若 $△ A B C$ 的面积为 $S_{△ A B C} ， △ O B C$ 的面积为 $S_{△ O B C} ， △ P B C$ 的面积为 $S_{△ P B C}$ ，满足 $S_{△ A B C} \cdot S_{△ O B C} = S_{△ P B C}^{2}$ ，当 $△ P A B ， △ P B C ， △ P A C$ 的面积之和的最大值为8时，则三棱锥 $P - A B C$ 外接球的体积为（）

A、 $\frac{4 π}{3}$ B、 $\frac{8 π}{3}$ C、 $\frac{16 π}{3}$ D、 $\frac{32 π}{3}$

查看试题解析

二、填空题

13. 已知 $| \vec{a} | = 1$ ， $\vec{b} = (1 ， \sqrt{3})$ ， $(\vec{b} + \vec{a}) ⊥ \vec{a}$ ，则向量 $\vec{a}$ 与向量 $\vec{b}$ 的夹角为．

查看试题解析
14. 若直线y=2x+a是函数 $f (x) = x + l n x$ 的图象在某点处的切线，则实数a=.

查看试题解析
15. 已知函数 $f (x) = s i n ω x + \sqrt{3} c o s ω x (ω > 0)$ ，且在 $(\frac{π}{3} ， \frac{π}{2})$ 上单调递增，则满足条件的 $ω$ 的最大值为.

查看试题解析
16. 若数列 ${a_{n}}$ 满足 $a_{n + 1} = (- 1)^{n} a_{n} + 2^{n + 1} (n \in N^{*})$ ，令 $S = a_{1} + a_{3} + a_{5} + ⋯ + a_{19} ， T = a_{2} + a_{4} + a_{6} + ⋯ + a_{20}$ ，则 $\frac{T}{S} =$ .

查看试题解析

三、解答题

17. 在 $△ A B C$ 中，角A，B，C的对边分别是a，b，c，且 $2 b c o s C = 2 a + c$ ．

(1)、求角B的大小；

(2)、若 $b = 2 \sqrt{3}$ ， D为AC边上的一点， $B D = 1$ ，且______，求 $△ A B C$ 的面积．
①BD是 $∠ B$ 的平分线；②D为线段AC的中点．（从①，②两个条件中任选一个，补充在上面的横线上并作答）．

查看试题解析
18. 如图所示，点 $P$ 在圆柱的上底面圆周上，四边形 $A B C D$ 为圆柱下底面的内接四边形，且 $A C$ 为圆柱下底面的直径， $P D$ 为圆柱的母线，且 $P D = 3$ ，圆柱的底面半径为1.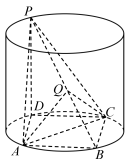

(1)、证明： $A D ⊥ P C$ ；

(2)、 $A D = \sqrt{2} ， B$ 为 $\overset{⌢}{A C}$ 的中点，点 $Q$ 在线段 $P B$ 上，记 $\vec{P Q} = 2 \vec{Q B}$ ，求二面角 $B - A C - Q$ 的余弦值.

查看试题解析
19. 在传染病学中，通常把从致病刺激物侵入机体或者对机体发生作用起，到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.一研究团队统计了某地区1000名患者的相关信息，得到如下表格：
潜伏期（单位：天）
$[0 ， 2]$
$(2 ， 4]$
$(4 ， 6]$
$(6 ， 8]$
$(8 ， 10]$
$(10 ， 12]$
$(12 ， 14]$
人数
50
150
200
300
200
60
40
附： $K^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .
$P (K^{2} ⩾ k_{0})$
0.05
0.025
0.010
$k_{0}$
3.841
5.024
6.635

(1)、求这1000名患者的潜伏期的样本平均数值 $\bar{x}$ （同一组中的数据用该组区间的中点值作代表，结果四舍五入为整数）；

(2)、该传染病的潜伏期受诸多因素的影响，为研究潜伏期与患者年龄的关系，以潜伏期是否超过8天为标准进行分层抽样，从上述1000名患者中抽取200人，得到如下列联表，请将列联表补充完整，并根据列联表判断，能否在犯错误的概率不超过5%的前提下，认为潜伏期与患者年龄有关；

潜伏期 $\leq$ 8天
潜伏期 $> 8$ 天
总计
50岁以上（含50）
100
50岁以下
65
总计
200

(3)、以这1000名患者的潜伏期超过8天的频率，代替该地区1名患者潜伏期超过8天的概率，每名患者的潜伏期是否超过8天相互独立.为了深入研究，该研究团队随机调查了20名患者，其中潜伏期超过8天的人数最有可能（即概率最大）是多少？

查看试题解析
20. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率 $e = \frac{1}{2}$ ，椭圆上的点与左、右顶点所构成三角形面积的最大值为 $2 \sqrt{3}$ ．

(1)、求椭圆 $C$ 的标准方程；

(2)、设过椭圆 $C$ 右焦点的直线 $l_{1}$ ， $l_{2}$ 的斜率分别为 $k_{1}$ ， $k_{2}$ ，满足 $k_{1} \cdot k_{2} = - 2$ ， $l_{1}$ 交 $C$ 于点 $E ， F$ ， $l_{2}$ 交 $C$ 于点 $G ， H$ ，线段 $E F$ 与 $G H$ 的中点分别为 $M ， N$ ．判断直线 $M N$ 是否过定点，若过定点求出该定点；若不过定点，请说明理由．

查看试题解析
21. 已知函数 $f (x) = e^{x} + 2 a x - 1 ， g (x) = 2 a l n (x + 1) - 4 a x ， a \in R$ .

(1)、求函数 $f (x)$ 的单调区间；

(2)、若对任意的 $x \in [0 ， + ∞) ， f (x) + g (x) ⩾ x$ 恒成立，求实数 $a$ 的取值范围.

查看试题解析
22. 在平面直角坐标系xOy中，曲线 $C_{1}$ 的参数方程为 ${\begin{array}{l} x = 2 t^{2} \\ y = 4 t \end{array}$ （t为参数），以坐标原点为极点，x轴正半轴为极轴，建立极坐标系，曲线 $C_{2}$ 的极坐标方程为 $ρ s i n (θ - \frac{π}{4}) = 3 \sqrt{2}$ ．

(1)、写出 $C_{1}$ 的普通方程和 $C_{2}$ 的直角坐标方程；

(2)、设点P在 $C_{1}$ 上，点Q在 $C_{2}$ 上，求 $| P Q |$ 的最小值及此时点P的直角坐标．

查看试题解析
23. 已知函数 $f (x) = | x - 1 | + | x + a |$ ．

(1)、若 $a = 2$ ，求不等式 $f (x) \leq x + 4$ 的解集；

(2)、若 $a > 0$ ， $b > 0$ ， $c > 0$ ，且 $f (x)$ 的最小值为 $4 - b - c$ ，求值： $\frac{1}{a + b} + \frac{1}{c} \geq \frac{4}{3}$ ．

查看试题解析

潜伏期（单位：天）	$[0 ， 2]$	$(2 ， 4]$	$(4 ， 6]$	$(6 ， 8]$	$(8 ， 10]$	$(10 ， 12]$	$(12 ， 14]$
人数	50	150	200	300	200	60	40

	潜伏期 $\leq$ 8天	潜伏期 $> 8$ 天	总计
50岁以上（含50）			100
50岁以下	65
总计			200

$P (K^{2} ⩾ k_{0})$	0.05	0.025	0.010
$k_{0}$	3.841	5.024	6.635