江苏省南通市海安市2021-2022学年高三上学期数学期末考试试卷

试卷更新日期：2022-09-09 类型：期末考试

进入出卷网下载

一、单选题

1. 已知复数z满足(1－i)z＝2＋3i（i为虚数单位），则z＝（）

A、－ $\frac{1}{2}$ ＋ $\frac{5}{2}$ i B、 $\frac{1}{2}$ ＋ $\frac{5}{2}$ i C、 $\frac{1}{2}$ － $\frac{5}{2}$ i D、－ $\frac{1}{2}$ － $\frac{5}{2}$ i

查看试题解析
2. 设集合 $A$ 、 $B$ 均为 $U$ 的子集，如图， $A ∩ (∁_{U} B)$ 表示区域（）

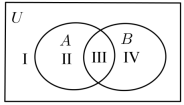A、Ⅰ B、II C、III D、IV

查看试题解析
3. 某校高三年级的700名学生中，男生有385名，女生有315名．从中抽取一个容量为 $60$ 的样本，则抽取男生和女生的人数分别为（）

A、31、29 B、32、28 C、33、27 D、34、26

查看试题解析
4. 通信卫星与经济发展、军事国防等密切关联，它在地球静止轨道上运行，地球静止轨道位于地球赤道所在平面，轨道高度为 $h$ $k m$ （轨道高度是指卫星到地球表面的距离）．将地球看作是一个球（球心为 $O$ ，半径为 $r$ $k m$ ），地球上一点 $A$ 的纬度是指 $O A$ 与赤道平面所成角的度数，点 $A$ 处的水平面是指过点 $A$ 且与 $O A$ 垂直的平面，在点 $A$ 处放置一个仰角为 $θ$ 的地面接收天线（仰角是天线对准卫星时，天线与水平面的夹角），若点 $A$ 的纬度为北纬 $3 0^{∘}$ ，则 $t a n θ =$ （）

A、 $\sqrt{3} - \frac{2 r}{r + h}$ B、 $\sqrt{3} + \frac{2 r}{r + h}$ C、 $\sqrt{3} - \frac{2 h}{r + h}$ D、 $\sqrt{3} + \frac{2 h}{r + h}$

查看试题解析
5. $(1 + \frac{2}{x^{2}}) {(1 + x)}^{6}$ 展开式中 $x^{3}$ 的系数为（）

A、26 B、32 C、46 D、50

查看试题解析
6. 设数列 ${a_{n}}$ 为等比数列，若 $a_{2} + a_{3} + a_{4} = 2$ ， $a_{3} + a_{4} + a_{5} = 4$ ，则数列 ${a_{n}}$ 的前6项和为（）

A、18 B、16 C、9 D、7

查看试题解析
7. 函数 $f (x) = c o s (ω x + \frac{π}{6})$ 的部分图象如图，则下列选项中是其一条对称轴的是（）

A、 $x = \frac{7 π}{24}$ B、 $x = \frac{3 π}{8}$ C、 $x = \frac{5 π}{12}$ D、 $x = \frac{11 π}{24}$

查看试题解析
8. 已知 $a l n 2 = 2 l n a$ ， $b l n 3 = 3 l n b$ ， $c l n 5 = 5 l n c$ ，且 $a ， b ， c \in (0 ， e)$ 则（）

A、c＜a＜b B、a＜c＜b C、b＜a＜c D、b＜c＜a

查看试题解析

二、多选题

9. 下列函数在区间 $(0 ， 1)$ 上单调递增的是（）

A、 $y = {(x - 1)}^{2}$ B、 $y = \frac{1}{1 - x}$ C、 $y = 1 - | x - 1 |$ D、 $y = 2^{- | x |}$

查看试题解析
10. 设 $α$ ， $β$ 为两个平面，下列是“ $α / / β$ ”的充分条件是（）

A、 $α$ ， $β$ 与平面 $γ$ 都垂直 B、 $α$ 内有两条相交直线与平面 $β$ 均无交点 C、异面直线 $a$ ， $b$ 满足 $a / / α$ ， $b / / β$ D、 $α$ 内有5个点（任意三点不共线）到 $β$ 的距离相等

查看试题解析
11. 关于直线 $l ： y = k x + m$ 与圆 $C ： x^{2} + y^{2} = 4$ ，下列说法正确的是（）

A、若 $l$ 与圆 $C$ 相切，则 $m^{2} - 4 k$ 为定值 B、若 $m^{2} - k^{2} = 1$ ，则 $l$ 被圆 $C$ 截得的弦长为定值 C、若 $l$ 与圆 $C$ 有公共点，则 $- 2 \leq m \leq 2$ D、若 $k = m + 1$ ，则 $l$ 与圆 $C$ 相交

查看试题解析
12. 一次抛掷两颗质地均匀的正方体骰子，若出现的点数是2倍关系，则称这次抛掷“漂亮”．规定一次抛掷“漂亮”得分为3，否则得分为－1．若抛掷30次，记累计得分为 $ξ$ ，则（）

A、抛掷一次，“漂亮”的概率为 $\frac{1}{12}$ B、 $ξ$ ＝2时，“漂亮”的次数必为8 C、E( $ξ$ )＝－10 D、 $D (ξ) = \frac{200}{3}$

查看试题解析

三、填空题

13. 在平面直角坐标系xOy中，已知向量 $\vec{a} = (1 ， 2) ， \vec{b} = (- 2 ， - 1)$ ，试写一个非零向量 $\vec{c} =$ ，使得 $\vec{a} \cdot \vec{c} = \vec{b} \cdot \vec{c}$ ．

查看试题解析
14. 若椭圆 $x^{2} + y^{2} c o s θ = 1 (0 < θ < \frac{π}{2})$ 的焦距为 $2$ ，则该椭圆的离心率为．

查看试题解析
15. 已知函数 $f (x) = {\begin{array}{l} x + 1 ， x \leq 0 \\ {(x - 1)}^{2} ， x > 0 \end{array}$ 若 $f (a) = f (b)$ ，则 $| a - b |$ 的最大值为．

查看试题解析
16. 如图，ABCD是一块直角梯形加热片，AB∥CD，∠DAB＝60°，AB＝AD＝4 dm．现将△BCD沿BD折起，成为二面角A－BD－C是90°的加热零件，则AC间的距离是dm；为了安全，把该零件放进一个球形防护罩，则球形防护罩的表面积的最小值是dm² ．（所有器件厚度忽略不计）

查看试题解析

四、解答题

17. 已知数列{an}满足 $2 a_{n} = a_{n + 1} + a_{n + 2}$ ，且 $a_{1} = 1 ， a_{2} = - 1$ ．

(1)、请你在①，②中选择一个证明：
①若 $b_{n} = a_{n} - {a_{n}}_{+ 1}$ ，则{bn}是等比数列；
②若 $b_{n} = 2 a_{n} + {a_{n}}_{+ 1}$ ，则{bn}是等差数列．
注：如果选择多个分别解答，按第一个解答计分．

(2)、求数列{an}的通项公式及其前n项和Sn．

查看试题解析
18. 在平面四边形ABCD中，∠BAD＝2∠ACB＝4∠BAC，AB＝2，BC＝ $\sqrt{6}$ － $\sqrt{2}$ ， CD＝ $\sqrt{13}$ ．

(1)、求∠ACB的大小；

(2)、求四边形ABCD的面积．

查看试题解析
19. 如图，AB是圆O的直径，C是圆O上异于A，B的一点，DC垂直于圆O所在的平面，DC∥EB，DC＝2EB＝2，AB＝4．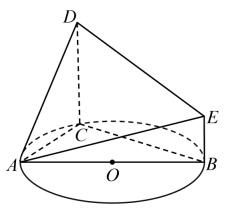

(1)、求证：平面ACD⊥平面EBCD；

(2)、若∠ABC＝30°，求平面ADE与平面ABE所成的锐二面角的余弦值．

查看试题解析
20. 为保护生态环境，减少污染物排放，某厂用“循环吸附降污法”减少污水中有害物，每次吸附后污水中有害物含量y（单位：mg/L）与吸附前的含量x（单位：mg/L）有关，该有害物的排放标准是不超过4 mg/L．现有一批污水，其中该有害物含量为2710 mg/L，5次循环吸附降污过程中的监测数据如下表：

第1次
第2次
第3次
第4次
第5次
吸附前的含量x mg/L
2710
880
290
90
30
吸附后的含量y mg/L
880
290
90
30
10

(1)、已知y关于x的经验回归方程为 $\hat{y} = 0.325 x + \hat{a}$ ．请你预测首次达到排放标准时有害物的含量；

(2)、视（1）中所求的预测含量为实际排放含量，排放前，取n份处理后的污水样品检测该有害物的含量．已知检测结果的误差zn~N（0， $\frac{1}{n}$ ）（zn单位：mg），至少要取多少份样品检测，才能确保检测结果符合排放标准的概率不小于0.9987．
附：若X~N（μ，σ²），则P（|X－μ|≤3σ）≈0.9974）．

查看试题解析
21. 已知双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ $(a > 0 ， b > 0)$ 的两条渐近线互相垂直，且过点 $D (\sqrt{2} ， 1)$ ．

(1)、求双曲线 $C$ 的方程；

(2)、设 $P$ 为双曲线的左顶点，直线 $l$ 过坐标原点且斜率不为 $0$ ， $l$ 与双曲线 $C$ 交于 $A$ ， $B$ 两点，直线 $m$ 过 $x$ 轴上一点 $Q$ （异于点 $P$ ），且与直线 $l$ 的倾斜角互补， $m$ 与直线 $P A$ ， $P B$ 分别交于 $M ， N$ （ $M ， N$ 不在坐标轴上）两点，若直线 $O M$ ， $O N$ 的斜率之积为定值，求点 $Q$ 的坐标．

查看试题解析
22. 已知函数 $f (x) = e^{x} - a \sqrt{x}$ (a∈R)．

(1)、若 $f (x)$ 是单调增函数，求a的取值范围；

(2)、若 $x_{1}$ ， $x_{2}$ 是函数 $f (x)$ 的两个不同的零点，求证： $1 < x_{1} + x_{2} < 2 l n a - l n 2$ ．

查看试题解析

	第1次	第2次	第3次	第4次	第5次
吸附前的含量x mg/L	2710	880	290	90	30
吸附后的含量y mg/L	880	290	90	30	10