湖北省新高考联考协作体2021-2022学年高三上学期数学期末联考试卷

试卷更新日期：2022-09-09 类型：期末考试

进入出卷网下载

一、单选题

1. 设集合 $A = {- 1 ， 0 ， 1 ， 2}$ ， $B = {x | 2^{x} < 2}$ ，则 $A ∩ B =$ （）

A、 $(- 1 ， 0 ， 1)$ B、 $(- 1 ， 0)$ C、 ${- 1 ， 0}$ D、 ${- 1 ， 0 ， 1}$

查看试题解析
2. 已知 $\vec{a}$ ， $\vec{b}$ 为单位向量，且 $| 2 \vec{a} - \vec{b} | = \sqrt{3}$ ，则 $\vec{a}$ ， $\vec{b}$ 的夹角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
3. 设 $a = 3^{0.2}$ ， $b = l o g_{0.2} 3$ ， $c = s i n (- 202 1^{∘})$ ，则（）

A、 $c < b < a$ B、 $b < c < a$ C、 $a < b < c$ D、 $b < a < c$

查看试题解析
4. 已知复数数列 ${a_{n}}$ 满足 $a_{1} = 2 i$ ， $a_{n + 1} = i a_{n} + i + 1$ ， $n \in N^{*}$ ，（ $i$ 为虚数单位），则 $a_{10} =$ （）

A、 $2 i$ B、 $- 2 i$ C、 $1 + i$ D、 $- 1 + i$

查看试题解析
5. 若函数 $y = f (x)$ 的大致图象如图所示，则 $f (x)$ 的解析式可能是（）

A、 $f (x) = \frac{x}{| x | - 1}$ B、 $f (x) = \frac{x}{1 - | x |}$ C、 $f (x) = \frac{x}{x^{2} - 1}$ D、 $f (x) = \frac{x}{1 - x^{2}}$

查看试题解析
6. 在2021中俄高加索联合军演的某一项演练中，中方参加演习的有4艘军舰，5架飞机；俄方有3艘军舰，6架飞机.若从中、俄两方中各选出2个单位（1架飞机或一艘军舰都作为一个单位，所有的军舰两两不同，所有的飞机两两不同），且选出的四个单位中恰有一架飞机的不同选法共有（）

A、51种 B、168种 C、224种 D、336种

查看试题解析
7. 已知 $F_{1}$ 、 $F_{2}$ 分别是双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左右焦点，点 $P$ 在双曲线右支上且不与顶点重合，过 $F_{2}$ 作 $∠ F_{1} P F_{2}$ 的角平分线的垂线，垂足为 $A$ ， $O$ 为坐标原点，若 $| O A | = b$ ，则该双曲线的离心率为（）

A、 $\sqrt{2}$ B、 $\frac{2 \sqrt{3}}{3}$ C、2 D、 $\frac{\sqrt{5}}{2}$

查看试题解析
8. 足球起源于中国东周时期的齐国，当时把足球称为“蹴鞠”.汉代蹴鞠是训练士兵的手段，制定了较为完备的体制.如专门设置了球场，规定为东西方向的长方形，两端各设六个对称的“鞠域”，也称“鞠室”，各由一人把守.比赛分为两队，互有攻守，以踢进对方鞠室的次数决定胜负.1970年以前的世界杯用球多数由举办国自己设计，所以每一次球的外观都不同，拼块的数目如同掷骰子一样没准.自1970年起，世界杯官方用球选择了三十二面体形状的足球，沿用至今.如图Ⅰ，三十二面体足球的面由边长相等的12块正五边形和20块正六边形拼接而成，形成一个近似的球体.现用边长为 $4.5 c m$ 的上述正五边形和正六边形所围成的三十二面体的外接球作为足球，其大圆圆周展开图可近似看成是由4个正六边形与4个正五边形以及2条正六边形的边所构成的图形的对称轴截图形所得的线段 $A A^{'}$ ，如图Ⅱ，则该足球的体积约为（）
参考数据： $t a n 72 ° \approx 3.1$ ， $\sqrt{3} \approx 1.7$ ， $π \approx 3$ ， $22 . 5^{2} = 506.25$ ， $22 . 5^{3} = 11390.62$ .

A、 $5695.31 c m^{3}$ B、 $2847.66 c m^{3}$ C、 $1518.75 c m^{3}$ D、 $1488.85 c m^{3}$

查看试题解析

二、多选题

9. 若两函数的定义域、单调区间、奇偶性、值域都相同，则称这两函数为“伙伴函数”.下列函数中与函数 $f (x) = x^{4}$ 不是“伙伴函数”是（）

A、 $y = 2^{| x |} - 1$ B、 $y = \frac{x^{2}}{1 + x^{2}}$ C、 $y = \frac{x^{2}}{2} + c o s x - 1$ D、 $y = l n | x |$

查看试题解析
10. 下列说法不正确的是（）

A、若 $\vec{a} = (1 ， 2)$ ， $\vec{b} = (1 ， - 1)$ ，且 $\vec{a}$ 与 $\vec{a} + λ \vec{b}$ 的夹角为锐角，则 $λ$ 的取值范围是 $(- \infty ， 5)$ B、若A，B， $C$ 不共线，且 $\vec{O P} = 2 \vec{O A} - 4 \vec{O B} + 3 \vec{O C}$ ，则P，A，B、C四点共面 C、对同一平面内给定的三个向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ ，一定存在唯一的一对实数 $λ$ ， $μ$ ，使得 $\vec{a} = λ \vec{b} + μ \vec{c}$ . D、 $△ A B C$ 中，若 $\vec{A B} \cdot \vec{B C} < 0$ ，则 $△ A B C$ 一定是钝角三角形.

查看试题解析
11. 如图，点 $N$ 为边长为1的正方形 $A B C D$ 的中心， $△ E C D$ 为正三角形，平面 $E C D ⊥$ 平面 $A B C D$ ， $M$ 是线段 $E D$ 的中点，则（）

A、直线 $B M$ 、 $E N$ 是异面直线 B、 $B M \neq E N$ C、直线 $B M$ 与平面 $E C D$ 所成角的正弦值为 $\frac{\sqrt{21}}{7}$ D、三棱锥 $N - E C D$ 的体积为 $\frac{\sqrt{3}}{24}$

查看试题解析
12. 设函数 $f (x) = x l n x$ ， $g (x) = \frac{f^{'} (x)}{x}$ ，则下列说法正确的有（）

A、不等式 $g (x) > 0$ 的解集为 $(\frac{1}{e} ， + \infty)$ ； B、函数 $g (x)$ 在 $(0 ， e)$ 单调递增，在 $(e ， + ∞)$ 单调递减； C、当 $x \in (\frac{1}{e} ， 1)$ 时，总有 $f (x) < g (x)$ 恒成立； D、若函数 $F (x) = f (x) - a x^{2}$ 有两个极值点，则实数 $a \in (0 ， \frac{1}{2})$

查看试题解析

三、填空题

13. 设 $(5 x - \sqrt{x})^{n}$ 的展开式的各项系数之和为M，二项式系数之和为N，若 $M - N = 240$ ，则展开式中 $x^{3}$ 的系数为．

查看试题解析
14. 在等差数列 ${a_{n}}$ 中， $a_{1} + a_{7} = 14$ ，当 $a_{3}^{2} + a_{4}^{2} + a_{5}^{2}$ 取得最小值时， $a_{2022} =$ .

查看试题解析
15. 设 $x > 0$ ， $y > 0$ ，且 ${(x - \frac{1}{y})}^{2} = \frac{16 y}{x}$ ，则当 $x + \frac{1}{y}$ 取最小值时， $x^{2} + \frac{1}{y^{2}} =$ .

查看试题解析
16. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - 4 y^{2} = 1 (a > 0)$ 的右顶点到其一条渐近线的距离等于 $\frac{\sqrt{3}}{4}$ ，抛物线 $E ： y^{2} = 2 p x$ 的焦点与双曲线 $C$ 的右焦点重合，则抛物线 $E$ 上的动点 $M$ 到直线 $l_{1} ： 4 x - 3 y + 6 = 0$ 和 $l_{2} ： x = - 1$ 的距离之和的最小值为．

查看试题解析

四、解答题

17. 在 $△ A B C$ 中，角 $A ， B ， C$ 的对边分别是 $a ， b ， c$ ， $△ A B C$ 的面积为 $S$ .

(1)、若 $a = 2$ ， $b = 3$ ， $S = \frac{3}{2} \sqrt{3}$ ，求边 $c$ ；

(2)、若 $△ A B C$ 是锐角三角形且角 $A = 2 B$ ，求 $\frac{a}{b}$ 的取值范围.

查看试题解析
18. 设等比数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且 $a_{n + 1} = 2 S_{n} + 1$ ， $(n \in N^{*})$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、在 $a_{n}$ 与 $a_{n + 1}$ 之间插入 $n$ 个实数，使这 $n + 2$ 个数依次组成公差为 $d_{n}$ 的等差数列，设数列 ${\frac{1}{d_{n}}}$ 的前 $n$ 项和为 $T_{n}$ ，求证： $T_{n} < \frac{15}{8}$ .

查看试题解析
19. 如图，在多面体 $A B C D F E$ 中，四边形 $A B C D$ 是边长为2的正方形，四边形 $A B E F$ 是直角梯形，其中 $∠ A B E = 90 °$ ， $A F / / B E$ ，且 $D E = A F = 3 B E = 3$ .

(1)、证明：平面 $A B E F ⊥$ 平面 $A B C D$ .

(2)、求二面角 $C - D E - F$ 的余弦值.

查看试题解析
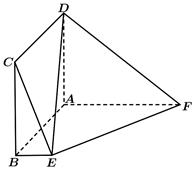20. 某种项目的射击比赛，开始时选手在距离目标 $100 m$ 处射击，若命中则记3分，且停止射击．若第一次射击未命中，可以进行第二次射击，但需在距离目标 $150 m$ 处，这时命中目标记2分，且停止射击．若第二次仍未命中，还可以进行第三次射击，此时需在距离目标 $200 m$ 处，若第三次命中则记1分，并停止射击．若三次都未命中则记0分，并停止射击．已知选手甲的命中率与目标的距离的平方成反比，他在 $100 m$ 处击中目标的概率为 $\frac{1}{2}$ ，且各次射击都相互独立．

(1)、求选手甲在射击中得0分的概率；

(2)、设选手甲在比赛中的得分为 $ξ$ ，求 $ξ$ 的分布列和数学期望．

查看试题解析
21. 已知点 $F_{1}$ 、 $F_{2}$ 分别是椭圆C的左、右焦点，离心率为 $\frac{\sqrt{2}}{2}$ ，点P是以坐标原点O为圆心的单位圆上的一点，且 $\vec{P F_{1}} \cdot \vec{P F_{2}} = 0$ ．

(1)、求椭圆C的标准方程；

(2)、设斜率为k的直线l（不过焦点）交椭圆于M，N两点，若x轴上任意一点到直线 $M F_{1}$ 与 $N F_{1}$ 的距离均相等，求证：直线l恒过定点，并求出该定点的坐标．

查看试题解析
22. 已知函数 $f (x) = - \frac{a}{x} + l n x$

(1)、讨论函数 $f (x)$ 的单调性；

(2)、若 $a = 1$ ，证明： $f (\frac{1}{x}) > - e^{x}$

查看试题解析