黑龙江省八校2021-2022学年高三上学期理数期末联合考试试卷

试卷更新日期：2022-09-09 类型：期末考试

进入出卷网下载

一、单选题

1. 抛物线 $y = \frac{1}{16} x^{2}$ 的准线方程是（）

A、 $x = \frac{1}{16}$ B、 $y = - \frac{1}{16}$ C、 $x = - 4$ D、 $y = - 4$

查看试题解析
2. 某几何体的三视图如图所示，则其体积为（）

A、4 B、 $\frac{7}{3}$ C、 $\frac{4}{3}$ D、 $\frac{8}{3}$

查看试题解析
3. 若 $t a n α = 2$ ，则 $c o s (\frac{3 π}{2} - 2 α) + c o s 2 α =$ （）

A、 $- \frac{7}{5}$ B、 $- \frac{1}{5}$ C、 $\frac{1}{5}$ D、 $\frac{7}{5}$

查看试题解析
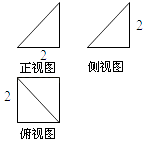4. “ $m = 5$ ”是“直线 $3 x + 4 y - m = 0$ 与圆 $(x - 1)^{2} + (y + 2)^{2} = 4$ 相切”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 已知函数 $f (x)$ 为 $R$ 上偶函数，且 $f (x)$ 在 $[0 ， + \infty)$ 上的单调递增，若 $f (2) = - 2$ ，则满足 $f (x - 1) \geq - 2$ 的 $x$ 的取值范围是（）

A、 $(- \infty ， - 1) \cup (3 ， + \infty)$ B、 $(- \infty ， - 1] \cup [3 ， + \infty)$ C、 $[- 1 ， 3]$ D、 $(- \infty ， - 2] \cup [2 ， + \infty)$

查看试题解析
6. 已知 $m$ ， $n$ 为两条不同直线， $α$ ， $β$ 为两个不同平面，给出下列命题：
① ${\begin{array}{l} m ⊥ α \\ m ⊥ n \end{array} \Rightarrow n / / α$ ；② ${\begin{array}{l} m ⊥ β \\ n ⊥ β \end{array} \Rightarrow m / / n$ ；③ ${\begin{array}{l} m ⊥ α \\ m ⊥ β \end{array} \Rightarrow α / / β$ ；④ ${\begin{array}{l} m \subset α \\ n \subset β \\ α / / β \end{array} \Rightarrow m / / n$ .
其中正确命题的序号是：（）

A、②③ B、③④ C、①② D、①④

查看试题解析
7. 直线 $l$ 过点 $(1 ， 2)$ ，且纵截距为横截距的两倍，则直线 $l$ 的方程是（）

A、 $2 x - y = 0$ B、 $2 x + y - 4 = 0$ C、 $2 x - y = 0$ 或 $2 x + y - 4 = 0$ D、 $2 x - y = 0$ 或 $2 x + y - 2 = 0$

查看试题解析
8. 已知 $a > 0$ ， $b > 0$ ，两直线 $l_{1} ： (a - 1) x + y - 1 = 0$ ， $l_{2} ： x + 2 b y + 1 = 0$ ，且 $l_{1} ⊥ l_{2}$ ，则 $\frac{1}{a} + \frac{2}{b}$ 的最小值为（）

A、2 B、4 C、8 D、9

查看试题解析
9. 在矩形 $A B C D$ 中， $A B = \sqrt{3} A D = 3 ， \vec{D C} = 4 \vec{M C} ， \vec{B P} = λ \vec{B C}$ ，且 $\vec{A D} \cdot \vec{A P} = 2$ ，则 $\vec{A M} \cdot \vec{D P} =$ （）

A、 $\frac{23}{4}$ B、5 C、 $\frac{19}{4}$ D、4

查看试题解析
10. 如图，过抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点 $F$ 的直线 $l$ 交抛物线于点A、B，交其准线于点C，若 $| B C | = 2 | B F |$ ，且 $| A F | = 6$ ，则 $p$ 的值为（）

A、2 B、3 C、4 D、5

查看试题解析
11. 已知函数 $f (x) = {\begin{array}{l} | x + 1 | ， x \leq 0 ， \\ l n x + 1 ， x > 0 ， \end{array}$ 若方程 $f (x) = m (m \in R)$ 恰有三个不同的实数解a，b，c（ $a < b < c$ ），则 $(a + b) c$ 的取值范围是（）.

A、 $[- 2 ， - \frac{2}{e})$ B、 $(e - 1 ， 2)$ C、 $(- 2 ， 2 e)$ D、 $[- e ， 2]$

查看试题解析
12. 设 $a = \frac{4 (2 - \ln 4)}{e^{2}}$ ， $b = \frac{1}{e}$ ， $c = \frac{\ln 4}{4}$ ，则 $a$ ， $b$ ， $c$ 的大小顺序为（）

A、 $a < c < b$ B、 $c < a < b$ C、 $a < b < c$ D、 $b < a < c$

查看试题解析

二、填空题

13. 若实数 $x$ ， $y$ 满足约束条件 ${\begin{array}{l} x - y + 2 \geq 0 \\ x - 2 y \leq 0 \\ x + 2 y - 4 \leq 0 \end{array}$ ，则 $x + y$ 的最小值为

查看试题解析
14. 直线 $y = x + 1$ 与圆 $(x - 3)^{2} + (y - 2)^{2} = 4$ 交于A，B原点，O为坐标原点，则弦 $| A B |$ 的长度为.

查看试题解析
15. 若双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的离心率为 $\sqrt{5}$ ，则其渐近线方程为.

查看试题解析
16. 已知AB是椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ 一条弦，且弦AB与直线 $l ： x + 2 y - 3 = 0$ 垂直，P是AB的中点，O为椭圆的中心，则直线OP斜率是.

查看试题解析

三、解答题

17. 在△ $A B C$ 中，内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，且 ${(s i n A - s i n C)}^{2} = s i n^{2} B - s i n A s i n C$ ．

(1)、求 $s i n B$ ；

(2)、若 $a = 2 c$ ，且△ $A B C$ 的面积为 $2 \sqrt{3}$ ，求△ $A B C$ 的周长．

查看试题解析
18. 已知数列 ${a_{n}}$ 中，其前 $n$ 项和 $S_{n}$ 满足 $S_{n} = 2^{n + 1} - 2$ $(n \in N_{+})$ .

(1)、求证：数列 ${a_{n}}$ 为等比数列，并求 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = (n + 1) \cdot a_{n}$ ，求数列 ${b_{n}}$ 的前项和 $T_{n}$ .

查看试题解析
19. 已知圆 $C ： x^{2} + y^{2} + 2 x - 6 y + 6 = 0$ ．

(1)、若圆 $C^{^{'}} ： x^{2} + y^{2} = 4$ 与圆 $C$ 关于直线 $l$ 对称，求直线 $l$ 的方程；

(2)、若过点 $P (1 ， 0)$ 的直线 $l$ 与圆 $C$ 相切，求直线 $l$ 的方程；

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中，PD⊥平面ABCD，四边形ABCD是矩形，点E是PC的中点， $P D = C D = 2 B C = 2$ .

(1)、求异面直线PA与DE所成角的余弦值；

(2)、证明：PA $∥$ 平面BDE；

(3)、求二面角 $E - B D - C$ 的余弦值.

查看试题解析
21. 已知函数 $f (x) = (x - 1) e^{x}$

(1)、求 $f (x)$ 的最值；

(2)、若 $f (x) + e^{x} \geq l n x + x + a$ 对 $x \in (0 ， + \infty)$ 恒成立，求 $a$ 的取值范围.

查看试题解析
22. 已知双曲线 $E ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 过点 $D (3 ， 1)$ ，且该双曲线的虚轴端点与两顶点 $A_{1} ， A_{2}$ 的张角为 $120 °$ ．

(1)、求双曲线 $E$ 的方程；

(2)、过点 $B (0 ， 4)$ 的直线 $l$ 与双曲线 $E$ 左支相交于点 $M ， N$ ，直线 $D M ， D N$ 与 $y$ 轴相交于 $P ， Q$ 两点，求 $| B P | + | B Q |$ 的取值范围．

查看试题解析