江苏省泰州市兴化市2022-2023学年九年级上学期开学数学试卷

试卷更新日期：2022-09-09 类型：开学考试

进入出卷网下载

一、选择题（每题3分，共18分）

1. 如图是四款新能源汽车的标志，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列式子中，属于分式的是（）

A、 $\sqrt{x} -$ 1 B、x²+1 C、 $\frac{π}{2}$ D、 $\frac{1}{x}$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{{(- 3)}^{2}} =$ ±3 B、 $\sqrt{3^{2}} =$ ±3 C、 $\sqrt{{(- 3)}^{2}} = -$ 3 D、 $- \sqrt{3^{2}} = -$ 3

查看试题解析
4. 用配方法解方程x²+2x﹣1＝0时，配方结果正确的是（）

A、（x+2）²＝2 B、（x+1）²＝2 C、（x+2）²＝3 D、（x+1）²＝3

查看试题解析
5. 已知反比例函数y $= - \frac{8}{x}$ ，下列说法不正确的是（）

A、图像经过点（2，﹣4） B、图像分别在二、四象限 C、当y≤1时，x≤﹣8 D、在每个象限内，y随x增大而增大

查看试题解析
6. 在平行四边形ABCD中，AB＝3，BC＝4，当平行四边形ABCD的面积最大时，①BD＝5；②∠A+∠C＝180°；③AC⊥BD；④AC＝BD．以上4个结论中正确的有（）

A、①②③ B、①②④ C、②③④ D、①③④

查看试题解析

二、填空题（每题3分，共27分）

7. 如果 $\frac{2 x}{x - 1}$ 有意义，则x的取值范围为．

查看试题解析
8. 化简： $\frac{x}{x - 2} - \frac{2}{x - 2}$ ＝.

查看试题解析
9. 已知m，n是方程x²+2x﹣5＝0的两个实数根，则mn+m+n＝．

查看试题解析
10. 反比例函数y $= \frac{k}{x}$ （x＞0）的图像如图所示，则k的取值范围是．

查看试题解析
11. 如图，在⊙O中，半径r＝10，弦AB＝16，P是弦AB上的动点，则线段OP长的最小值为．

查看试题解析
12. 如图，在Rt△ABC中，∠ACB＝90°，D，E，F分别是边AB，AC，BC的中点．若CD的长为3，则EF的长是．

查看试题解析
13. 若一元二次方程ax²＝b（ab＞0）的两个不相等的根分别是2m+1与m﹣7，则 $\frac{a}{b}$ 为．

查看试题解析
14. 关于x的方程 $\frac{3 x - m}{x + 3} =$ 4的解是负数，则m的取值范围是．

查看试题解析
15. 如图，点M是反比例函数y $= \frac{8}{x}$ （x＞0）图像上一点，将点M绕原点O逆时针旋转45°后，恰好落在y轴的正半轴上，则线段OM的长为．

查看试题解析

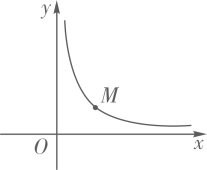
三、解答题（共8题，共75分）

16.

(1)、计算：（ $\sqrt{3}$ ）²﹣（ $π - \sqrt{5}$ ）⁰ $- \sqrt{27} -$ | $\sqrt{3} -$ 2|；

(2)、化简： $\frac{b}{a^{2} - b^{2}} \div$ （1 $- \frac{a}{a + b}$ ）．

查看试题解析
17. 解方程：

(1)、2x²﹣3x﹣1＝0；

(2)、 $\frac{6}{x - 2} = \frac{x}{x + 3} - 1$ ．

查看试题解析
18. 已知关于x的一元二次方程x²+（k+2）x+2k＝0．

(1)、求证：方程总有两个实数根；

(2)、若该方程有一个根是正数，求k的取值范围．

查看试题解析
19. 为保障新冠病毒疫苗接种需求，某生物科技公司开启“加速”模式，生产效率比原先提高了20%，现在生产480万剂疫苗所用的时间比原先生产420万剂疫苗所用的时间少1天．问原先每天生产多少万剂疫苗？

查看试题解析
20. 已知：如图，菱形ABCD，分别延长AB，CB到点F，E，使得BF＝BA，BE＝BC，连接AE，EF，FC，CA．

(1)、求证：四边形AEFC为矩形；

(2)、连接DE交AB于点O，如果DE⊥AB，AB＝4，求DE的长．

查看试题解析
21. 如图，已知AB是⊙O的直径，⊙O交△ABE边AE于点D，连接OD，且满足OD∥BE，点P在BA的延长线上，PD交BE于点C．

(1)、求证：AB＝BE；

(2)、如果PA＝2，∠B＝60°，PC⊥BE，求直径AB的长．

查看试题解析
22. 已知：正方形ABCD中，M为BC上一点．

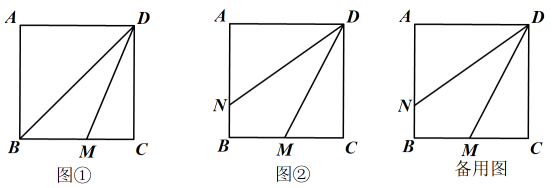(1)、如图①，若DM为∠BDC的平分线，CM $= \sqrt{2}$ ，求CD的长；

(2)、如图②所示，若M为BC中点，N为AB上的点，且DM为∠NDC的平分线．
①求证：DN＝BN+AD；

②点P为边BC上任一点，将线段DP绕点D顺时针旋转90°，得到线段DQ，连接PQ，无论点P在BC边上如何运动，PQ≥2 $\sqrt{2}$ 总成立，求BN的长．

查看试题解析
23. 已知点A（3，m+2），B（m+4，2）都在反比例函数y $= \frac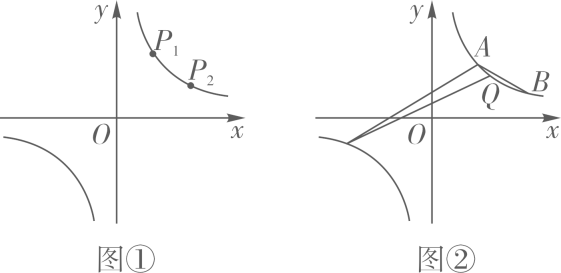{k}{x}$ 的图像上．

(1)、求m，k的值；

(2)、如图①，已知反比例函数y $= \frac{k}{x}$ 的图像上有两点P₁（x₁ ， y₁），P₂（x₂ ， y₂），且0＜x₁＜x₂＜3，分别过P₁ ， P₂向x轴作垂线，垂足分别为M₁ ， M₂ ，过P₁ ， P₂向y轴作垂线，垂足分别为N₁ ， N₂ ．若记四边形P₁M₁ON₁和四边形P₂M₂ON₂的周长分别为C₁ ， C₂ ，试比较C₁和C₂的大小；并说明理由．

(3)、如图②，若点B关于原点O对称点为C，点Q为双曲线AB段上任一动点，试探究∠ACQ与∠ABQ大小关系，并说明理由．

查看试题解析