浙江省杭州市萧山区六校联考2022-2023学年九年级上学期期初数学试卷

试卷更新日期：2022-09-09 类型：开学考试

进入出卷网下载

一、选择题（本大题共10小题，共30分。）

1. 如图是厨余垃圾、可回收物、有害垃圾和其他垃圾的标识，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 2021年春节，为了预防新冠肺炎疫情，各地纷纷响应“原地过年”的倡导，假期七天，全国铁路，公路，水路，民航共发送旅客大约98400000人次，比去年同期下降 $34.8 %$ .数据98400000用科学记数法表示为（）

A、 $984 \times 10^{5}$ B、 $98.4 \times 10^{6}$ C、 $9.84 \times 10^{8}$ D、 $9.84 \times 10^{7}$

查看试题解析
3. 下列计算结果正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 $\frac{\sqrt{6}}{\sqrt{3}} = 2$ D、 ${(- \sqrt{5})}^{2} = 5$

查看试题解析
4. 测试五位学生的“一分钟仰卧起坐”成绩，得到五个各不相同的数据. 在统计时，出现了一处错误：将最高成绩50个写成了55个.则下列统计量不受影响的是（）

A、方差 B、标准差 C、中位数 D、平均数

查看试题解析
5. 下列各选项中因式分解正确的是（）

A、 $x^{2} - 1 = {(x - 1)}^{2}$ B、 $a^{3} - 2 a^{2} + a = a^{2} (a - 2)$ C、 $- 2 y^{2} + 4 y = - 2 y (y + 2)$ D、 $m^{2} n - 2 m n + n = n {(m - 1)}^{2}$

查看试题解析
6. 在平面直角坐标系中， $P$ 点关于原点的对称点为 $P_{1} (- 3 ， - \frac{8}{3})$ ， $P$ 点关于 $x$ 轴的对称点为 $P_{2} (a ， b)$ ，则 $\sqrt[3]{a b} =$ （）

A、-2 B、2 C、4 D、-4

查看试题解析
7. 要确定方程 $x^{2} + x - 5 = 0$ 的解，只需知道一次函数 $y = x + 1$ 和反比例函数 $y = \frac{k}{x}$ 的图象交点的横坐标．由上面的信息可知， $k$ 的值为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤，然后剪出图⑤中的阴影部分，则阴影部分展开铺平后的图形是（）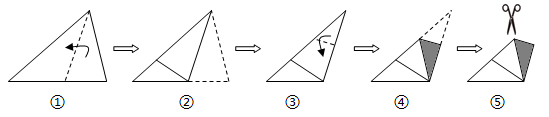

A、等腰三角形 B、直角三角形 C、矩形 D、菱形

查看试题解析
9. 某旅行社组织游客到楠溪江乘坐竹筏漂流，若租用8座的竹筏 $x$ 排，则余下6人无座位；若租用12座的竹筏则可少租用1排，且最后一排竹筏还没坐满，则乘坐最后一排12座竹筏的人数是 $($ $)$

A、 $(18 - 4 x)$ 人 B、 $(6 - 4 x)$ 人 C、 $(30 - 4 x)$ 人 D、 $(18 - 8 x)$ 人

查看试题解析
10. 如图，在菱形纸片 $A B C D$ 中， $∠ A = 60 °$ ，将菱形纸片翻折，使点 $A$ 落在 $C D$ 的中点 $P$ 处，折痕为 $M N$ ，点 $M$ ， $N$ 分别在边 $A B$ ， $A D$ 上，则 $B M$ ： $A M$ 的值为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{7}$ C、 $\frac{1}{6}$ D、 $\frac{1}{5}$

查看试题解析

二、填空题（本大题共6小题，共24分）

11. 一个多边形的每个外角都等于72°，则这个多边形的边数为．

查看试题解析
12. 已知一组数据：2，3，4，5，6，则这组数据的标准差是 .

查看试题解析
13. 由不等式 $a x > b$ 可以推出 $x < \frac{b}{a}$ ，那么 $a$ 的取值范围是．

查看试题解析
14. 已知分式 $\frac{5 x + n}{x + m}$ （m、n为常数）满足表格中的信息：

$x$ 的取值

-2

0.4

$q$

分式的值

无意义

0

3

则 $q$ 的值是．

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $A B = 2$ ， $A D = 1$ ，点 $E$ 为边 $C D$ 上的一点 $($ 与 $C$ 、 $D$ 不重合 $)$ ，四边形 $A B C E$ 关于直线 $A E$ 的对称图形为四边形 $A N M E$ ，延长 $M E$ 交 $A B$ 于点 $P$ ，当 $D E = \frac{3}{4}$ 时， $△ P A E$ 的面积为．

查看试题解析
16. 已知函数 $y_{1} = \frac{k}{x} (k$ 为常数，且 $k > 0$ ， $x > 0)$ ，函数 $y_{2}$ 的图象和函数 $y_{1}$ 的图象关于直线 $y = 1$ 对称．
$①$ 若函数 $y_{2}$ 的图象上的点的纵坐标为 $b$ ，则 $b$ 的取值范围为．

$②$ 若当 $m \leq x \leq 2$ （m为大于 $0$ 的实数）时， $y_{1}$ 的最大值为 $a$ ，则在此取值范围内， $y_{2}$ 的最小值为．

查看试题解析

三、解答题（本大题共7小题，共66分。）

17. 以下是方方化简 $(2 x + y) (2 x - y) + 4 (x + y)^{2}$ 的解答过程．
解： $(2 x + y) (2 x - y) + 4 (x + y)^{2}$
$= 4 x^{2} - y^{2} + 4 (x^{2} + y^{2})$
$= 4 x^{2} - y^{2} + 4 x^{2} + y^{2}$
$= 8 x^{2}$ ．
方方的解答过程是否有错误？如果有错误，写出正确的解答过程．

查看试题解析
18. 计算：

(1)、计算： $\sqrt{12} - (\sqrt{\frac{1}{3}} - \sqrt{1 \frac{1}{3}})$ ；

(2)、解方程： $x^{2} - 6 x = 7$ .

查看试题解析
19. 为讴歌抗击新冠肺炎的白衣战士，某校七年级举行了“新时代最可爱的人”主题演讲比赛 $.$ 七年级甲，乙两班分别选5名同学参加比赛 $.$ 如图是根据其预赛成绩绘制的折线统计图，请你根据统计图提供的信息完成以下问题：

(1)、求甲班成绩的中位数和乙班成绩的众数；

(2)、学校决定在甲，乙两班中选取预赛成绩较好的5人参加该活动的区级比赛，求这5人预赛成绩的平均数．

查看试题解析
20. 如图，在△ABC中，D，E分别是AB，AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．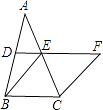

(1)、求证：四边形BCFE是菱形；

(2)、若CE=4，∠BCF=120°，求菱形BCFE的面积．

查看试题解析
21. 已知：关于 $x$ 的一元二次方程 $k x^{2} - (4 k - 3) x + 3 k - 3 = 0$

(1)、求证：无论 $k$ 取何值，方程都有实根；

(2)、若 $x = - 1$ 是该方程的一个根，求 $k$ 的值；

(3)、若方程的两个实根均为正整数，求 $k$ 的值 $(k$ 为整数 $)$ ．

查看试题解析
22. 已知反比例函数 $y_{1} = \frac{k}{x}$ 的图象经过 $(3 ， 2)$ ， $(m ， n)$ 两点.

(1)、求 $y_{1}$ 的函数表达式；

(2)、当 $m < 1$ 时，求 $n$ 的取值范围；

(3)、设一次函数 $y_{2} = a x - 3 a + 2 (a > 0)$ ，当 $x > 0$ 时，比较 $y_{1}$ 与 $y_{2}$ 的大小.

查看试题解析
23. 已知正方形 $A B C D$ ，点 $F$ 是射线 $D C$ 上一动点 $($ 不与 $C$ 、 $D$ 重合 $)$ ，连接 $A F$ 并延长交直线 $B C$ 于点 $E$ ，交 $B D$ 于点 $H$ ，连接 $C H$ ，过点 $C$ 作 $C G ⊥ H C$ 交 $A E$ 于点 $G$ ．

(1)、若点 $F$ 在边 $C D$ 上，如图 $1$ ．
$①$ 证明： $∠ D A H = ∠ D C H$ ；

$②$ 猜想线段 $C G$ 与 $E F$ 的关系并说明理由；

(2)、取 $D F$ 中点 $M$ ，连结 $M G$ ，若 $M G = 4$ ，正方形边长为6，求 $B E$ 的长．

查看试题解析

$x$ 的取值	-2	0.4	$q$
分式的值	无意义	0	3