陕西省西安市2022-2023学年九年级上学期开学数学试卷
试卷更新日期:2022-09-09 类型:开学考试
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 下列方程是一元二次方程的是A、 B、 C、 D、2. 矩形具有而菱形不具有的性质是( )A、对边相等 B、对角线互相垂直 C、邻边垂直 D、对角线互相平分3. 随着生产技术的进步,某制药厂生产成本逐年下降,两年前生产一吨药的成本是6000元,现在生产一吨药的成本是5000元.设生产成本的年平均下降为 , 下列所列的方程正确的是A、 B、 C、 D、4. 在不透明的袋子中装有黑、白两种球共50个,这些球除颜色外都相同,随机从袋中摸出一个球,记录下颜色后,放回袋子中并摇匀,再从中摸出一个球,经过如此大量重复试验,发现摸出的黑球的频率稳定在0.4附近,则袋子中黑球的个数约为A、20个 B、30个 C、40个 D、50个5. 用配方法解一元二次方程 , 下面配方正确的是A、 B、 C、 D、6. 某班级计划举办手抄报展览,确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题,若小明和小亮每人随机选择其中一个主题,则他们恰好选择同一个主题的概率是( )A、 B、 C、 D、7. 已知m是一元二次方程的一个根,则的值是( )A、4 B、6 C、8 D、108. 关于的一元二次方程有A、两个相等的实数根 B、两个不相等的正数根 C、两个不相等的负数根 D、一个正数根和一个负数根9. 如图,四边形和四边形是两个矩形,点在边上,若 , , 则矩形的面积为
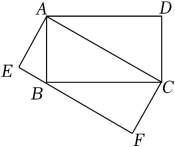 A、2 B、 C、 D、10. 已知关于的一元二次方程有实数根,设此方程的一个实数根为 , 令 , 则( )A、 B、 C、 D、
A、2 B、 C、 D、10. 已知关于的一元二次方程有实数根,设此方程的一个实数根为 , 令 , 则( )A、 B、 C、 D、二、填空题(本大题共5小题,每题4分,共20分)
-
11. 若是关于的一元二次方程,则的值为 .12. 已知一元二次方程有一根为1,则的值为 .13. “双减”政策后,各校积极探索“课内提质增效,课后丰富多彩”的有效策略,某校的课后服务活动设置了四大板块课程: . 体育活动;劳动技能;经典阅读;科普活动.若小明和小亮两人随机选择一个板块课程,则两人所选的板块课程恰好相同的概率是 .14. 如图,是正方形的对角线上一点,连接 , 过点作 , 垂足为点 . 若 , , 则正方形的面积为 .
 15. 如图,已知在中, , , , 在边上方作等边 , 则的长为 .
15. 如图,已知在中, , , , 在边上方作等边 , 则的长为 .
三、解答题(本大题共5小题,共50分)
-
16. 解方程:(1)、(用配方法解);(2)、;(3)、;(4)、 .17. 一次圆桌会议设有4个座位,主持人坐在了如图所示的座位上,嘉宾甲、乙、丁3人等可能地坐到①、②、③中的3个座位上,请用所学的概率知识求嘉宾甲与乙相邻而坐的概率.
 18. 金都百货某小家电经销商销售一种每个成本为40元的台灯,当每个台灯的售价定为60元时,每周可卖出100个,经市场调查发现,该台灯的售价每降低2元.其每周的销量可增加20个.(1)、台灯单价每降低4元,平均每周的销售量为 个.(2)、如果该经销商每周要获得利润2240元,那么这种台灯的售价应降价多少元?(3)、在(2)的条件下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
18. 金都百货某小家电经销商销售一种每个成本为40元的台灯,当每个台灯的售价定为60元时,每周可卖出100个,经市场调查发现,该台灯的售价每降低2元.其每周的销量可增加20个.(1)、台灯单价每降低4元,平均每周的销售量为 个.(2)、如果该经销商每周要获得利润2240元,那么这种台灯的售价应降价多少元?(3)、在(2)的条件下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?