北京市通州区2022届高三上学期数学期末考试试卷

试卷更新日期：2022-09-08 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {- 1 ， 0 ， 1 ， 2}$ ， $B = {x | 0 < x < 4}$ ，则 $A ∩ B =$ （）

A、 ${- 1 ， 0 ， 1 ， 2 ， 3}$ B、 ${- 1 ， 0 ， 1}$ C、 ${0 ， 1}$ D、 ${1 ， 2}$

查看试题解析
2. 复数 $z = i \cdot (1 + i)$ 在复平面上对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 双曲线 $\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1$ 的渐近线方程是（）

A、 $y = \pm \frac{3}{4} x$ B、 $y = \pm \frac{3}{5} x$ C、 $y = \pm \frac{4}{3} x$ D、 $y = \pm \frac{5}{3} x$

查看试题解析
4. 已知数列 ${a_{n}}$ 是公比为正数的等比数列， $S_{n}$ 是其前 $n$ 项和， $a_{2} = 2$ ， $a_{4} = 8$ ，则 $S_{7} =$ （）

A、31 B、63 C、127 D、255

查看试题解析
5. “直线 $l$ 与直线 $m$ 没有公共点”是“ $l ∥ m$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
6. 若 $a < b < 0$ ，则下列不等式成立的是（）

A、 $a^{2} < b^{2}$ B、 ${(\frac{1}{2})}^{a} < {(\frac{1}{2})}^{b}$ C、 $l o g_{3} | a | < l o g_{3} | b |$ D、 $\frac{b}{a} + \frac{a}{b} > 2$

查看试题解析
7. 函数 $f (x) = c o s 2 x + s i n^{2} x$ 是（）

A、奇函数，且最大值为2 B、奇函数，且最大值为1 C、偶函数，且最大值为2 D、偶函数，且最大值为1

查看试题解析
8. 北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”一亮相，好评不断，这是一次中国文化与奥林匹克精神的完美结合．为了宣传2022年北京冬奥会和冬残奥会，某学校决定派小明和小李等5名志愿者将两个吉祥物安装在学校的体育广场，每人参与且只参与一个吉祥物的安装，每个吉祥物都至少由两名志愿者安装．若小明和小李必须安装不同的吉祥物，则不同的分配方案种数为（）

A、8 B、10 C、12 D、14

查看试题解析
9. 经过点 $(2 ， 1)$ 的直线与圆 $O ： x^{2} + y^{2} = 25$ 交于 $A$ ， $B$ 两点，则 $△ O A B$ 面积的最大值为（）

A、 $2 \sqrt{6}$ B、 $2 \sqrt{21}$ C、10 D、 $\frac{25}{2}$

查看试题解析
10. 中国茶文化博大精深．茶水的口感与茶叶类型和水的温度有关．经验表明，有一种茶用85℃的水泡制，再等到茶水温度降至55℃时饮用，可以产生最佳口感．某研究人员在室温下，每隔1min测一次茶水温度，得到数据如下：
放置时间/min
0
1
2
3
4
5
茶水温度/℃
85.00
79.00
73.60
68.74
64.37
60.43
为了描述茶水温度 $y ℃$ 与放置时间 $x m i n$ 的关系，现有以下两种函数模型供选择：
① $y = k a^{x} + 25 (k \in R ， 0 < a < 1 ， x \geq 0)$ ， ② $y = k x + b (k ， b \in R ， x \geq 0)$ ．
选择最符合实际的函数模型，可求得刚泡好的茶水达到最佳口感所需放置时间大约为（）
（参考数据： $l g 2 \approx 0.301$ ， $l g 3 \approx 0.477$ ）

A、6min B、6.5min C、7min D、7.5min

查看试题解析

二、填空题

11. 抛物线 $y^{2} = 4 x$ 的焦点坐标是．

查看试题解析
12. 最小正周期为2的函数的解析式可以是．（写出一个即可）

查看试题解析
13. 如图，圆锥 $P O$ 的体积为 $V_{1}$ ，过 $P O$ 的中点 $O^{'}$ 作平行于底面的截面，以该截面为底面挖去一个圆柱，设圆柱体积为 $V_{2}$ ，则 $V_{1} ： V_{2} =$ ．

查看试题解析
14. 已知函数 $f (x) = e^{x} - | x + a |$ ，给出下列四个结论：
①若 $a = 0$ ，则 $f (x)$ 有一个零点；②若 $a \in [1 ， + \infty)$ ，则 $f (x)$ 有三个零点；③ $\forall a \leq 0$ ， $f (x)$ 在R上是增函数；④ $\exists a > 0$ ，使得 $f (x)$ 在R上是增函数．
其中所有正确结论的序号是．

查看试题解析
15. 已知平面向量 $\vec{a}$ ， $\vec{b}$ 的夹角为120°，且 $| \vec{a} | = 2$ ， $| \vec{b} | = 4$ ，则 $\vec{a} \cdot \vec{b}$ 的值为， $| \vec{a} - t \vec{b} | (t \in R)$ 的最小值为．

查看试题解析

三、解答题

16. 在 $△ A B C$ 中， $s i n A = \sqrt{2} s i n B$ ， $b = \sqrt{2}$ ．再从条件①，条件②、条件③这三个条件中选择一个作为已知，使 $△ A B C$ 存在且唯一确定，并解决下面的问题：

(1)、求角 $B$ 的大小；

(2)、求 $△ A B C$ 的面积．
条件①： $c = 4$ ；条件②： $b^{2} - a^{2} = c^{2} - \sqrt{2} a c$ ；条件③： $a c o s B = b s i n A$ ．

查看试题解析
17. 如图，在长方体 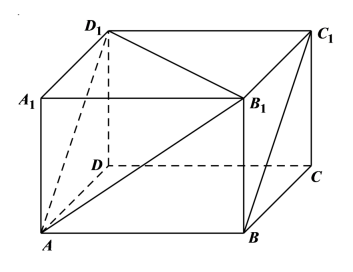$A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 2$ ， $B C = C C_{1} = 1$ ．

(1)、求证： $B C_{1} / /$ 平面 $A B_{1} D_{1}$ ；

(2)、求平面 $A B_{1} D_{1}$ 与平面 $A B C D$ 夹角的余弦值；

(3)、求点 $B$ 到平面 $A B_{1} D_{1}$ 的距离．

查看试题解析
18. 人类常见的遗传病类型主要分为单基因遗传病、多基因遗传病和染色体异常遗传病三大类，高度近视（600度以上）、红绿色盲都是较常见的单基因遗传病．某学校课后实践活动对学生这两种遗传病情况进行统计，分别从男、女同学中各随机抽取100人进行调查，对患病情况统计如下，其中“√”表示是，“×”表示否．
人数
男生
高度近视
红绿色盲
3
√
×
√
2
√
√
×
1
√
√
√
1
×
×
√
2
×
√
×

(1)、分别估计该校男生红绿色盲的发病率和该校女生红绿色盲的发病率；

(2)、为做家庭访问，从已调查出患红绿色盲的同学中任选两人，记这两人中男同学人数为 $X$ ，求 $X$ 的分布列及数学期望；

(3)、假设该校男生人数为1500，女生人数为2500，试估计该校学生高度近视发病率 $M$ 与该校学生红绿色盲发病率 $N$ 的大小关系，并说明理由．
（注： $某种遗传病发病率 = \frac{某种遗传病的患者数}{某种遗传病的被调查人数} \times 100 %$ ）

查看试题解析
19. 已知函数 $f (x) = \frac{2 a x + 4 a^{2} - 1}{x^{2} + 4} (a \neq 0)$ ．

(1)、若 $a = \frac{1}{2}$ ，求曲线 $y = f (x)$ 在点 $(0 ， f (0))$ 处的切线方程；

(2)、求 $f (x)$ 的单调区间与极值．

查看试题解析
20. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点 $(0 ， 1)$ ，离心率为 $\frac{\sqrt{2}}{2}$ ．

(1)、求椭圆 $C$ 的方程；

(2)、直线 $y = k (x + 1) (k \neq 0)$ 与椭圆交于 $A$ 、 $B$ 两点，过 $A$ 、 $B$ 作直线 $l ： x = - 2$ 的垂线，垂足分别为 $M$ 、 $N$ ，点 $G$ 为线段 $M N$ 的中点， $F$ 为椭圆 $C$ 的左焦点．求证：四边形 $A G N F$ 为梯形．

查看试题解析
21. 已知数列 ${a_{n}}$ 满足以下条件：① $a_{n} \in N *$ ，且 $1 \leq a_{n} \leq 100$ ；②共有100项，且各项互不相等．定义数列 $A_{i} ： a_{i} ， a_{i + 1} ， a_{i + 2} ， ⋯ ， a_{i + 9} (i = 1 ， 2 ， 3 ， ⋯ ， 91)$ 为数列 ${a_{n}}$ 的一个“10阶连续子列”．

(1)、若 ${a_{n}}$ 的通项公式为 $a_{n} = n$ ，写出 ${a_{n}}$ 的一个“10阶连续子列”，并求其各项和；

(2)、求证：对于每个 ${a_{n}}$ ，都至少有一个10阶连续子列的各项和不小于505；

(3)、若对于每个 ${a_{n}}$ ，都至少有一个10阶连续子列的各项和不小于正整数 $M$ ，求 $M$ 的最大值．

查看试题解析

放置时间/min	0	1	2	3	4	5
茶水温度/℃	85.00	79.00	73.60	68.74	64.37	60.43

人数	男生	高度近视	红绿色盲
3	√	×	√
2	√	√	×
1	√	√	√
1	×	×	√
2	×	√	×