2022年苏科版初中数学七年级上册 3.3 代数式的值（2）同步练习

试卷更新日期：2022-09-08 类型：同步测试

进入出卷网下载

一、单选题

1. 如图是一个简单的数值运算程序，若输入x的值为3，则输出的数值为（）

A、5 B、7 C、8 D、10

查看试题解析
2. 如图所示是计算机某计算程序，若开始输入x=3，则最后输出的结果是（）.

A、10 B、12 C、38 D、42

查看试题解析
3. 按下图程序计算，若开始输入的值为x=3，则最后输出的结果是（）

A、6 B、21 C、156 D、231

查看试题解析
4. 按如图所示的程序计算，若开始输入的数为 $x = 5$ ，则最后输出的结果是（）

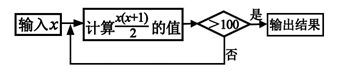A、15 B、30 C、105 D、120

查看试题解析
5. 按下面的程序计算：

若输入n=100，输出结果是501；若输入n=25，输出结果是631，若开始输入的n值为正整数，最后输出的结果为781，则开始输入的n值可能有（）

A、1种 B、2种 C、4种 D、5种

查看试题解析
6. 如图是一个简单的数值运算程序，当输入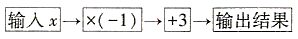 $x = - 1$ 时，输出的数值为.

查看试题解析
7. 如图所示是一个数值运算程序，若输入x＝﹣5，则输出的结果y是.

查看试题解析
8. 如图是一个数值转换机，如果输出的结果为﹣9，那么输入的数x是．

查看试题解析
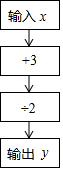9. 如图所示是计算机某计算程序，若开始输入 $x = - 2$ ，则最后输出的结果是

查看试题解析
10. 如图所示的运算程序中，若输入的 $x$ 值为－2，则输出的 $y$ 的值为 .

查看试题解析
11. 已知a的绝对值等于2，b的倒数为-1，c与-3互为相反数，求a+b+c的值

查看试题解析
12. 张师傅承揽了某栋公寓楼的装修任务，他准备铺地时，发现这栋公寓楼户型结构相同，但地面卫生间和客厅的宽分别有几个类型，他将房子地面结构图按下图进行表示（单位：米）．

(1)、请你用含 $x$ ， $y$ 的式子，帮张师傅把地面的总面积表示出来；（单位：平方米）

(2)、已知 $x = 4.5$ ， $y = 2$ 这类型的房子有五户，铺地砖的费用为80元/平方米，请求出这个类型的房子铺地砖的总费用．

查看试题解析
13.

(1)、已知 $| a | = 5$ ， $| b | = 3$ ，且 $| a - b | = b - a$ ，求 $a + b$ 的值；

(2)、已知a与b互为相反数，c与d互为倒数，x的绝对值等于5，求 $x^{2} + (a + b) x - {(c d)}^{2021}$ 的值.

查看试题解析

二、填空题

14. 如图，这是一个数值转换机的示意图，若输入x的值为﹣5，则输出的结果为（）

A、﹣10 B、﹣15 C、﹣30 D、﹣40

查看试题解析
15. 如图是一个运算程序：

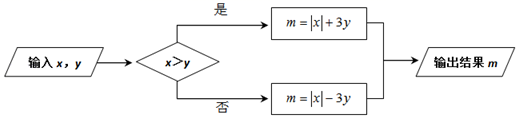
若x＝﹣1，输出结果m的值与输入y的值相同，则y的值为（　　）

A、 $- \frac{1}{4}$ B、 $- \frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
16. 按如图的运算程序，能使输出的结果为12的是（）.

A、 $x = - 4$ ， $y = 2$ B、 $x = - 4$ ， $y = - 2$ C、 $x = - 2$ ， $y = 4$ D、 $x = - 3$ ， $y = - 4$

查看试题解析
17. 观察如图所示的程序，若输出的结果为3，则输入的x值为（）

A、1 B、﹣2 C、﹣1或2 D、1或2

查看试题解析
18. 按如图所示的运算程序，若输出结果为y＝﹣3，则输入x的值可以是（）

A、﹣3 B、﹣1 C、1 D、3

查看试题解析
19. 按如图所示的运算程序，能使输出结果为1的是（　　）

A、x＝0，y＝1 B、x＝﹣1，y＝0 C、x＝1，y＝0 D、x＝1，y＝1

查看试题解析
20. 如图是一个数值转换机，例如输入a＝5，第一步5²＝25，第二步25﹣4×5＝5，第三步5×（﹣3），输出结果为﹣15．若输入a＝﹣6，则输出结果应为．

查看试题解析
21. 按照如图所示的计算程序，若输入x＝2，则输出的结果为．

查看试题解析
22. 小星在学习“设计自己的运算程序”综合与实践课后，设计了如图所示的运算程序．若开始输入的x值为2，则最后输出的结果y是．

查看试题解析
23. 在如图的计算程序中，若输入x的值为1，则输出结果为．

查看试题解析
24. 按照如图所示的操作步骤，若输入的值为-4，则输出的值为.

查看试题解析
25. 如图所示的运算程序中，若开始输入的x值为36，我们发现第1次输出的结果为18，第2次输出的结果为9，…第2020次输出的结果为.

查看试题解析
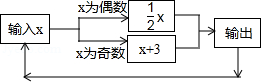26. 把（a-2b）看作一个“字母”，化简多项式-3a（a-2b）⁵+6b（a-2b）⁵-5（-a+2b）³ ，并求当a-2b=-1时的值．

查看试题解析
27. 已知a、b互为相反数，c、d互为倒数，m的绝对值是5，n是最大的负整数，求代数式2011（a+b）-4cd+2mn的值．

查看试题解析
28. 已知 ${(x + 1)}^{6} = a x^{6} + b x^{5} + c x^{4} + d x^{3} + e x^{2} + f x + g$ .
当 $x = 1$ 时， ${(1 + 1)}^{6} = a \times 1^{6} + b \times 1^{5} + c \times 1^{4} + d \times 1^{3} + e \times 1^{2} + f \times 1 + g$

$∴ a + b + c + d + e + f + g = 2^{6} = 64$

这种给x取一个特殊数的方法叫赋值法.请你巧用赋值法，尝试解答下列问题.

(1)、当x为多少时，可求出g为多少？

(2)、求 $a - b + c - d + e - f + g$ 的值；

(3)、求 $a + c + e$ 的值.

查看试题解析

三、延伸拓展

29. 数轴上点A表示﹣10，点B表示10，点C表示18，如图，将数轴在原点O和点B处各折一下，得到一条“折线数轴”，在“折线数轴”上，点M、N表示的数分别是m、n，我们把m、n之差的绝对值叫做点M，N之间友好距离，即MN＝|m﹣n|.例如点A和点C在折线数轴上友好距离28个长度单位.动点P从点A出发，以2单位/秒的速度沿着折线数轴的正方向运动，从点O运动到点B期间速度变为原来的一半；点P从点A出发的同时，点Q从点C出发，以1单位/秒的速度沿着“折线数轴”的负方向运动（假定运动过程中Q速度一直保持不变），当点P到达B点时，点P、Q均停止运动.设运动的时间为t秒.问：

(1)、当t＝4秒时，P、Q友好距离个单位长度，当t＝14秒时P、Q友好距离个单位长度.

(2)、当P、Q两点友好距离是2个单位长度时，t＝秒.

(3)、P、Q两点相遇时，求运动的时间t的值.

查看试题解析
30. 在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的“探究”.
（提出问题）三个有理数a、b、c满足abc>0，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值.

（解决问题）由题意得：a ， b，c三个有理数都为正数或其中一个为正数，另两个为负数.

①当a ， b，c都是正数，即a>0，b>0，c>0时，

则： $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ = $\frac{a}{a} + \frac{b}{b} + \frac{c}{c}$ =1+1+1=3；

②当a ， b，c有一个为正数，另两个为负数时，设a>0，b<0，c<0，

即： $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ = $\frac{a}{a} + \frac{- b}{b} + \frac{- c}{c}$ =1+（−1）+（−1）=−1，所以 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值为3或−1.

(1)、（探究）请根据上面的解题思路解答下面的问题：
已知a<0，b>0，c>0，则 $\frac{| a |}{a} =$ ， $\frac{| b |}{b} =$ ， $\frac{| c |}{c} =$ ；

(2)、三个有理数a ， b，c满足abc<0，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值；

(3)、已知|a|=3，|b|=1，且a<b，求a+b的值.

查看试题解析

2022年苏科版初中数学七年级上册 3.3 代数式的值（2） 同步练习

一、单选题

二、填空题

三、延伸拓展

2022年苏科版初中数学七年级上册 3.3 代数式的值（2）同步练习