山西省朔州市怀仁市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-08 类型:期末考试
一、单选题
-
1. 若 , 则a的值为( )A、4 B、-4 C、-2 D、2. 下面调查方式中,合适的是( )A、试航前对我国第一艘国产航母各系统的检查,选择抽样调查方式 B、了解一批袋装食品是否含有防腐剂,选择普查方式 C、为有效控制“新冠疫情”的传播,对国外入境人员的健康状况,采用普查方式 D、调查某新型防火材料的防火性能,采用普查的方式3. 如图,坐标平面上有原点O与A、B、C、D四点.若有一直线l通过点(-3,4)且与y轴垂直,则l也会通过下列哪一点?( )
 A、A B、B C、C D、D4. 下列图形中,已知∠1=∠2,则可得到 AB∥CD 的是( )A、
A、A B、B C、C D、D4. 下列图形中,已知∠1=∠2,则可得到 AB∥CD 的是( )A、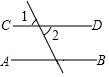 B、
B、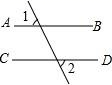 C、
C、 D、
D、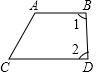 5. 判断命题“如果 ,那么 ”是假命题,只需举出一个反例,反例中的n可以为( )A、-2 B、 C、0 D、6. 下列说法错误的是( )A、由 , 得 B、由得 C、不等式的解一定是不等式的解 D、若 , 则(c为有理数)7. 已知二元一次方程组 , 如果用加减法消去n,则下列方法可行的是( )A、①×4+②×5 B、①×5+②×4 C、①×5﹣②×4 D、①×4﹣②×58. 一道来自课本的习题:
5. 判断命题“如果 ,那么 ”是假命题,只需举出一个反例,反例中的n可以为( )A、-2 B、 C、0 D、6. 下列说法错误的是( )A、由 , 得 B、由得 C、不等式的解一定是不等式的解 D、若 , 则(c为有理数)7. 已知二元一次方程组 , 如果用加减法消去n,则下列方法可行的是( )A、①×4+②×5 B、①×5+②×4 C、①×5﹣②×4 D、①×4﹣②×58. 一道来自课本的习题:从甲地到乙地先有一段上坡路后有一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54分钟,从乙地到甲地需42分钟,甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,采用间接设法:
设坡路有x km,平路有y km,则全程为(x+y)km.已经列出一个方程 , 则另一个方程正确的是( )
A、 B、 C、 D、9. 为节约用电,某市根据每户居民每月用电量分为三档频数户收费.第一档电价:每月用电量低于240度,每度0.48元;第二档电价:每月用电量为度,每度0.53元;第三档电价:每月用电量超过400度,每度0.78元小明同学对该市有1000居民的某小区月用电量(单位:度)进行了抽样调查,绘制了如图所示的统计图.下列说法不合理的是 A、本次抽样调查的样本容量为50 B、估计该小区按第一档电价交费的居民户数最多 C、该小区按第二档电价交费的居民有240户 D、该小区按第三档电价交费的居民比例约为10. 已知方程组 的解满足 ,则m取值范围是( )A、m>1 B、m<-1 C、m>-1 D、m<1
A、本次抽样调查的样本容量为50 B、估计该小区按第一档电价交费的居民户数最多 C、该小区按第二档电价交费的居民有240户 D、该小区按第三档电价交费的居民比例约为10. 已知方程组 的解满足 ,则m取值范围是( )A、m>1 B、m<-1 C、m>-1 D、m<1二、填空题
-
11. 在实数0, , , 中,最小的数是 .12. 如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于 .
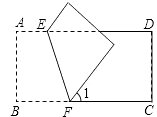 13. 在一次体育测试中,10名女生完成仰卧起坐的个数如下:38、52、47、46、50、53、61、72、45、58,则10名女生仰卧起坐个数不少于50个的频率为.14. 已知是关于x,y的二元一次方程,则mn= .15. 在“新冠肺炎”这场没有硝烟的战争中,各行各业都涌现出了一批“最美逆行者”,其中抗疫最前沿的就是护士。某医院护安排护士若干名负责护理新冠病人,每名护士护理4名新冠病人,有20名新冠病人没人护理,如果每名护士护理8名新冠病人,有一名护士护理的新冠病人多于1人不足8人,这个医院安排了名护士护理新冠病人。
13. 在一次体育测试中,10名女生完成仰卧起坐的个数如下:38、52、47、46、50、53、61、72、45、58,则10名女生仰卧起坐个数不少于50个的频率为.14. 已知是关于x,y的二元一次方程,则mn= .15. 在“新冠肺炎”这场没有硝烟的战争中,各行各业都涌现出了一批“最美逆行者”,其中抗疫最前沿的就是护士。某医院护安排护士若干名负责护理新冠病人,每名护士护理4名新冠病人,有20名新冠病人没人护理,如果每名护士护理8名新冠病人,有一名护士护理的新冠病人多于1人不足8人,这个医院安排了名护士护理新冠病人。三、解答题
-
16.(1)、计算:;(2)、解方程:17. 解方程组:(1)、;(2)、18. 解不等式(组):(1)、 , 把解集在数轴上表示出来;(2)、 , 求出它的所有整数解的和.19. 如图,已知点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠FBD, . 求证:∠E=∠F.
 20. 如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,的三个顶点均在格点上.
20. 如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,的三个顶点均在格点上. (1)、将先向右平移6个单位长度,再向上平移3个单位长度,得到 , 画出平移后的;(2)、建立适当的平面直角坐标系,使得点的坐为;(3)、在(2)的条件下,直接写出点的坐标.21. 为庆祝建校60周年,某校组织七年级学生进行“方阵表演”.为了整齐划一,需了解学生的身高,现随机抽取该校七年级学生进行抽样调查,根据所得数据绘制出如下计图表:
(1)、将先向右平移6个单位长度,再向上平移3个单位长度,得到 , 画出平移后的;(2)、建立适当的平面直角坐标系,使得点的坐为;(3)、在(2)的条件下,直接写出点的坐标.21. 为庆祝建校60周年,某校组织七年级学生进行“方阵表演”.为了整齐划一,需了解学生的身高,现随机抽取该校七年级学生进行抽样调查,根据所得数据绘制出如下计图表:组别
身高


根据图表提供的信息,回答下列问题:
(1)、这次抽样调查,一共抽取学生人;(2)、扇形统计图中,扇形E的圆心角度数是;(3)、请补全频率分布直方图;(4)、已知该校七年级共有学生360人,请估计身高在的学生约有多少人?22. 某中学开学初到商场购买A.B两种品牌的足球,购买A种品牌的足球50个,B种品牌的足球25个,共花费4500元.已知购买一个B种品牌的足球比购买一个A种品牌的足球多花30元(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元?(2)、学校为了响应习总书记“足球进校园”的号召,决定再次购进A.B两种品牌足球共50个,正好赶上商场对商品价格进行调整,A品牌足球售价比第一次购买时提高4元,B品牌足球按第一次购买时售价的9折出售,如果学校此次购买A.B两种品牌足球的总费用不超过第一次花费的70%,且保证这次购买的B种品牌足球不少于23个,则这次学校有哪几种购买方案?23. 如图1,已知AB∥CD,∠B=20°,∠D=110°. (1)、若∠E=50°,请直接写出∠F的度数;(2)、探索∠E与∠F之间满足的数量关系,并说明理由;(3)、如图2,EP平分∠BEF,FG平分∠EFD,FG的反向延长线交EP于点P,求∠P的度数.
(1)、若∠E=50°,请直接写出∠F的度数;(2)、探索∠E与∠F之间满足的数量关系,并说明理由;(3)、如图2,EP平分∠BEF,FG平分∠EFD,FG的反向延长线交EP于点P,求∠P的度数.