山西省大同市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-08 类型:期末考试
一、单选题
-
1. 4的算术平方根是A、 B、 C、 D、22. 下列调查适宜采用全面调查方式的是( )A、了解山西省七年级学生的健康状况 B、了解一批灯泡的使用寿命 C、神舟十四号发射前,对各个零部件进行检查 D、了解某品牌的新能源电动汽车的蓄电池的性能3. 已知a>b,则下列不等式成立的是( )A、﹣a>﹣b B、a﹣5<b﹣5 C、2a>2b D、4. 如图,直线AB与CD交于点O,过点O作EO⊥CD,∠AOE=50°,则∠BOC的度数是( )
 A、140° B、135° C、130° D、120°5. 1.第19届亚洲运动会将于2022年9月10日至2022年9月25日在我国浙江省杭州市举行.小明与小亮为了解我国在最近九届亚洲运动会上获得奖牌总数的变化趋势,最适宜选择的统计图是( )
A、140° B、135° C、130° D、120°5. 1.第19届亚洲运动会将于2022年9月10日至2022年9月25日在我国浙江省杭州市举行.小明与小亮为了解我国在最近九届亚洲运动会上获得奖牌总数的变化趋势,最适宜选择的统计图是( ) A、频数分布直方图 B、条形统计图 C、扇形统计图 D、折线统计图6. 下列计算正确的是( )A、 B、 C、 D、7. 将不等式组的解集表示在数轴上,正确的是( )A、
A、频数分布直方图 B、条形统计图 C、扇形统计图 D、折线统计图6. 下列计算正确的是( )A、 B、 C、 D、7. 将不等式组的解集表示在数轴上,正确的是( )A、 B、
B、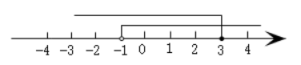 C、
C、 D、
D、 8. 在平面直角坐标系中,点A的坐标是(3a﹣9,a﹣2),则下列说法正确的是( )A、当点A在x轴上时,a=3 B、当点A在y轴上时,a=2 C、当a>3时,点A在第一象限 D、当a<2时,点A在第二象限9. 盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,一服装厂用某种布料生产玩偶A与玩偶B组合成一批盲盒,一个盲盒搭配1个玩偶A和2个玩偶B,已知每米布料可做1个玩偶A或3个玩偶B,现计划用136米这种布料生产这批盲盒(不考虑布料的损耗),设用x米布料做玩偶A,用y米布料做玩偶B,使得恰好配套,则下列方程组正确的是( )A、 B、 C、 D、10. 关于x的不等式x﹣1<a有3个非负整数解,则a的取值范围是( )A、1<a<2 B、1<a≤2 C、1≤a≤2 D、2<a≤3
8. 在平面直角坐标系中,点A的坐标是(3a﹣9,a﹣2),则下列说法正确的是( )A、当点A在x轴上时,a=3 B、当点A在y轴上时,a=2 C、当a>3时,点A在第一象限 D、当a<2时,点A在第二象限9. 盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,一服装厂用某种布料生产玩偶A与玩偶B组合成一批盲盒,一个盲盒搭配1个玩偶A和2个玩偶B,已知每米布料可做1个玩偶A或3个玩偶B,现计划用136米这种布料生产这批盲盒(不考虑布料的损耗),设用x米布料做玩偶A,用y米布料做玩偶B,使得恰好配套,则下列方程组正确的是( )A、 B、 C、 D、10. 关于x的不等式x﹣1<a有3个非负整数解,则a的取值范围是( )A、1<a<2 B、1<a≤2 C、1≤a≤2 D、2<a≤3二、填空题
-
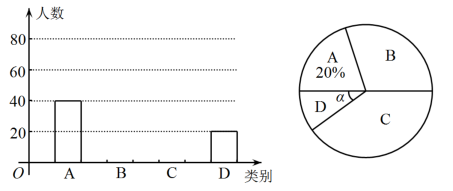
11. 比较大小:5.(填“>”“=”或“<”)12. 已知点A(﹣3,4),B(5,4),则A,B两点间的距离是 .13. 若关于x,y的二元一次方程组的解x,y满足x+y>1,则a的取值范围是 .14. 为促进城市交通更加文明,公共秩序更加优良,很多城市发布“车让人”的倡议,此倡议得到了市民的一致赞赏.为了更好地完善“车让人”的倡议,某市随机抽取了一部分市民对“车让人”的倡议改进意见的支持情况进行了统计,并将统计结果绘制成如图所示的两幅不完整的统计图,则扇形统计图中∠α的度数是 .
“车让人”改进意见
A.加大倡议宣传力度
B.加大罚款力度
C.明确倡议细则
D.增加监控路段
注:每位市民只选择其中一项
 15. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB,CD.若CD∥BE,∠1=42°,则∠2的度数是 .
15. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB,CD.若CD∥BE,∠1=42°,则∠2的度数是 .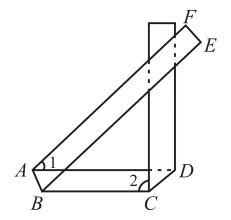
三、解答题
-
16.(1)、计算:;(2)、解二元一次方程组: .17. 下面是小明同学解不等式的过程,请认真阅读并完成相应任务.
解不等式: .
解:去分母,得24﹣(2x﹣7)>3(x+2).
……
(1)、任务一:“去分母”这一步的变形依据是(填“A”或“B”).A.不等式两边乘(或除以)同一个正数,不等号的方向不变
B.不等式两边乘(或除以)同一个负数,不等号的方向改变
(2)、任务二:请完成上述解不等式的余下步骤,并把解集表示在数轴上. 18. 如图,在平面直角坐标系中,三角形ABC的三个顶点都在网格的格点上,其中点C的坐标为(1,2).
18. 如图,在平面直角坐标系中,三角形ABC的三个顶点都在网格的格点上,其中点C的坐标为(1,2).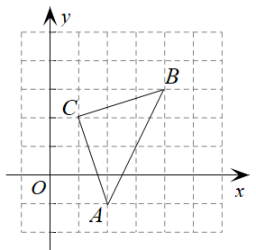 (1)、点A的坐标为 , 点B的坐标为;(2)、将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形A'B'C',请画出平移后的三角形A'B'C',并写出点A',B',C'的坐标.19. 2022年3月23日下午,中国空间站“天宫课堂”再度开课,“太空教师”翟志刚、王亚平、叶光富演示了太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验.某校为了培养学生对航天知识的学习兴趣,组织全校800名学生进行了“航天知识竞赛”.教务处从中随机抽取了部分学生的竞赛成绩,绘制成如下不完整的频数分布表和频数分布直方图:
(1)、点A的坐标为 , 点B的坐标为;(2)、将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形A'B'C',请画出平移后的三角形A'B'C',并写出点A',B',C'的坐标.19. 2022年3月23日下午,中国空间站“天宫课堂”再度开课,“太空教师”翟志刚、王亚平、叶光富演示了太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验.某校为了培养学生对航天知识的学习兴趣,组织全校800名学生进行了“航天知识竞赛”.教务处从中随机抽取了部分学生的竞赛成绩,绘制成如下不完整的频数分布表和频数分布直方图: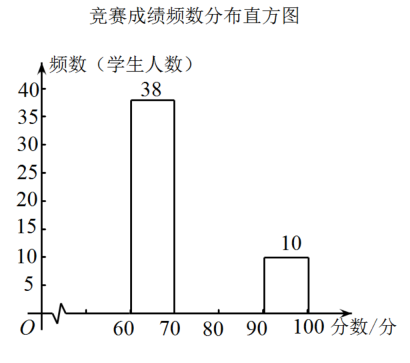
竞赛成绩频数分布表
分数段
频数
百分比
60≤m<70
38
38%
70≤m<80
a
32%
80≤m<90
b
c
90≤m≤100
10
10%
合计
1
请根据以上信息,解答下列问题:
(1)、求频数分布表中a+b的值及c的值;(2)、补全频数分布直方图;(3)、若竞赛成绩为90分以上(含90分)将获得一等奖,请估计全校获得一等奖的人数.20. 阅读下列材料:《张丘建算经》是一部数学问题集,其内容、范围与《九章算术》相仿.其中提出并解决了一个在数学史上非常著名的不定方程问题,通常称为“百鸡问题”:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一,凡百钱买鸡百只,问鸡翁、母、雏各几何.”
译文:公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱,现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?结合你学过的知识,解决下列问题:
(1)、若设公鸡有x只,母鸡有y只,①则小鸡有只,买小鸡一共花费文钱;(用含x,y的式子表示)
②根据题意列出一个含有x,y的方程:;
(2)、若对“百鸡问题”增加一个条件:公鸡数量是母鸡数量的3倍,求此时公鸡、母鸡、小鸡各有多少只?21. 如图,点A,B,C,D在同一条直线上,∠ABF与∠DCE互补,EF∥AD,CF平分∠ACE. (1)、判断BF与CE的位置关系,并说明理由;(2)、若∠CFE=65°,求∠E的度数.22. 某学校配备信息化教室,准备购置甲、乙两种不同型号的电脑,经调查发现,购买3台甲种型号的电脑和7台乙种型号的电脑共需5.3万元,购买6台甲种型号的电脑和5台乙种型号的电脑共需6.1万元.(1)、求甲种型号的电脑和乙种型号的电脑每台的售价分别是多少元.(2)、根据学校的实际情况,需购买甲、乙两种型号的电脑共50台,且购买的总费用不超过27万元.请问最多可以购买甲种型号的电脑多少台?23. 综合与探究
(1)、判断BF与CE的位置关系,并说明理由;(2)、若∠CFE=65°,求∠E的度数.22. 某学校配备信息化教室,准备购置甲、乙两种不同型号的电脑,经调查发现,购买3台甲种型号的电脑和7台乙种型号的电脑共需5.3万元,购买6台甲种型号的电脑和5台乙种型号的电脑共需6.1万元.(1)、求甲种型号的电脑和乙种型号的电脑每台的售价分别是多少元.(2)、根据学校的实际情况,需购买甲、乙两种型号的电脑共50台,且购买的总费用不超过27万元.请问最多可以购买甲种型号的电脑多少台?23. 综合与探究在平面直角坐标系中,点A在第四象限,将线段AO平移至线段BC的位置,点A的对应点是点B,点O的对应点是点C.
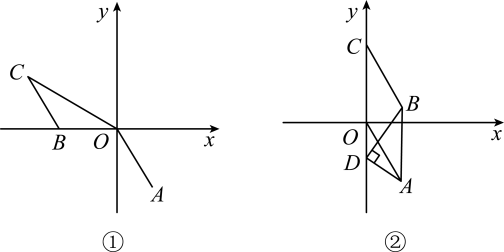 (1)、如图①,点A的坐标是(2,﹣3),点B的坐标是(﹣3,0),连接OC.若在y轴上存在一点P,使得三角形COP的面积是三角形OBC的面积的2倍,求点P的坐标.(2)、如图②,当点C在y轴的正半轴上,点D在y轴的负半轴上,且∠ADB=90°时,试猜想∠CBD与∠OAD的数量关系,并说明理由.
(1)、如图①,点A的坐标是(2,﹣3),点B的坐标是(﹣3,0),连接OC.若在y轴上存在一点P,使得三角形COP的面积是三角形OBC的面积的2倍,求点P的坐标.(2)、如图②,当点C在y轴的正半轴上,点D在y轴的负半轴上,且∠ADB=90°时,试猜想∠CBD与∠OAD的数量关系,并说明理由.