山东省威海市环翠区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-09-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列事件中是必然事件的是（）

A、打开电视机，正在播放《新闻联播》 B、某种彩票中奖概率为1%，买100张该种彩票一定会有一张中奖 C、投掷一枚质地均匀的硬币100次，正面朝上的次数为50次 D、367个同学参加一个集会，他们中至少有两个同学的生日是同月同日

查看试题解析
2. 在 $△ A B C$ 中， $∠ A = 2 ∠ B = 3 ∠ C$ ，则 $△ A B C$ 是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、都有可能

查看试题解析
3. 2022年3月5日，李克强总理在政府工作报告中提出，今年发展主要预期目标之一是粮食产量保持在1.3万亿斤以上．若用x（万亿斤）表示我国今年粮食产量，则x满足的关系为（）

A、 $x \geq 1.3$ B、 $x > 1.3$ C、 $x \leq 1.3$ D、 $x < 1.3$

查看试题解析
4. 图，点 $A$ ， $B$ ， $E$ 共线，下列条件中不能判断 $A D ∥ B C$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ A = ∠ 5$ C、 $∠ 3 = ∠ 4$ D、 $∠ A + ∠ A B C = 180 °$

查看试题解析
5. 已知直线 $y = - 2 x$ 与 $y = k x + b$ 交点的坐标为 $(a ， 2)$ ，则方程组 ${\begin{array}{l} 2 x + y = 0 \\ k x + b - y = 0 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ C、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = - 2 \end{array}$

查看试题解析
6. 如图，A、B是边长为1的小正方形组成的网格上的两个格点，在其余的格点中任意放置点C，恰好能使△ABC构成等腰三角形的概率是（）

A、 $\frac{6}{23}$ B、 $\frac{1}{5}$ C、 $\frac{9}{23}$ D、 $\frac{7}{25}$

查看试题解析
7. 若 $m > n$ ，则下列各式中正确的是（）

A、 $m^{2} > n^{2}$ B、 $m + 1 > n - 1$ C、 $m^{2} + 1 > n^{2} - 1$ D、 $m - 1 > n + 1$

查看试题解析
8. 如图，在 $△ A B C$ 和 $△ C D E$ 中， $∠ A C B = ∠ C E D = 90 ° ， A B = C D ， C E = A C$ ，则下列结论中错误的是（）

A、 $△ A B C ≌ △ C D E$ B、 $∠ C A B = ∠ D C E$ C、 $A B ⊥ C D$ D、E为BC中点

查看试题解析
9. 某山西特产专卖店有一款老陈醋进价为每盒100元，标价为150元，现准备打折销售，若要保证利润率不少于5%，最多可以按几折销售？设按x折销售，根据题意可列不等式（）

A、 $150 x - 100 \geq 5 % \times 100$ B、 $150 \times \frac{1}{10} x - 100 \leq 5 % \times 100$ C、 $150 \times \frac{1}{10} x - 100 \geq 5 % \times 100$ D、 $150 \times \frac{1}{10} x - 100 > 5 % \times 150$

查看试题解析
10. 一副三角板如图所示摆放，若 $∠ 1 = 85 °$ ，则 $∠ 2$ 的度数是（）

A、85° B、95° C、100° D、105°

查看试题解析
11. 被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作．《九章算术》中记载：“今有五雀、六燕，集称之衡，雀俱重，燕俱轻．一雀一燕交而处，衡适平．并燕、雀重一斤．问燕、雀一枚各重几何？”译文：“今有5只雀、6只燕，分别聚集而且用衡器称之，聚在一起的雀重，燕轻．将一只雀、一只燕交换位置而放，重量相等.5只雀、6只燕重量为1斤．问雀、燕每只各重多少斤？”设每只雀重x斤，每只燕重y斤，可列方程组为（）

A、 ${\begin{array}{l} 5 x + y = 4 y + x \\ 5 x - 6 y = 1 \end{array}$ B、 ${\begin{array}{l} 4 x + y = 5 y + x \\ 5 x + 6 y = 1 \end{array}$ C、 ${\begin{array}{l} 5 x + y = 4 y + x \\ 5 x + 6 y = 1 \end{array}$ D、 ${\begin{array}{l} 4 x + y = 5 y + x \\ 5 x - 6 y = 1 \end{array}$

查看试题解析
12. 如图，在平面直角坐标系xOy中，若直线 $y_{1} = - x + a$ 与直线 $y_{2} = b x - 4$ 相交于点P，则下列结论中：
① $a < b$ ；
②当 $0 < x < 1$ 时， $y_{2} < y_{1} < 0$ ；
③关于x，y的方程组 ${\begin{array}{l} y = - x + a \\ y = b x - 4 \end{array}$ 的解是 ${\begin{array}{l} x = 1 \\ y = - 3 \end{array}$ ；
所有正确结论的序号是（）

A、①② B、②③ C、①③ D、①②③

查看试题解析

二、填空题

13. 在一个不透明的盒子里装有3个黑球和若干个白球，它们除颜色外都相同，搅匀后从中任意摸出一个球记下颜色再把它放回盒子中、不断重复实验，统计结果显示，随着实验次数越来越大，摸到黑球的频率逐渐稳定在0.25左右，则据此估计盒子中大约有白球个．

查看试题解析
14. 如图，AB∥EF，设∠C＝90°，那么x，y，z的关系式为.

查看试题解析
15. 已知不等式组 ${\begin{array}{l} x < 2 x + 1 \\ x - m > 1 \end{array}$ 的解集为 $x > - 1$ ，则m的取值范围是．

查看试题解析
16. 小明在解二元一次方程组 ${\begin{array}{l} x - y = 4 \\ * x + y = 8 \end{array}$ 时，发现系数“*”印刷不清楚．数学老师说：“我知道本题标准答案的结果中的x和y是一对相反数” ．原题中的“*”所指的系数为．

查看试题解析
17. $Δ A B C$ 中，AB＝AC， $A B$ 的中垂线与 $A C$ 所在直线相交成的锐角为 $50 °$ ，则底角 $B$ 的大小为．

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ C = 90 ° ， A D$ 平分 $∠ B A C$ 交 $B C$ 于点D， $D E$ // $A B$ 交 $A C$ 于点E，已知 $C E = 3 ， C D = 4$ ，则 $A D$ 长为．

查看试题解析

三、解答题

19. 计算：

(1)、解方程组 ${\begin{array}{l} \frac{x}{3} - \frac{y}{4} = 1 \\ 3 x - 4 y = 2 \end{array}$

(2)、解不等式组，并将解集在数轴上表示出来．
${\begin{array}{l} x - 1 < \frac{1 + 2 x}{3} \\ x - 3 (x - 2) \geq 4 \end{array}$

查看试题解析
20. 如图， $A B = C D$ ， $A E ⊥ B C$ 于E， $D F ⊥ B C$ 于F，且 $B F = C E$ ．判断AE和DF的关系，并说明理由．

查看试题解析
21. 按要求设计方案：

(1)、设计一个转盘，使转盘停止转动时，“指针落在黑色区域”与“指针落在白色区域”出现的可能性一样大；

(2)、在一个小正方体的6个面上分别写上一个数字，抛掷这个小正方体，使“向上一面的数字为2”比“向上一面的数字为3”出现的可能性大．

查看试题解析
22. 已知 $△ A O B$ 和 $△ M O N$ 都是等腰直角三角形， $∠ A O B = ∠ M O N = 90 °$ ．

(1)、如图1，连接 $A M$ ， $B N$ ，求证： $△ A O M$ 和 $△ B O N$ 全等：

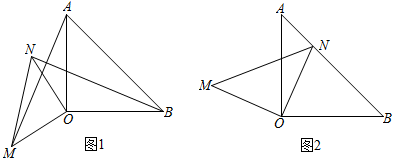(2)、如图2，将 $△ M O N$ 绕点O顺时针旋转，当点N恰好在 $A B$ 边上时，求证： $B N^{2} + A N^{2} = 2 O N^{2}$ ．

查看试题解析
23. 某公司每月付给销售人员的工资有两种方案．
方案一：没有底薪，只拿销售提成；
方案二：底薪加销售提成．
设x（件）是销售商品的数量，y（元）是销售人员的月工资，如图所示，h为方案一的函数图象， $l_{2}$ 为方案二的函数图象，已知每件商品的销售提成方案二比方案一少20元，根据图中信息解答如下问题（注：销售提成是指从销售每件商品得到的销售额中提取一定数量的费用）；

(1)、求 $l_{1}$ 的表达式；

(2)、请问方案二中每月（按30天计）付给销售人员的底薪是多少元？

(3)、如果你是该公司销售人员，你认为应该选择怎样的薪金方案？

查看试题解析

24. 5G时代的到来，将给人类生活带来巨大改变.现有A、B两种型号的5G手机，进价和售价如表所示：

价格型号	进价（元/部）	售价（元/部）
A	3000	3400
B	3500	4000

某营业厅购进A、B两种型号手机共花费32000元，手机销售完成后共获得利润4400元.

(1)、营业厅购进A、B两种型号手机各多少部？

(2)、若营业厅再次购进A、B两种型号手机共20部，其中B型手机的数量不多于A型手机数量的2倍，请设计一个方案：营业厅购进两种型号手机各多少部时获得最大利润，最大利润是多少？

查看试题解析

25. 如图，直线 $y = - \frac{4}{3} x + 4$ 与x轴和y轴分别交于A、B两点，把射线AB绕点A顺时针旋转90°得射线AC，点P是射线AC上一个动点，点Q是x轴上一个动点．若 $△ P Q A$ 与 $△ A O B$ 全等，试确定点Q的横坐标．

查看试题解析