山东省泰安市新泰市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-08 类型:期末考试
一、单选题
-
1. 不等式的解集是( )A、x< B、x<-1 C、x> D、x>-12. 如图,直线 , 则等于( )
 A、 B、 C、 D、3. 如图,若AB,CD相交于点E,若 , , 则的度数是( )
A、 B、 C、 D、3. 如图,若AB,CD相交于点E,若 , , 则的度数是( ) A、48° B、62° C、76° D、88°4. 一元一次不等式组 的解集在数轴上表示为( ).A、
A、48° B、62° C、76° D、88°4. 一元一次不等式组 的解集在数轴上表示为( ).A、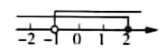 B、
B、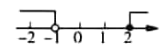 C、
C、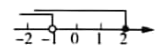 D、
D、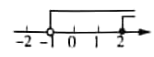 5. 如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,事件“指针所落扇形中的数大于3”的概率为( )
5. 如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,事件“指针所落扇形中的数大于3”的概率为( ) A、 B、 C、 D、6. 如图,在等边三角形ABC中,BC=2,D是AB的中点,过点D作DF⊥AC于点F,过点F作EF⊥BC于点E,则BE的长为( )
A、 B、 C、 D、6. 如图,在等边三角形ABC中,BC=2,D是AB的中点,过点D作DF⊥AC于点F,过点F作EF⊥BC于点E,则BE的长为( ) A、1 B、 C、 D、7. 下列关于命题“若 ,则 ”的说法,正确的是( )A、是真命题 B、是假命题,反例是“ ” C、是假命题,反例是“ ” D、是假命题,反例是“ ”8. 已知关于x,y的方程是二元一次方程,则m,n的值为( )A、 B、 C、 D、9. 如图,在中, , AE是的平分线,外角 , 则的度数为( )
A、1 B、 C、 D、7. 下列关于命题“若 ,则 ”的说法,正确的是( )A、是真命题 B、是假命题,反例是“ ” C、是假命题,反例是“ ” D、是假命题,反例是“ ”8. 已知关于x,y的方程是二元一次方程,则m,n的值为( )A、 B、 C、 D、9. 如图,在中, , AE是的平分线,外角 , 则的度数为( ) A、65° B、70° C、75° D、50°10. 我国古典数学文献《增删算法统宗·六均输》中有一个“隔沟计算”的问题:“甲乙隔沟牧放,二人暗里参详.甲云得乙九只羊,多乙一倍之上.乙说得甲九只,两家之数相当.二人闲坐恼心肠,画地算了半晌.”翻译成现代文,其大意如下:甲乙两人隔一条沟放牧,二人心里暗中合计.甲对乙说:“我得到你的九只羊,我的羊就比你多一倍.”乙对甲说:“我得到你的九只羊,咱俩家的羊一样多.”两个人在沟两边闲坐,心里很烦躁,因为在地上画了半晌,也没算出来.请问甲乙各有多少只羊呢?设甲有羊x只,乙有羊y只,则正确的方程组是( )A、 B、 C、 D、11. 如图, , 平分 . 下列说法错误的是( )
A、65° B、70° C、75° D、50°10. 我国古典数学文献《增删算法统宗·六均输》中有一个“隔沟计算”的问题:“甲乙隔沟牧放,二人暗里参详.甲云得乙九只羊,多乙一倍之上.乙说得甲九只,两家之数相当.二人闲坐恼心肠,画地算了半晌.”翻译成现代文,其大意如下:甲乙两人隔一条沟放牧,二人心里暗中合计.甲对乙说:“我得到你的九只羊,我的羊就比你多一倍.”乙对甲说:“我得到你的九只羊,咱俩家的羊一样多.”两个人在沟两边闲坐,心里很烦躁,因为在地上画了半晌,也没算出来.请问甲乙各有多少只羊呢?设甲有羊x只,乙有羊y只,则正确的方程组是( )A、 B、 C、 D、11. 如图, , 平分 . 下列说法错误的是( ) A、 B、 C、 D、12. 如图,在中, , , , 以点A为圆心,以AB的长为半径作弧交AC于点D,连接BD,再分别以点B,D为圆心,大于的长为半径作弧,两弧交于点P,作射线AP交BC于点E,连接DE,则下列结论:①;②DE垂直平分线段AC;③;④ . 其中正确的个数是( )
A、 B、 C、 D、12. 如图,在中, , , , 以点A为圆心,以AB的长为半径作弧交AC于点D,连接BD,再分别以点B,D为圆心,大于的长为半径作弧,两弧交于点P,作射线AP交BC于点E,连接DE,则下列结论:①;②DE垂直平分线段AC;③;④ . 其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是 .
 14. 如图, , 若 , , 则的度数为 .
14. 如图, , 若 , , 则的度数为 .
 15. 若不等式组无解,则m的取值范围是 .16. 如图,AE,CE分别平分和 , , , 则 .
15. 若不等式组无解,则m的取值范围是 .16. 如图,AE,CE分别平分和 , , , 则 . 17. 淇淇的爸爸骑摩托车载着淇淇在公路上匀速行驶,在12:00点时,淇淇看到路边里程碑上的数是一个两位数,它的两个数字之和为7,在13:00点时看到路边里程碑上的数仍然是一个两位数,但十位与个位数字与12:00点时看到的正好互换了,在14:00点时看到的数比12:00点时看到的两位数中间多了个0.则淇淇在14:00点时看到路边里程碑上的数为 .18. 如图,一次函数与的图象交于点P.下列结论:①;②;③;④关于x的不等式的解集为 . 其中所有正确结论的序号是 .
17. 淇淇的爸爸骑摩托车载着淇淇在公路上匀速行驶,在12:00点时,淇淇看到路边里程碑上的数是一个两位数,它的两个数字之和为7,在13:00点时看到路边里程碑上的数仍然是一个两位数,但十位与个位数字与12:00点时看到的正好互换了,在14:00点时看到的数比12:00点时看到的两位数中间多了个0.则淇淇在14:00点时看到路边里程碑上的数为 .18. 如图,一次函数与的图象交于点P.下列结论:①;②;③;④关于x的不等式的解集为 . 其中所有正确结论的序号是 .
三、解答题
-
19. 解方程组:(1)、;(2)、 .20. 求不等式组
的整数解.
21. 口袋里有除颜色外其它都相同的6个红球和4个白球.(1)、先从袋子里取出m()个白球,再从袋子里随机摸出一个球,将“摸出红球”记为事件A.①如果事件A是必然事件,请直接写出m的值.
②如果事件A是随机事件,请直接写出m的值.
(2)、先从袋子中取出m个白球,再放入m个一样的红球并摇匀,摸出一个球是红球的可能性大小是 , 求m的值.22. 如图,在中,AD平分 , 过点B作AD的垂线,垂足为点D, , 交AB于点E, . (1)、求证:是等腰三角形;(2)、求证: .23. 已知: .
(1)、求证:是等腰三角形;(2)、求证: .23. 已知: .
 (1)、如图1,求证:;(2)、如图2,点F在AB、CD之间, , AG平分交CD于点G,若 , , 求的大小.24. 在2022北京冬奥会期间,某商场共用3200元的总进货款购进A、B两种水果各400斤,已知购进A水果3斤与购进B水果5斤的进货款相同.(1)、求该商场购进每斤A、B水果的进货价格各是多少元?(2)、若该商场把购进的这些A、B水果的一部分均按每斤6元的定价进行零售;把另一部分水果均按4元的定价进行零售.在全部售出的情况下,若依靠购进的这些水果所得的利润不低于1000元,则按每斤6元定价的水果至少多少斤?25. 如图,在中, , CD,BE是的高,点F为BC中点,点E在AC上,BE与DF,DC分别交于点G,H.
(1)、如图1,求证:;(2)、如图2,点F在AB、CD之间, , AG平分交CD于点G,若 , , 求的大小.24. 在2022北京冬奥会期间,某商场共用3200元的总进货款购进A、B两种水果各400斤,已知购进A水果3斤与购进B水果5斤的进货款相同.(1)、求该商场购进每斤A、B水果的进货价格各是多少元?(2)、若该商场把购进的这些A、B水果的一部分均按每斤6元的定价进行零售;把另一部分水果均按4元的定价进行零售.在全部售出的情况下,若依靠购进的这些水果所得的利润不低于1000元,则按每斤6元定价的水果至少多少斤?25. 如图,在中, , CD,BE是的高,点F为BC中点,点E在AC上,BE与DF,DC分别交于点G,H.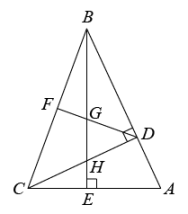 (1)、求证:;(2)、若 , , 求 .
(1)、求证:;(2)、若 , , 求 .