山东省泰安市宁阳县2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-08 类型:期末考试
一、单选题
-
1. 下列各组数值中,是二元一次方程的一个解的是( )A、 B、 C、 D、2. 若x>y , 则下列不等式不一定成立的是( )A、x+1>y+1 B、2x>2y C、 > D、x2>y23. 下列命题是假命题的是( )A、所有的实数都可以用数轴上的点来表示 B、在直角三角形中,如果一个锐角等于 , 那么它所对的直角边等于斜边的一半 C、斜边和一条直角边分别相等的两个直角三角形全等 D、三角形的一个外角一定大于三角形的内角4. 将含30°角的一个直角三角板和一把直尺如图放置,若 , 则等于( )
 A、80° B、100° C、110° D、120°5. 如图,在△ABC和△ADE中,已知AB=AD,还需要添加两个条件,才能使△ABC≌△ADE,不能添加的一组是( )
A、80° B、100° C、110° D、120°5. 如图,在△ABC和△ADE中,已知AB=AD,还需要添加两个条件,才能使△ABC≌△ADE,不能添加的一组是( ) A、BC=DE,AC=AE B、∠B=∠D,∠BAC=∠DAE C、BC=DE,∠C=∠E D、AC=AE,∠BAD=∠CAE6. 如图,下列哪种说法错误( )
A、BC=DE,AC=AE B、∠B=∠D,∠BAC=∠DAE C、BC=DE,∠C=∠E D、AC=AE,∠BAD=∠CAE6. 如图,下列哪种说法错误( ) A、 B、 C、 D、7. 如图,在中,的垂直平分线交于点 , 交于点 , 连接 . 若 , , 则的周长为( )
A、 B、 C、 D、7. 如图,在中,的垂直平分线交于点 , 交于点 , 连接 . 若 , , 则的周长为( ) A、8 B、11 C、16 D、178. 不等式组的解集在数轴上表示为( )A、
A、8 B、11 C、16 D、178. 不等式组的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 9. 不等式组 的解集为 ,则 的取值范围为( )A、 B、 C、 D、10. 如图,经过点和经过原点和点 , 以两条直线的交点坐标为解的方程组是( )
9. 不等式组 的解集为 ,则 的取值范围为( )A、 B、 C、 D、10. 如图,经过点和经过原点和点 , 以两条直线的交点坐标为解的方程组是( ) A、 B、 C、 D、11. 如图,直线y=kx+b(k,b是常数,k≠0)与直线y=2交于点A(4,2),则关于x的不等式kx+b<2的解集为( )
A、 B、 C、 D、11. 如图,直线y=kx+b(k,b是常数,k≠0)与直线y=2交于点A(4,2),则关于x的不等式kx+b<2的解集为( ) A、x<4 B、x≤4 C、x>4 D、x>212. 如图,和是两个等边三角形,是以为斜边的等腰直角三角形,连接 , , , 下列三个结论:①;②;③点在线段的中垂线上;④;⑤;⑥ . 其中正确的结论的个数是( )
A、x<4 B、x≤4 C、x>4 D、x>212. 如图,和是两个等边三角形,是以为斜边的等腰直角三角形,连接 , , , 下列三个结论:①;②;③点在线段的中垂线上;④;⑤;⑥ . 其中正确的结论的个数是( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
13. 长度为3,7,的三条线段可以围成一个三角形,则的取值范围为 .14. 长度分别为3cm,4cm,5cm,9cm的四条线段,任取其中三条能组成三角形的概率是 .15. 如图,AD是等边三角形ABC的中线,AE=AD,则∠EDC= .
 16. 若等腰三角形的底角为15°,腰长为2a,则腰的高为 .17. 如图,在中 , 的垂直平分线交于 , 交的延长线于 , 若 , , 则的长是 .
16. 若等腰三角形的底角为15°,腰长为2a,则腰的高为 .17. 如图,在中 , 的垂直平分线交于 , 交的延长线于 , 若 , , 则的长是 . 18. 如图,已知∠MON=30点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …均为等边三角形,若OA1=1,则△A2021B2021A2022的边长为 .
18. 如图,已知∠MON=30点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …均为等边三角形,若OA1=1,则△A2021B2021A2022的边长为 .
三、解答题
-
19. 计算(1)、解方程组:(2)、解方程组:(3)、解不等式:(4)、已知关于 , 的二元一次方程组的解满足 , 求的取值范围.20. 一只口袋里放着个红球、个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀.(1)、取出红球的概率为 , 白球有多少个?(2)、取出黑球的概率是多少?(3)、再在原来的袋中放进多少个红球,能使取出红球的概率达到?21. 某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x的函数关系如图所示,解答下列问题
 (1)、分别求出选择这两种卡消费时,y关于x的函数表达式;(2)、请根据入园次数确定选择哪种卡消费比较合算.22. 如图,在中,的平分线交于点 , 过点作;交于点 .
(1)、分别求出选择这两种卡消费时,y关于x的函数表达式;(2)、请根据入园次数确定选择哪种卡消费比较合算.22. 如图,在中,的平分线交于点 , 过点作;交于点 .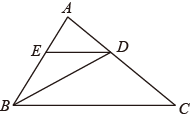 (1)、求证:;(2)、若 , 求的度数.23. 如图,在中, , , 是的角平分线, , 垂足为.
(1)、求证:;(2)、若 , 求的度数.23. 如图,在中, , , 是的角平分线, , 垂足为. (1)、已知 , 求的长.(2)、求证:.24. 快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)、已知 , 求的长.(2)、求证:.24. 快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)、求甲、乙两种型号的机器人每台的价格各是多少万元;(2)、已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
25. 如图,中,于点 , , 为上一点,且 , 连接并延长交于点 .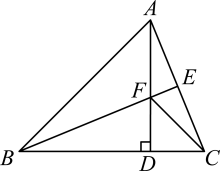 (1)、求证: , ;(2)、连接 , 若 .
(1)、求证: , ;(2)、连接 , 若 .①求证:;
②若 , 求的长.