山东省济南市长清区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-08 类型:期末考试
一、单选题
-
1. 2022年北京和张家口成功举办了第24届冬奥会和冬残奥会.下面关于奥运会的剪纸图片中是轴对称图形的是( )A、
 B、
C、
B、
C、 D、
D、 2. 将数据0.00000105用科学记数法表示为( )A、10.5×10-7 B、1.05×10-7 C、 D、0.105×10-53. 一个小球在如图所示的方格地板上自由滚动,并随机停留在某块地板上,每块地板大小、质地完全相同,那么该小球停留在黑色区域的概率是( )
2. 将数据0.00000105用科学记数法表示为( )A、10.5×10-7 B、1.05×10-7 C、 D、0.105×10-53. 一个小球在如图所示的方格地板上自由滚动,并随机停留在某块地板上,每块地板大小、质地完全相同,那么该小球停留在黑色区域的概率是( ) A、 B、 C、 D、4. 如图,ABCD,AD⊥AC,∠BAD=35°,则∠ACD=( )
A、 B、 C、 D、4. 如图,ABCD,AD⊥AC,∠BAD=35°,则∠ACD=( ) A、35° B、45° C、55° D、70°5. 下列运算正确的是( )A、(﹣2a3)2=4a6 B、a2•a3=a6 C、3a+a2=3a3 D、(a﹣b)2=a2﹣b26. 小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系( )A、
A、35° B、45° C、55° D、70°5. 下列运算正确的是( )A、(﹣2a3)2=4a6 B、a2•a3=a6 C、3a+a2=3a3 D、(a﹣b)2=a2﹣b26. 小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分)之间的关系( )A、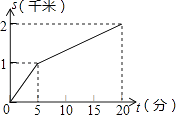 B、
B、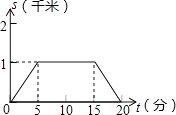 C、
C、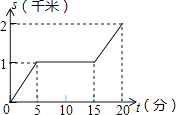 D、
D、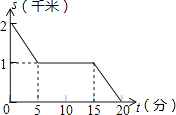 7. 在△ABC与△DFE中,∠B=∠F,AB=DF,∠A=∠D,能得到△ABC≌△DFE的方法是( )
7. 在△ABC与△DFE中,∠B=∠F,AB=DF,∠A=∠D,能得到△ABC≌△DFE的方法是( ) A、SSS B、SAS C、ASA D、AAS8. 如图,有一个圆柱,它的高等于9cm,底面上圆的周长等于24cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面与点A相对的点B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程是( )
A、SSS B、SAS C、ASA D、AAS8. 如图,有一个圆柱,它的高等于9cm,底面上圆的周长等于24cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面与点A相对的点B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程是( ) A、15cm B、17cm C、18cm D、20cm9. 小明做“用频率估计概率”的实验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( )
A、15cm B、17cm C、18cm D、20cm9. 小明做“用频率估计概率”的实验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( ) A、抛掷一枚硬币,落地后硬币正面朝上 B、一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃 C、抛一个质地均匀的正方体骰子,朝上的面点数是3 D、在“石头、剪刀、布”的游戏中,小刚随机出的是“石头”10. 如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中∠AEB=90°,AB=13cm,BE=5cm,则阴影部分的面积是( )
A、抛掷一枚硬币,落地后硬币正面朝上 B、一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃 C、抛一个质地均匀的正方体骰子,朝上的面点数是3 D、在“石头、剪刀、布”的游戏中,小刚随机出的是“石头”10. 如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中∠AEB=90°,AB=13cm,BE=5cm,则阴影部分的面积是( ) A、169cm2 B、25cm2 C、49cm2 D、64cm211. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN长为半径西弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,AB=10,则△ABE的面积是( )
A、169cm2 B、25cm2 C、49cm2 D、64cm211. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN长为半径西弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,AB=10,则△ABE的面积是( ) A、8 B、15 C、24 D、3012. 如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,AD=4,则CH的长为( )
A、8 B、15 C、24 D、3012. 如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,AD=4,则CH的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. (-x)3÷x2=;14. 在一个不透明的袋子里装有红球、黄球共16个,这些球除颜色外都相同,小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是;15. 小玲要求△ABC最长边上的高,测得AB=8cm,AC=6cm,BC=10cm,则最长边上的高为cm.16. 如图,在△ABC中,线段AB的垂直平分线与AC相交于点D,连接BD,边AC的长为12cm,边BC的长为7cm,则△BCD的周长为 cm;
 17. 某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中、分别表示去年、今年水费(元)与用水量()之间的关系.小雨家去年用水量为150 , 若今年用水量与去年相同,水费将比去年多元.
17. 某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中、分别表示去年、今年水费(元)与用水量()之间的关系.小雨家去年用水量为150 , 若今年用水量与去年相同,水费将比去年多元.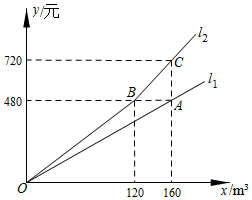 18. 如图,在△ABC中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点,若BC=4,△ABC面积为12,则BM+MD长度的最小值为 .
18. 如图,在△ABC中,AB=AC,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,作直线EF,D为BC的中点,M为直线EF上任意一点,若BC=4,△ABC面积为12,则BM+MD长度的最小值为 .
三、解答题
-
19. 计算:(1)、│-2│+(π-1)0-()-1+(-1)2022;(2)、(x+4)2-(x+2)(x-5)20. 先化简再求值:其中a= , b=﹣2.21. 如图,在边长为1的小正方形所组成的网格上,每个小正方形的顶点都称为“格点”,△ABC的顶点都在格点上,用直尺完成下列作图:
 (1)、作出△ABC关于直线MN的对称图形;(2)、求△ABC的面积;(3)、在直线MN上取一点P,使得AP+CP最小(保留作图痕迹)22. 如图,已知点C、点D都在线段AF上,AC=DF,BC∥EF,∠B=∠E.
(1)、作出△ABC关于直线MN的对称图形;(2)、求△ABC的面积;(3)、在直线MN上取一点P,使得AP+CP最小(保留作图痕迹)22. 如图,已知点C、点D都在线段AF上,AC=DF,BC∥EF,∠B=∠E.求证:
 (1)、△ABC≌△DEF;(2)、ABDE.23. 如图,现有一个圆形转盘被平均分成6等份,分别标有2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
(1)、△ABC≌△DEF;(2)、ABDE.23. 如图,现有一个圆形转盘被平均分成6等份,分别标有2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字. (1)、转到数字9是 , 转到数字6是 , (从“随机事件”、“必然事件”、“不可能事件”选一个填入)(2)、转动转盘一次,转出的数字是3的倍数的概率是多少?(3)、现有两张分别写有2和5的卡片,随机转动转盘一次,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度(长度单位均是厘米),这三条线段能构成三角形的概率是多少?24. 如图,一摞相同规格的碗整齐地叠放在桌面上,请根据表中给出的数据信息,解答问题:
(1)、转到数字9是 , 转到数字6是 , (从“随机事件”、“必然事件”、“不可能事件”选一个填入)(2)、转动转盘一次,转出的数字是3的倍数的概率是多少?(3)、现有两张分别写有2和5的卡片,随机转动转盘一次,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度(长度单位均是厘米),这三条线段能构成三角形的概率是多少?24. 如图,一摞相同规格的碗整齐地叠放在桌面上,请根据表中给出的数据信息,解答问题: (1)、请将下表补充完整:
(1)、请将下表补充完整:碗的数量x(个)
1
2
3
4
5
…
高度y(cm)
4
5.2
7.6
…
(2)、写出整齐叠放在桌面上碗的高度y(cm)与碗的数量x(个)之间的关系式;当碗的数量为10个时,碗的高度是cm;(3)、若这摞碗的高度为20.8cm,求这摞碗的数量.25. 长清的园博园广场视野开阔,阻挡物少,成为不少市民放风筝的最佳场所,某校七年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为15米;②根据手中剩余线的长度计算出风筝线BC的长为25米;③牵线放风筝的小明的身高为1.6米. (1)、求风筝的垂直高度CE;(2)、如果小明想风筝沿CD方向下降12米,则他应该往回收线多少米?26. 问题发现:如图1,如果△ACB和△CDE均为等边三角形,点A、D、E在同一直线上,连接BE.
(1)、求风筝的垂直高度CE;(2)、如果小明想风筝沿CD方向下降12米,则他应该往回收线多少米?26. 问题发现:如图1,如果△ACB和△CDE均为等边三角形,点A、D、E在同一直线上,连接BE. (1)、如图1,请直接写出AD与BE的数量关系为;(2)、如图1,求∠AEB的度数;(3)、拓展:如图2,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?
(1)、如图1,请直接写出AD与BE的数量关系为;(2)、如图1,求∠AEB的度数;(3)、拓展:如图2,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?学生经过讨论,探究出以下解决问题的思路:
思路一:延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,等量代换得到AC=BC+CD.
思路二:将△ABC绕着点A逆时针旋转60°至△ADF,从而容易证明△ACF是等边三角形,故AC=CF,等量代换得到AC=BC+CD.
请选择一种思路,作出图形并写出证明过程.
27. 如图(1),AB=9cm,AC⊥AB,BD⊥AB,AC=BD=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,它们运动的时间为t(s). (1)、若点Q的运动速度为1cm/s,用含t的代数式表示△BPQ的面积;(2)、若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由;(3)、如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=α”,其他条件不变,设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值,若不存在,请说明理由.
(1)、若点Q的运动速度为1cm/s,用含t的代数式表示△BPQ的面积;(2)、若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由;(3)、如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=α”,其他条件不变,设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值,若不存在,请说明理由.