山东省济南市章丘区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-08 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 世界最大的单口径球面射电望远镜被誉为“中国天眼”,在其新发现的脉冲星中有一颗毫秒脉冲星的自转周期为0.00519秒.数据0.00519用科学记数法可以表示为( )A、5.19×10﹣3 B、5.19×10﹣4 C、5.19×10﹣5 D、5.19×10﹣63. 下列事件为必然事件的是( )A、打开电视机,它正在播广告 B、抛掷一枚硬币,一定正面朝上 C、投掷一枚普通的正方体骰子,掷得的点数小于7 D、某彩票的中奖机会是1%,买1张一定不会中奖4. “致中和,天地位焉,万物育焉”,对称美是我国古人和谐平衡思想的体现,常被运用于建筑、器物、绘画、标识等作品的设计上,使对称之美惊艳了千年的时光,在下列标识或简图中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下列能用平方差公式计算的是( )A、 B、 C、 D、6. 如图,直线AD∥BC,若∠1=40°,∠BAC=80°,则∠2的度数为( )
5. 下列能用平方差公式计算的是( )A、 B、 C、 D、6. 如图,直线AD∥BC,若∠1=40°,∠BAC=80°,则∠2的度数为( )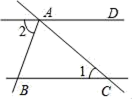 A、70° B、60° C、50° D、40°7. 如图,若∠1=∠3,则下列结论一定成立的是( )
A、70° B、60° C、50° D、40°7. 如图,若∠1=∠3,则下列结论一定成立的是( ) A、∠1=∠4 B、∠3=∠4 C、∠1+∠2=180° D、∠2+∠4=180°8. 如图,点E,点F在直线AC上, AE=CF, AD=CB,下列条件中不能判断△ADF≌△CBE的是( )
A、∠1=∠4 B、∠3=∠4 C、∠1+∠2=180° D、∠2+∠4=180°8. 如图,点E,点F在直线AC上, AE=CF, AD=CB,下列条件中不能判断△ADF≌△CBE的是( ) A、AD//BC B、BE//DF C、BE=DF D、∠A=∠C9. 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率是( )
A、AD//BC B、BE//DF C、BE=DF D、∠A=∠C9. 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率是( ) A、 B、 C、 D、10. 如图,在中, , , , , 是的角平分线, , 垂足为 , 则的周长为( )
A、 B、 C、 D、10. 如图,在中, , , , , 是的角平分线, , 垂足为 , 则的周长为( )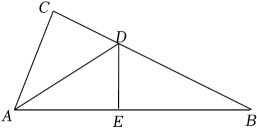 A、23 B、24 C、25 D、3211. 尺规作图作的平分线方法如下:以为圆心,任意长为半径画弧交、于、 , 再分别以点、为圆心,以大于长为半径画弧,两弧交于点 , 作射线由作法得的根据是( )
A、23 B、24 C、25 D、3211. 尺规作图作的平分线方法如下:以为圆心,任意长为半径画弧交、于、 , 再分别以点、为圆心,以大于长为半径画弧,两弧交于点 , 作射线由作法得的根据是( ) A、SAS B、ASA C、AAS D、SSS12. 如图,在边长为2的正方形中,点、分别是边和的中点,点为正方形中心,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止(不含点和点),则的面积随着时间变化的函数图象大致是( )
A、SAS B、ASA C、AAS D、SSS12. 如图,在边长为2的正方形中,点、分别是边和的中点,点为正方形中心,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止(不含点和点),则的面积随着时间变化的函数图象大致是( ) A、
A、 B、
B、 C、
C、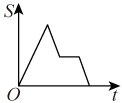 D、
D、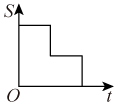
二、填空题
-
13. 计算:的结果等于 .14. 等腰三角形的一边长为 , 另一边长为 , 则该等腰三角形的周长为 .15. 若多项式是完全平方式,则m的值为 .16. 某校九年级共有50名学生参加社区垃圾分类志愿者服务活动,其中男生有30名,女生有20名,若从中随机抽一名学生,恰好抽到男生的概率是 .17. 如图,把一张长方形纸片沿折叠,若 , 则的度数为 .
 18. 如图,△ABD与△ACE都是等边三角形,且AB≠AC,下列结论:①BE=CD;②∠BOD=60°;③∠BDO=∠CEO;④若∠BAC=90°,DA∥BC,则BC⊥EC.其中正确的是 (填序号).
18. 如图,△ABD与△ACE都是等边三角形,且AB≠AC,下列结论:①BE=CD;②∠BOD=60°;③∠BDO=∠CEO;④若∠BAC=90°,DA∥BC,则BC⊥EC.其中正确的是 (填序号).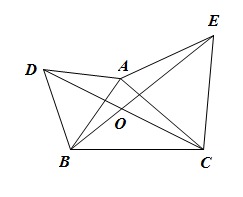
三、解答题
-
19. 计算:(1)、(2)、20. 先化简,再求值: , 其中 , .21. 如图,在正方形网格中,是格点三角形.
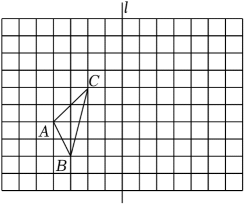 (1)、画出 , 使得和关于直线对称;(2)、请在直线上找一点(即画出点),使点到点和点的距离之和最小;(3)、求的面积.22. 如图所示,点 , 分别在 , 上, , 均与相交, , , 求证: .
(1)、画出 , 使得和关于直线对称;(2)、请在直线上找一点(即画出点),使点到点和点的距离之和最小;(3)、求的面积.22. 如图所示,点 , 分别在 , 上, , 均与相交, , , 求证: . 23. 如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
23. 如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.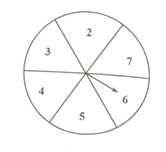
求:
(1)、转动转盘,转出的数字大于3的概率是多少?(2)、现有两张分别写有3和4的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.①这三条线段能构成三角形的概率是.
②这三条线段能构成等腰三角形的概率是.
24. 如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,∠A=∠EDF=60°.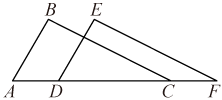 (1)、求证:△ABC≌△DEF;(2)、若∠B=100°,求∠F的度数.25. 李老师一直坚持步行上下班.一天,李老师下班后,从学校出发以45米/分的速度走了900米时,遇到一个朋友,停下来交流了半个小时,然后回家,如图所示是李老师从学校到家这一过程中,距离家的路程(米)与离开学校的时间(分)之间的关系.
(1)、求证:△ABC≌△DEF;(2)、若∠B=100°,求∠F的度数.25. 李老师一直坚持步行上下班.一天,李老师下班后,从学校出发以45米/分的速度走了900米时,遇到一个朋友,停下来交流了半个小时,然后回家,如图所示是李老师从学校到家这一过程中,距离家的路程(米)与离开学校的时间(分)之间的关系.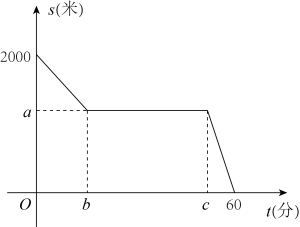 (1)、在如图所示反映的两个变量之间的关系中,自变量是;因变量是 .(2)、图中表示的数值是;表示的数值是;表示的数值是;(3)、李老师遇到朋友之前的行走速度快还是和朋友分开以后的行走速度快?和朋友分开后的平均速度是多少?26. “平方差公式”和“完全平方公式”应用非常广泛,灵活利用公式往往能化繁为简,巧妙解题.请阅读并解决下列问题:
(1)、在如图所示反映的两个变量之间的关系中,自变量是;因变量是 .(2)、图中表示的数值是;表示的数值是;表示的数值是;(3)、李老师遇到朋友之前的行走速度快还是和朋友分开以后的行走速度快?和朋友分开后的平均速度是多少?26. “平方差公式”和“完全平方公式”应用非常广泛,灵活利用公式往往能化繁为简,巧妙解题.请阅读并解决下列问题: (1)、问题一: ,
(1)、问题一: ,则 , ;
(2)、计算:;(3)、问题二:已知 ,则 , ;
(4)、已知长和宽分别为 , 的长方形,它的周长为14,面积为10,如图所示,求的值.27. (1)、模型的发现:
(1)、模型的发现:如图1,在中, , , 直线经过点 , 且、两点在直线的同侧,直线 , 直线 , 垂足分别为点 , . 请直接写出、和的数量关系.
(2)、模型的迁移1:位置的改变如图2,在(1)的条件下,若 , 两点在直线的异侧,请说明、和的关系,并证明.
(3)、模型的迁移2:角度的改变如图3,在(1)的条件下,若三个直角都变为了相等的钝角,即 , 其中 , (1)的结论还成立吗?若成立,请你给出证明;若不成立,请说明、和的关系,并证明.