山东省济南市商河县2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-08 类型:期末考试
一、单选题
-
1. 2022年冬奥会在北京举行,以下历届冬奥会会徽是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,将一副三角尺按下列位置摆放,使和互余的摆放方式是( )A、
2. 如图,将一副三角尺按下列位置摆放,使和互余的摆放方式是( )A、 B、
B、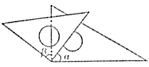 C、
C、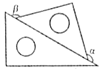 D、
D、 3. 有研究机构预测0.7纳米芯片将在2029年以后批量生产,“纳米”是长度单位,1纳米等于10米,0.7纳米用科学记数法表示为( )A、米 B、米 C、米 D、米4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,将直尺与角的三角尺叠放在一起,若 , 则的大小是( )
3. 有研究机构预测0.7纳米芯片将在2029年以后批量生产,“纳米”是长度单位,1纳米等于10米,0.7纳米用科学记数法表示为( )A、米 B、米 C、米 D、米4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,将直尺与角的三角尺叠放在一起,若 , 则的大小是( ) A、 B、 C、 D、6. 以下列数据为长度的三条线段,能组成三角形的是( )A、2cm、3cm、5cm B、2cm、3cm、4cm C、3cm、5cm、9cm D、8cm、4cm、4cm7. 小花放学回家走了一段路,在途径的书店买了一些课后阅读书籍,然后发现时间比较晚了,急忙跑步回到家.若设小花与家的距离为s(米),她离校的时间为t(分钟),则反映该情景的大致图象为( )A、
A、 B、 C、 D、6. 以下列数据为长度的三条线段,能组成三角形的是( )A、2cm、3cm、5cm B、2cm、3cm、4cm C、3cm、5cm、9cm D、8cm、4cm、4cm7. 小花放学回家走了一段路,在途径的书店买了一些课后阅读书籍,然后发现时间比较晚了,急忙跑步回到家.若设小花与家的距离为s(米),她离校的时间为t(分钟),则反映该情景的大致图象为( )A、 B、
B、 C、
C、 D、
D、 8. 不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是( )A、3个球都是黑球 B、3个球都是白球 C、三个球中有黑球 D、3个球中有白球9. 在△ABC中, , 则△ABC的形状是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、形状无法确定10. 如图,点E、F在BC上,BE=FC,∠B=∠C.添加下列条件无法证得△ABF≌△DCE的是( )
8. 不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是( )A、3个球都是黑球 B、3个球都是白球 C、三个球中有黑球 D、3个球中有白球9. 在△ABC中, , 则△ABC的形状是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、形状无法确定10. 如图,点E、F在BC上,BE=FC,∠B=∠C.添加下列条件无法证得△ABF≌△DCE的是( )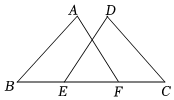 A、∠AFB=∠DEC B、AB=DC C、∠A=∠D D、AF=DE11. 如图,在△ABC中,DE是AC的垂直平分线,AC=6cm,且△ABD的周长为10cm,则△ABC的周长为( )
A、∠AFB=∠DEC B、AB=DC C、∠A=∠D D、AF=DE11. 如图,在△ABC中,DE是AC的垂直平分线,AC=6cm,且△ABD的周长为10cm,则△ABC的周长为( ) A、6cm B、10cm C、13cm D、16cm12. 如图,在与中, , , , , 交于点 , 连接下列结论:①;②;③;④ , 正确的个数为( )
A、6cm B、10cm C、13cm D、16cm12. 如图,在与中, , , , , 交于点 , 连接下列结论:①;②;③;④ , 正确的个数为( ) A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题
-
13. 如果一个角是70°,那么它的补角的度数为14. 在一个不透明的袋中装有个白色小球,个红色小球,小球除颜色外其他完全相同.若从中随机摸出一个球,恰为红球的概率为 , 则 .15. 如果 , 那么的值是 .16. 如图,的边长是10,边上的高是4,点D在上运动,设的长为x,请写出的面积y与x之间的关系式 .
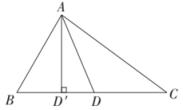 17. 如图中, , 以顶点为圆心,任意长为半径画弧,分别交、于点、 , 再分别以点、为圆心,大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是 .
17. 如图中, , 以顶点为圆心,任意长为半径画弧,分别交、于点、 , 再分别以点、为圆心,大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是 . 18. 如图,和是两个等腰直角三角形, , , , 的顶点在边上移动,在移动过程中,线段与线段相交于点 , 线段与线段相交于点 , 当为中点,连接、 , 若 , , , 则的长 .
18. 如图,和是两个等腰直角三角形, , , , 的顶点在边上移动,在移动过程中,线段与线段相交于点 , 线段与线段相交于点 , 当为中点,连接、 , 若 , , , 则的长 .
三、解答题
-
19. 计算:(1)、(2)、20. 先化简,再求值: , 其中 , .21. 向如图所示的正三角形区域内扔沙包,(区域中每个小正三角形陈颜色外完全相同)沙包随机落在某个正三角形内.
 (1)、扔沙包一次,落在图中阴影区域的概率是 .(2)、要使沙包落在图中阴影区域和空白区域的概率均为 , 还要涂黑几个小正三角形?请在图中画出.22. 如图,B,F,E,C在同一条直线上,∠A=∠D.
(1)、扔沙包一次,落在图中阴影区域的概率是 .(2)、要使沙包落在图中阴影区域和空白区域的概率均为 , 还要涂黑几个小正三角形?请在图中画出.22. 如图,B,F,E,C在同一条直线上,∠A=∠D. (1)、若∠A=78°,∠C=47°,求∠BFD的度数.(2)、若∠AEB+∠BFD=180°,求证:AB∥CD.23. 如图,和的顶点都在边长为的正方形网格的格点上,且和关于直线成轴对称.
(1)、若∠A=78°,∠C=47°,求∠BFD的度数.(2)、若∠AEB+∠BFD=180°,求证:AB∥CD.23. 如图,和的顶点都在边长为的正方形网格的格点上,且和关于直线成轴对称. (1)、直接写出的面积;(2)、请在如图所示的网格中作出对称轴直线;(3)、请在直线上作一点 , 使得最小.保留必要的作图痕迹24. 如图,在和中, , , , 连接 , , 当点 , , 在同一条直线上时,请判断线段和的数量及位置关系,并说明理由.
(1)、直接写出的面积;(2)、请在如图所示的网格中作出对称轴直线;(3)、请在直线上作一点 , 使得最小.保留必要的作图痕迹24. 如图,在和中, , , , 连接 , , 当点 , , 在同一条直线上时,请判断线段和的数量及位置关系,并说明理由. 25. 西工大启迪中学初一年级学生和老师一起到一条笔直的跑道上锻炼身体,学生到达起点后做了一会准备活动,老师先跑,当学生出发时,老师已经距起点200米了,他们距起点的距离s(米)与学生出发的时间t(秒)之间的关系如图所示(不完整),根据图中给出的信息,解答下列问题:
25. 西工大启迪中学初一年级学生和老师一起到一条笔直的跑道上锻炼身体,学生到达起点后做了一会准备活动,老师先跑,当学生出发时,老师已经距起点200米了,他们距起点的距离s(米)与学生出发的时间t(秒)之间的关系如图所示(不完整),根据图中给出的信息,解答下列问题: (1)、在上述变化过程中,自变量是 ,因变量是 ;(2)、老师和学生的速度分别为多少米/秒?(3)、学生与老师相遇 次,第二次相遇时距起点的距离为 米26. 在数学中,有许多关系都是在不经意间被发现的,请认真观察图形,解答下列问题:
(1)、在上述变化过程中,自变量是 ,因变量是 ;(2)、老师和学生的速度分别为多少米/秒?(3)、学生与老师相遇 次,第二次相遇时距起点的距离为 米26. 在数学中,有许多关系都是在不经意间被发现的,请认真观察图形,解答下列问题: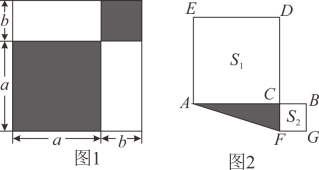 (1)、如图1,用两种不同的方法表示阴影图形的面积,得到一个等量关系: .(2)、若图1中a、b满足a+b=7,ab=10,求a2+b2的值;(3)、如图2,C是线段AB上一点,以AC,BC为边向两边作正方形,AC+BC=8,两正方形面积和S1+S2=40,求图中阴影部分面积.27. 数学模型学习与应用:
(1)、如图1,用两种不同的方法表示阴影图形的面积,得到一个等量关系: .(2)、若图1中a、b满足a+b=7,ab=10,求a2+b2的值;(3)、如图2,C是线段AB上一点,以AC,BC为边向两边作正方形,AC+BC=8,两正方形面积和S1+S2=40,求图中阴影部分面积.27. 数学模型学习与应用: (1)、【模型学习】:如图 , , , 于点 , 于点由 , 得;又 , 可以通过推理得到≌ , 进而得到 , 我们把这个数学模型称为“一线三等角”模型.(2)、【模型应用】:如图 , 为等边三角形, , , 求证:;(3)、【模型变式】:如图 , 在中, , , 于点 , 于点 , , , 则 .
(1)、【模型学习】:如图 , , , 于点 , 于点由 , 得;又 , 可以通过推理得到≌ , 进而得到 , 我们把这个数学模型称为“一线三等角”模型.(2)、【模型应用】:如图 , 为等边三角形, , , 求证:;(3)、【模型变式】:如图 , 在中, , , 于点 , 于点 , , , 则 .