山东省济南市平阴县2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-08 类型:期末考试
一、单选题
-
1. 下面是青岛、济南、郑州、太原四个城市的地铁图标,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 北斗系统是我国自主建设、独立运行的全球卫星导航系统,北斗系统的自主建设历程,也是一部技术创新引领、知识产权护航的发展史,在这些技术创新中,芯片技术的突破尤为关键.其中支持北斗三号新信号的纳米工艺射频基带一体化导航定位芯片,已实现规模化应用.纳米米,在这里将用科学记数法表示为( )A、 B、 C、 D、3. 在一个不透明袋子里装有红球、黄球共个,这些球除颜色外都相同,若从袋中任意取出一个球,取到红色球的概率为 , 则袋子中红球的个数最有可能是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列长度的三条线段,能组成三角形的是( )A、2cm,3cm,4cm B、2cm,3cm,5cm C、6cm,8cm,15cm D、2cm,5cm,8cm6. 如图,直线a,b相交于点O,如果 ,那么 是( )
2. 北斗系统是我国自主建设、独立运行的全球卫星导航系统,北斗系统的自主建设历程,也是一部技术创新引领、知识产权护航的发展史,在这些技术创新中,芯片技术的突破尤为关键.其中支持北斗三号新信号的纳米工艺射频基带一体化导航定位芯片,已实现规模化应用.纳米米,在这里将用科学记数法表示为( )A、 B、 C、 D、3. 在一个不透明袋子里装有红球、黄球共个,这些球除颜色外都相同,若从袋中任意取出一个球,取到红色球的概率为 , 则袋子中红球的个数最有可能是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列长度的三条线段,能组成三角形的是( )A、2cm,3cm,4cm B、2cm,3cm,5cm C、6cm,8cm,15cm D、2cm,5cm,8cm6. 如图,直线a,b相交于点O,如果 ,那么 是( )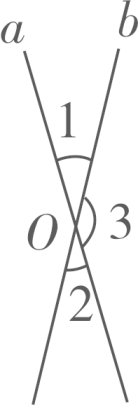 A、 B、 C、 D、7. 在下列各图的中,符合题意画出AC边上高的图形是( )A、
A、 B、 C、 D、7. 在下列各图的中,符合题意画出AC边上高的图形是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )
8. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )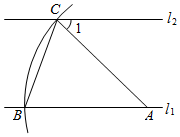 A、 B、 C、 D、9. 如图,在已知的中,按以下步骤作图:①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若 , , 则∠ACB的度数为( )
A、 B、 C、 D、9. 如图,在已知的中,按以下步骤作图:①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若 , , 则∠ACB的度数为( )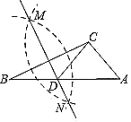 A、105° B、100° C、95° D、90°10. 如图,在△ABC中,AC=5,BC=12,AB=13,AD是角平分线,DE⊥AB,垂足为E,则△BDE的周长为( )
A、105° B、100° C、95° D、90°10. 如图,在△ABC中,AC=5,BC=12,AB=13,AD是角平分线,DE⊥AB,垂足为E,则△BDE的周长为( )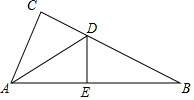 A、17 B、18 C、20 D、2511. 如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端米处,发现此时绳子底端距离打结处约米,则可算出旗杆的高度是米.( )
A、17 B、18 C、20 D、2511. 如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端米处,发现此时绳子底端距离打结处约米,则可算出旗杆的高度是米.( )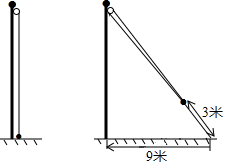 A、 B、 C、 D、12. 如图,在中, , 点为线段上一动点不与点 , 重合 , 连接 , 作 , 交线段于点下列结论:
A、 B、 C、 D、12. 如图,在中, , 点为线段上一动点不与点 , 重合 , 连接 , 作 , 交线段于点下列结论:;
若 , 则;
当时,则为中点;
当为等腰三角形时, .
其中正确的有个.( )
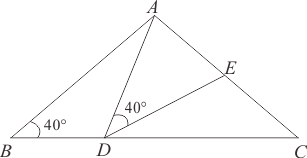 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. .14. 若(x+2)(x﹣4)=x2+nx﹣8,则n= .15. 如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是.
 16. 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的大小为度.
16. 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的大小为度.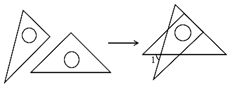 17. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为.
17. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为. 18. 如图 , , 点从出发,沿路线运动,到停止;点的速度为每秒 , 运动时间为秒,如图是的面积与秒的图象.根据题目中提供的信息,请你推断出 .
18. 如图 , , 点从出发,沿路线运动,到停止;点的速度为每秒 , 运动时间为秒,如图是的面积与秒的图象.根据题目中提供的信息,请你推断出 .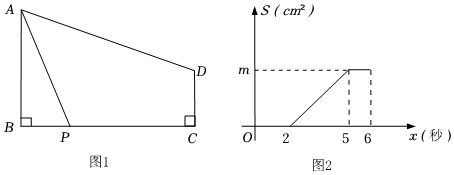
三、解答题
-
19. 计算:(1)、;(2)、 .20. 先化简,再求值: , 其中 .21. 请将下列证明过程补充完整:
如图,已知: , .
求证: .

证明:已知 ,
∴AB∥CD( )
▲ (两直线平行,同位角相等).
又已知 ,
▲ 等量代换 .
∴AD∥BE( )
( )
22. 如图, , 是线段上的两点, , EB∥CD, .求证: .
 23. 已如一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.(1)、求从中随机抽取出一个黑球的概率是多少?(2)、若往口袋中再放入2个白球,求从口袋中随机取出一个白球的概率是多少?24. 某剧院的观众席的座位为扇形,且按下列方式设置:
23. 已如一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.(1)、求从中随机抽取出一个黑球的概率是多少?(2)、若往口袋中再放入2个白球,求从口袋中随机取出一个白球的概率是多少?24. 某剧院的观众席的座位为扇形,且按下列方式设置:排数(x)
1
2
3
4
…
座位数(y)
50
53
56
59
…
(1)、按照上表所示的规律,当排数为6时,此时座位数为 .(2)、写出座位数y与排数x之间的关系式:;(3)、按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.25. 如图,方格纸中每个小方格都是边长为的正方形,四边形的顶点与点都是格点. (1)、作四边形关于直线对称的四边形 .(2)、求四边形的面积: .(3)、若在直线上有一点使得最小点位置如图所示 , 连接 , 请求出此时的 ▲ .26. “低碳环保、绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车沿同一路线去图书馆,爸爸先以米分的速度骑行一段时间,休息了分钟,再以米分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程米与时间分钟的关系如图.请结合图象,解答下列问题:
(1)、作四边形关于直线对称的四边形 .(2)、求四边形的面积: .(3)、若在直线上有一点使得最小点位置如图所示 , 连接 , 请求出此时的 ▲ .26. “低碳环保、绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车沿同一路线去图书馆,爸爸先以米分的速度骑行一段时间,休息了分钟,再以米分的速度到达图书馆.小军始终以同一速度骑行,两人行驶的路程米与时间分钟的关系如图.请结合图象,解答下列问题: (1)、a=;b= .(2)、求出的取值是多少?(3)、若小军的速度是米分,求小军在图中与爸爸第二次相遇时的时间.27. 如图,和都是等边三角形.
(1)、a=;b= .(2)、求出的取值是多少?(3)、若小军的速度是米分,求小军在图中与爸爸第二次相遇时的时间.27. 如图,和都是等边三角形. (1)、如图 , 线段与是否相等?若相等,加以证明;若不相等,请说明理由.(2)、如图 , 若、、三点在一条直线上,与交于点 , 求的度数.(3)、如图 , 若、、三点不在一条直线上, , , , 求的长.
(1)、如图 , 线段与是否相等?若相等,加以证明;若不相等,请说明理由.(2)、如图 , 若、、三点在一条直线上,与交于点 , 求的度数.(3)、如图 , 若、、三点不在一条直线上, , , , 求的长.