山东省济南市历下区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-08 类型:期末考试
一、单选题
-
1. 自新冠肺炎疫情发生以来,全国人民共同抗疫,全面普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 小明有两根长度为5cm,10cm的木棒,他想钉一个三角形木框,桌上有几根木棒供他选择,他有几种选择?( )
2. 小明有两根长度为5cm,10cm的木棒,他想钉一个三角形木框,桌上有几根木棒供他选择,他有几种选择?( ) A、1种 B、2种 C、3种 D、4种3. 如图所示,若AB∥CD, , 则( )
A、1种 B、2种 C、3种 D、4种3. 如图所示,若AB∥CD, , 则( ) A、 B、 C、 D、4. “梦想从学习开始,事业从实践起步”,近来,每天登录“学习强国”APP,学精神、增能量、看文化长见识已经成为一种学习新风尚.下面是小颖爸爸上周“学习强国”周积分与学习天数的有关数据,则下列说法错误的是( )
A、 B、 C、 D、4. “梦想从学习开始,事业从实践起步”,近来,每天登录“学习强国”APP,学精神、增能量、看文化长见识已经成为一种学习新风尚.下面是小颖爸爸上周“学习强国”周积分与学习天数的有关数据,则下列说法错误的是( )
学习天数n(天)
1
2
3
4
5
6
7
周积分w(分)
55
110
165
220
275
330
385
A、在这个变化过程中,学习天数是自变量,周积分是因变量 B、周积分随学习天数的增加而增加 C、周积分w与学习天数n的关系式为 D、天数每增加1天,周积分的增长量不一定相同5. 下列运算正确的是( )A、 B、 C、 D、6. 下列说法正确的是( )A、小丽买一张体育彩票中“一等奖”是随机事件 B、任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件 C、“清明时节雨纷纷”是必然事件 D、若a是有理数,则“”是不可能事件7. 如图,把两根钢条AB,CD的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳)只要量得AC的长度,就可知工件的内径BD是否符合标准,这是利用的什么数学原理呢?( )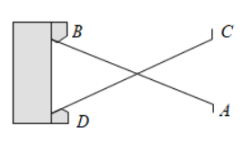 A、SSS B、SAS C、ASA D、AAS8. 一个质量均匀的正方体骰子,六个面分别标有1,2,3,4,5,6,任意掷一次骰子,掷出结果为“2的倍数”的概率为( )A、 B、 C、 D、9. 一个袋中装有3个红球,2个白球和4个黄球,每个球除颜色外均相同.从袋中任意摸出一个球,取到黄色球的概率为( )A、 B、 C、 D、10. 如图所示,将一张长方形纸片斜折过去,使顶点A落在处,BC为折痕,然后再把BE折过去,使之与重合,折痕为BD,若 , 则的度数为( )
A、SSS B、SAS C、ASA D、AAS8. 一个质量均匀的正方体骰子,六个面分别标有1,2,3,4,5,6,任意掷一次骰子,掷出结果为“2的倍数”的概率为( )A、 B、 C、 D、9. 一个袋中装有3个红球,2个白球和4个黄球,每个球除颜色外均相同.从袋中任意摸出一个球,取到黄色球的概率为( )A、 B、 C、 D、10. 如图所示,将一张长方形纸片斜折过去,使顶点A落在处,BC为折痕,然后再把BE折过去,使之与重合,折痕为BD,若 , 则的度数为( ) A、 B、 C、 D、11. 小颖给同学们讲了一个她自己编的“龟兔赛跑”的故事,小聪根据小颖讲的故事画出了如图所示的图象,表示了龟和兔已走路程S(米)和所用时间t(分钟)的关系图,小华根据小聪画的图象得出了以下结论:
A、 B、 C、 D、11. 小颖给同学们讲了一个她自己编的“龟兔赛跑”的故事,小聪根据小颖讲的故事画出了如图所示的图象,表示了龟和兔已走路程S(米)和所用时间t(分钟)的关系图,小华根据小聪画的图象得出了以下结论:⑴描述的是乌龟的行进情况,描述的是兔子的行进情况;
⑵乌龟和兔子是从同一地点出发的;
⑶乌龟和兔子在比赛途中相遇了两次;
⑷在时刻,兔子在乌龟的前面,结论正确的有( )个
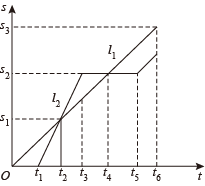 A、4 B、3 C、2 D、112. 如图,将沿AC所在的直线翻折得到 , 再将沿所在的直线翻折得到 , 点在同一条直线上, , 则( )
A、4 B、3 C、2 D、112. 如图,将沿AC所在的直线翻折得到 , 再将沿所在的直线翻折得到 , 点在同一条直线上, , 则( )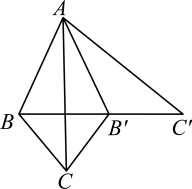 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 化简: .14. 计算: .15. 如图是一个寻宝游戏的戴宝图,分别有“花朵”,“太阳”,“月亮”三种图案,宝物(只有一个)藏在“月亮”下的概率是 .
 16. 如图,AB是线段CD的垂直平分线,E是AB上一点,若 , 则°.
16. 如图,AB是线段CD的垂直平分线,E是AB上一点,若 , 则°.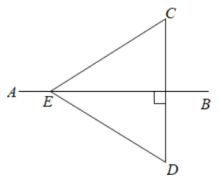 17. 如图,梯形的上底是x,高是8,下底是15,面积是y,当x增加4时,y增加 .
17. 如图,梯形的上底是x,高是8,下底是15,面积是y,当x增加4时,y增加 .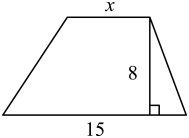 18. 如图,和都是等边三角形,连接HG,EI交于点P,则度.
18. 如图,和都是等边三角形,连接HG,EI交于点P,则度.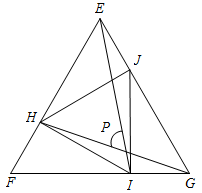
三、解答题
-
19. 计算:(1)、;(2)、 .20. 解答:
 (1)、如图,在方格纸中,画出关于直线MN对称的图形;(2)、在对称轴MN上求一点P,使得最短.21. 先化简,再求值: , 其中 .22. 已知:在如图所示的“风筝”图案中,AB=AD,∠C=∠E,∠BAE=∠DAC.求证:AC=AE.
(1)、如图,在方格纸中,画出关于直线MN对称的图形;(2)、在对称轴MN上求一点P,使得最短.21. 先化简,再求值: , 其中 .22. 已知:在如图所示的“风筝”图案中,AB=AD,∠C=∠E,∠BAE=∠DAC.求证:AC=AE. 23. 小蒙设计了两个抽奖游戏,游戏一是转盘游戏,如图,转盘被等分成了4个扇形,共有红、黄和蓝三种颜色,自由转动转盘,指针停在红色时会得到奖励;游戏二是摸球游戏,袋子里有2个红球、2个黄球和1个蓝球,每个球除颜色外都相同,任意摸出一个球,摸到红球会得到奖励.小雨要参加抽奖游戏,你建议她参加哪一个游戏?请说明理由.
23. 小蒙设计了两个抽奖游戏,游戏一是转盘游戏,如图,转盘被等分成了4个扇形,共有红、黄和蓝三种颜色,自由转动转盘,指针停在红色时会得到奖励;游戏二是摸球游戏,袋子里有2个红球、2个黄球和1个蓝球,每个球除颜色外都相同,任意摸出一个球,摸到红球会得到奖励.小雨要参加抽奖游戏,你建议她参加哪一个游戏?请说明理由. 24. 如图,小长方形的长为a,宽为b,将七个这样的小长方形放在大长方形ABCD中,大长方形中未被覆盖的两个部分的面积分别记为和 .
24. 如图,小长方形的长为a,宽为b,将七个这样的小长方形放在大长方形ABCD中,大长方形中未被覆盖的两个部分的面积分别记为和 . (1)、若 , 求的值(用含有a,b的字母表示);(2)、若的值为ab,求a与b的数量关系.25. 在中,BD和CE分别是和的角平分线,BD,CE相交于点O.
(1)、若 , 求的值(用含有a,b的字母表示);(2)、若的值为ab,求a与b的数量关系.25. 在中,BD和CE分别是和的角平分线,BD,CE相交于点O. (1)、如图1,若 , , 求的度数;(2)、借助图1,若 , , 求与的关系;(3)、如图2,若 , 求证: .26. 小明从学校步行去美术馆,同时小红骑车从美术馆回学校,两人都沿同一条路直线运动,小红回到学校停留三分钟后又以同样的速度去美术馆,小明的速度是80米/分钟,如图是两人与学校的距离s(米)与小明的运动时间t(分钟)之间的关系图.
(1)、如图1,若 , , 求的度数;(2)、借助图1,若 , , 求与的关系;(3)、如图2,若 , 求证: .26. 小明从学校步行去美术馆,同时小红骑车从美术馆回学校,两人都沿同一条路直线运动,小红回到学校停留三分钟后又以同样的速度去美术馆,小明的速度是80米/分钟,如图是两人与学校的距离s(米)与小明的运动时间t(分钟)之间的关系图.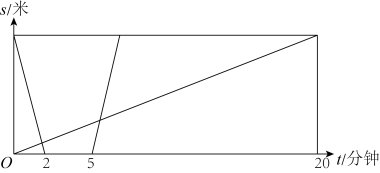 (1)、学校与美术馆之间的距离为米;(2)、求小红停留再出发后s与t的关系式;(3)、请直接写出小明和小红在途中相遇时小明的运动时间.27. 在直角三角形中,三边存在特殊的关系:两直角边的平方和等于斜边的平方,如图1,因为 , 所以 . 这种特殊的关系被称为勾股定理.
(1)、学校与美术馆之间的距离为米;(2)、求小红停留再出发后s与t的关系式;(3)、请直接写出小明和小红在途中相遇时小明的运动时间.27. 在直角三角形中,三边存在特殊的关系:两直角边的平方和等于斜边的平方,如图1,因为 , 所以 . 这种特殊的关系被称为勾股定理.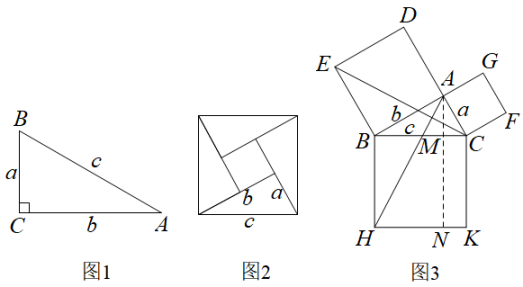
勾股定理的证明方法非常丰富,达数百种之多,其中比较出名的,有东汉数学家赵爽的“勾股圆方图”(见《周髀算经》)和政几里得的证法(见《几何原本》).
(1)、赵爽的证明方法:如图2,四个全等的直角三角形拼成了一个大正方形,中间空白的部分是小正方形,设直角三角形的两条直角边分别为a和b,斜边为c,则小正方形的边长为;在此基础上,大正方形的面积可以直接表示为 , 还可以表示为四个直角三角形与小正方形的面积之和,为 . 于是得到等式;化简后可得 .(2)、欧几里得的证明方法:①如图3,设的两条直角边分别为a和b,斜边为c,分别以这三条边为边,向外做三个正方形,得到正方形ADEB,正方形ACFG和正方形BHKC,连接EC与AH,做交HK于N,交BC于M,首先请证明
②
正方形ADEB与同底等高,长方形BHNM与同底等高,
= ,
,
同理可得
所以:
即 .