山东省济南市历城区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-09-08 类型：期末考试

进入出卷网下载

一、单选题

1. 2022年2月4日至2月20日，第24届冬奥会在中国北京市和张家口市联合举办．下列冬奥元素中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 全球可被人类利用的淡水总量约占地球上总水量的0.00003，因此珍惜水，保护水是每个公民的责任．其中数字0.00003用科学记数法表示为（）

A、3×10^-5 B、3×10^-4 C、0.3×10^-5 D、0.3×10^-4

查看试题解析
3. 下列事件中，是随机事件的是（）

A、任意画一个三角形，其内角和是180° B、经过有交通信号灯的路口，刚好是红灯 C、投一枚骰子，朝上一面的点数是7 D、从只装有红球和黄球的袋中，掏出一个球是黑球

查看试题解析
4. 下列计算正确的是（）

A、a⁶÷a²＝a³ B、a⁶·a²＝a¹² C、（－2a²）²＝4a⁴ D、b³＋b²＝2b⁵

查看试题解析
5. 如图，将一块含有30°的直角三角板的顶点放在直尺的一边上，若∠1＝46°，那么∠2的度数是（）

A、114° B、124° C、94° D、104°

查看试题解析
6. 一个均匀的小球在如图所示的水平地板上自由滚动，并随机停在某块方砖上，若每一块方砖除颜色外完全相同，那么小球最终停留在黑砖上的概率是（）

A、 $\frac{4}{9}$ B、 $\frac{5}{9}$ C、 $\frac{4}{5}$ D、1

查看试题解析
7. 若一个等腰三角形的周长是10，其中一边长为2，则这个等腰三角形底边的长度为（）

A、2或6 B、6 C、2或8 D、2

查看试题解析
8. 如图，y＝2x＋10表示了自变量x与因变量y的关系，当x每增加1时，y增加（）

A、1 B、2 C、6 D、12

查看试题解析
9. 6月12日，京张高铁轨道全线贯通，它是2022年北京冬奥会的重要交通保障设施.全线运营后高铁将通过清华园隧道穿越北京市城市核心区，如图所示，当高铁匀速通过清华园隧道（隧道长大于火车长）时，高铁在隧道内的长度 $y$ 与高铁进入隧道的时间 $x$ 之间的关系用图象描述大致是（）

A、 B、 C、 D、

查看试题解析
10. 如图，按以下方法作一个角的平分线：（1）以O为圆心，适当长为半径画弧，分别交OA、OB于点M、N．（2）分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧在∠AOB的内部相交于点C．（3）画射线OC，射线OC即为所求．这种作图方法的依据是（）

A、AAS B、SAS C、SSS D、ASA

查看试题解析
11. 如图，在△ABC中，AB、AC的垂直平分线分别交BC于点E、F，若∠BAC＝114°，则∠EAF为（）

A、40° B、44° C、48° D、52°

查看试题解析
12. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ，以 $A C$ 为边，作 $△ A C D$ ，满足 $A D = A C$ ， $E$ 为 $B C$ 上一点，连接 $A E$ ， $∠ C A D = 2 ∠ B A E$ ，连接 $D E$ ，下列结论中：① $∠ A D E = ∠ A C B$ ；② $A C ⊥ D E$ ；③ $∠ A E B = ∠ A E D$ ；④ $D E = C E + 2 B E$ ．其中正确的有（）

A、①②③ B、③④ C、①④ D、①③④

查看试题解析

二、填空题

13. 若点 $P (m - 2 ， 3)$ 在 $y$ 轴上，则m的值为．

查看试题解析
14. 已知三角形的两边长分别为 $2$ 和 $4$ ，第三边长为 $x$ ，若 $x$ 为整数，请写出一个适合的x值为．

查看试题解析
15. 等腰三角形一内角为40°，则该等腰三角形顶角的度数为．

查看试题解析
16. 如表反映的是高速路上匀速行驶的汽车在行驶过程中时x（时）与邮箱的余油量y （升）之间的关系，写出y与x的函数表达式
行驶时间x（时）
0
1
2
3
…
余油量y（升）
60
50
40
30
…

查看试题解析
17. 如图，折叠直角三角形纸片 $A B C$ ，使得点 $A$ 与点 $C$ 重合，折痕为 $D E$ ．若 $A B = 4$ ， $B C = 3$ ，则 $C D$ 的长是．

查看试题解析
18. 如图，在Rt△ABC中，∠C＝90°，AC＝4，AB＝5．点E为边AC上的动点，点F为边AB上的动点，则线段FE＋EB的最小值是．

查看试题解析

三、解答题

19. 填写推理理由
如图：EF∥AD，∠1＝∠2，∠BAC＝70°，把求∠AGD的过程填写完整．
证明：∵EF∥AD
∴∠2＝  ▲  （       ）
又∵∠1＝∠2
∴∠1＝∠3  ▲
∴AB∥  ▲  （            ）
∴∠BAC＋  ▲  ＝180°（           ）
又∵∠BAC＝70°
∴∠AGD＝  ▲

查看试题解析
20. 计算：

(1)、 $(- 1)^{2022} \times (π - 2)^{0} + | - 5 | + (\frac{1}{2})^{- 2}$ ；

(2)、 $(- \frac{1}{3} a^{2} b)^{2} \cdot 9 a b^{3} \div a^{4} b^{3}$ ；

(3)、 $(\frac{2}{3} m^{2} n - 6 m n) \cdot \frac{3}{2} m n^{2}$ ；

(4)、 $(x + y + 1) (x + y - 1)$ ．

查看试题解析
21. 先化简，再求值： $[(x + y) (x - y) - (x - y)^{2}] \div 2 y$ ，其中 $x = 2022$ ， $y = 1$ ．

查看试题解析
22. 如图， $A B ∥ C D$ ， $A B = C D$ ， $C E = B F$ ．判断 $D F$ 与 $A E$ 的数量关系，并说明你的理由．

查看试题解析
23. 如图，在正方形网格上有一个△ABC，三个顶点都在格点上，网格上的最小正方形的边长为1．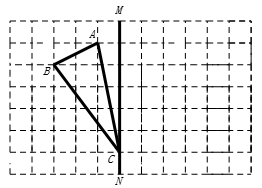

(1)、作△ABC关于直线MN的对称图形△A′B′C′（不写作法）；

(2)、求BC的长；

(3)、求△ABC的面积．

查看试题解析
24. 在一个口袋中只装有4个白球和6个红球，它们除颜色外完全相同.

(1)、事件“从口袋中随机摸出一个球是绿球”发生的概率是；

(2)、事件“从口袋中随机摸出一个球是红球”发生的概率是；

(3)、现从口袋中取走若干个红球，并放入相同数量的白球，充分摇匀后，要使从口袋中随机摸出一个球是白球的概率是 $\frac{4}{5}$ ，求取走了多少个红球？

查看试题解析
25. 已知动点 $P$ 以 $2 c m / s$ 的速度沿如图1所示的边框以 $B - C - D - E - F - A$ 的路径运动，记 $△ A B P$ 的面积为 $s (c m^{2})$ ， $s$ 与运动时间 $t (s)$ 的关系如图2所示，若 $A B = 6 c m$ ．
请回答下列问题：

(1)、图1中 $B C =$ $c m$ ， $C D =$ $c m$ ． $D E =$ $c m$ ．

(2)、求图2中 $m$ ， $n$ 的值；

(3)、分别求出当点 $P$ 在线段 $B C$ 和 $D E$ 上运动时 $s$ 与 $t$ 的关系式．

查看试题解析
26.

(1)、方法呈现：

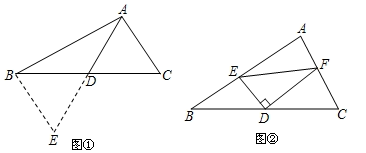
如图①：在 $△ A B C$ 中，若 $A B = 6$ ， $A C = 4$ ，点D为BC边的中点，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使 $D E = A D$ ，再连接BE，可证 $△ A C D ≌ △ E B D$ ，从而把AB、AC， $2 A D$ 集中在 $△ A B E$ 中，利用三角形三边的关系即可判断中线AD的取值范围是，这种解决问题的方法我们称为倍长中线法；

(2)、探究应用：
如图②，在 $△ A B C$ 中，点D是BC的中点， $D E ⊥ D F$ 于点D，DE交AB于点E，DF交AC于点F，连接EF，判断 $B E + C F$ 与EF的大小关系并证明；

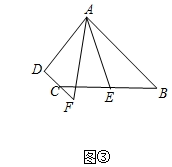
(3)、问题拓展：
如图③，在四边形ABCD中， $A B / / C D$ ， AF与DC的延长线交于点F、点E是BC的中点，若AE是 $∠ B A F$ 的角平分线．试探究线段AB，AF，CF之间的数量关系，并加以证明．

查看试题解析

行驶时间x（时）	0	1	2	3	…
余油量y（升）	60	50	40	30	…