山东省德州市夏津县2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-08 类型:期末考试
一、单选题
-
1. 某中学为了了解学校520名学生的睡眠情况,抽查了其中100名学生的睡眠时间进行统计,下列叙述正确的是( )A、以上调查属于全面调查 B、100名学生是总体的一个样本 C、520是样本容量 D、每名学生的睡眠时间是一个个体2. 在平面直角坐标系中,若点P(m,1)在第二象限内,则m的取值可以是( )A、1 B、-3 C、4 D、4或-43. 如图,点在直线上, . 若 , 则的大小为( )
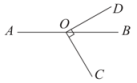 A、120° B、130° C、140° D、150°4. 若代数式的值是非负数,则的取值范围是( )A、 B、 C、 D、5. 下列说法中错误的是( )A、是整数 B、是有理数 C、是分数 D、的立方根是无理数6. 岛P位于岛Q的正西方,由岛P、Q分别测得船R位于南偏东30°和南偏西45°方向上.符合条件的示意图是( )A、
A、120° B、130° C、140° D、150°4. 若代数式的值是非负数,则的取值范围是( )A、 B、 C、 D、5. 下列说法中错误的是( )A、是整数 B、是有理数 C、是分数 D、的立方根是无理数6. 岛P位于岛Q的正西方,由岛P、Q分别测得船R位于南偏东30°和南偏西45°方向上.符合条件的示意图是( )A、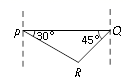 B、
B、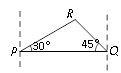 C、
C、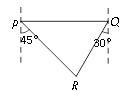 D、
D、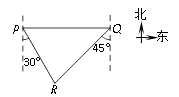 7. 一个等腰三角形的两边长分别为6和12,则这个等腰三角形的周长为( )A、30 B、24 C、18 D、24或308. 某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应该如何分配工人才能使生产的螺栓和螺帽刚好配套?若设生产螺栓x人,生产螺帽y人,则列方程组得( )A、 B、 C、 D、9. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、过C作EF AB
7. 一个等腰三角形的两边长分别为6和12,则这个等腰三角形的周长为( )A、30 B、24 C、18 D、24或308. 某车间有90名工人,每人每天平均能生产螺栓15个或螺帽24个,要使一个螺栓配套两个螺帽,应该如何分配工人才能使生产的螺栓和螺帽刚好配套?若设生产螺栓x人,生产螺帽y人,则列方程组得( )A、 B、 C、 D、9. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、过C作EF AB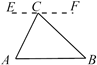 B、过AB上一点D作DE BC,DF AC
B、过AB上一点D作DE BC,DF AC 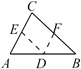 C、延长AC到F,过C作CE AB
C、延长AC到F,过C作CE AB  D、作CD⊥AB于点D
D、作CD⊥AB于点D 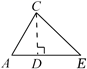 10. 如图,在△ABC中,AC=8,∠A=45°,∠B=105°,把△ABC沿水平向右方向平移到△DEF的位置,若CF=3,则下列结论中错误的是( )
10. 如图,在△ABC中,AC=8,∠A=45°,∠B=105°,把△ABC沿水平向右方向平移到△DEF的位置,若CF=3,则下列结论中错误的是( )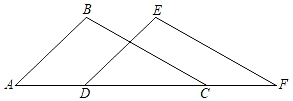 A、AD=3 B、∠F=30° C、AB∥DE D、DC=411. 下列四个命题:①对顶角相等;②点到直线的垂线段叫做点到直线的距离;③如果 , , 那么;④三角形的一个外角大于任何一个内角;⑤过一点有且只有一条直线与已知直线平行.其中真命题有( )A、4个 B、3个 C、2个 D、1个12. 一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )
A、AD=3 B、∠F=30° C、AB∥DE D、DC=411. 下列四个命题:①对顶角相等;②点到直线的垂线段叫做点到直线的距离;③如果 , , 那么;④三角形的一个外角大于任何一个内角;⑤过一点有且只有一条直线与已知直线平行.其中真命题有( )A、4个 B、3个 C、2个 D、1个12. 一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( ) A、(4,O) B、(5,0) C、(0,5) D、(5,5)
A、(4,O) B、(5,0) C、(0,5) D、(5,5)二、填空题
-
13. 9的算术平方根是 .14.
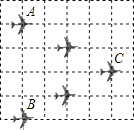
如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是 .
 15. 如图,△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积.
15. 如图,△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积.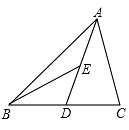 16. 点P(x,y)在第四象限,且 , 点P到y轴的距离是3,则P点坐标为 .17. 如图,则∠A+∠B+∠C+∠D+∠E的度数是.
16. 点P(x,y)在第四象限,且 , 点P到y轴的距离是3,则P点坐标为 .17. 如图,则∠A+∠B+∠C+∠D+∠E的度数是.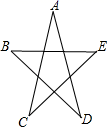 18. 若关于x、y的二元一次方程组 ,的解是 ,则关于a、b的二元一次方程组 的解是 .
18. 若关于x、y的二元一次方程组 ,的解是 ,则关于a、b的二元一次方程组 的解是 .三、解答题
-
19.(1)、计算:(2)、解方程组:20. 题目:≥
学生:老师,小聪把这道题后面的部分擦掉了.
老师:哦,如果我告诉你这道题的符合题意答案是x≥7,且后面 □ 是一个常数项,你能把这个常数项补上吗?
学生:我知道了.
根据以上的信息,请你求出□ 中的数.
21. 某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班50名学生的处理方式进行统计,得出相关统计表和统计图,请根据统计表图所提供的信息回答下列问题: (1)、统计表中的m= , n=;(2)、补全频数分布直方图;(3)、若该校共有2000名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?22. 如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)、统计表中的m= , n=;(2)、补全频数分布直方图;(3)、若该校共有2000名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?22. 如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.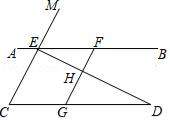 (1)、求证:CE∥GF;(2)、试判断∠AED与∠D之间的数量关系,并说明理由;(3)、若∠EHF=80°,∠D=30°,求∠AEM的度数.23. 小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,
(1)、求证:CE∥GF;(2)、试判断∠AED与∠D之间的数量关系,并说明理由;(3)、若∠EHF=80°,∠D=30°,求∠AEM的度数.23. 小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,商品名
单价(元)
数量(个)
金额(元)
签字笔
3
2
6
自动笔
1.5

记号笔
4

软皮笔记本

2
9
圆规
3.5
1

合计
8
28
解决下列问题:
(1)、小丽买了自动笔、记号笔各几支?(2)、小丽打算购买签字笔和自动笔共10只,购买签字笔的数量不少于自动笔数量的 , 且总费用不超过25元.问小丽共有几种购买方案,哪一种方案花费最少,最少花费为多少元?24. 阅读材料:对x,y定义一种新运算“T”,规定: (其中a,b均为非0常数,且).如 , 若 , .(1)、求a,b的值;(2)、求T(4,3)的值;(3)、若关于c的不等式组恰好有3个整数解,求实数m的取值范围.25. 如图,在平面直角坐标系中,点A、B是x轴、y轴上的点,若3是的立方根,也是的算术平方根,且 , , 将点B向左平移18个单位长度得到点C.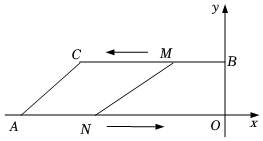 (1)、求点A、B、C的坐标;(2)、点M、N分别为线段BC、OA上的两个动点,点M从点B以1个单位长度/秒的速度向左运动,同时点N从点A以2个单位长度/秒的速度向右运动,设运动时间为t秒().
(1)、求点A、B、C的坐标;(2)、点M、N分别为线段BC、OA上的两个动点,点M从点B以1个单位长度/秒的速度向左运动,同时点N从点A以2个单位长度/秒的速度向右运动,设运动时间为t秒().①当时时,求t的值;
②是否存在一段时间,使得?若存在,求出t的取值范围;若不存在,请说明理由.