山东省德州市平原县2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-09-08 类型：期末考试

进入出卷网下载

一、单选题

1. 9的算术平方根是（）

A、3 B、-3 C、±3 D、81

查看试题解析
2. 下列不等式变形中错误的是（）

A、由 $a > b$ ，得 $a - 1 > b - 1$ B、由 $- \frac{1}{2} a < b$ ，得 $a > - 2 b$ C、由 $\frac{1}{2} a > \frac{1}{3} b$ ，得 $3 a > 2 b$ D、由 $- 3 a > 1$ ，得 $a > - \frac{1}{3}$

查看试题解析
3. 以下问题不适合用全面调查的是（）

A、了解我县某中学初一（6）班学生每周体育锻炼的时间 B、疫情中高风险区回我县人员的核算检测 C、了解我县中小学生每天的零花钱 D、我县某学校招聘老师对应聘老师的面试

查看试题解析
4. 在实数 $\sqrt{8}$ ， $- \sqrt{5}$ ， $\frac{π}{2}$ ， $\sqrt[3]{8}$ ， 3.14， $\sqrt{4}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，AB∥DF，AC⊥CE于C，BC与DF交于点E，若∠A=22°，则∠CEF等于（）

A、 $112 °$ B、 $102 °$ C、 $78 °$ D、 $68 °$

查看试题解析
6. 在同一平面内，a，b，c是直线，下列说法正确的是（）

A、若a∥b，b∥c，则a∥c B、若a⊥b，b⊥c，则a⊥c C、若a∥b，b⊥c，则a∥c D、若a∥b，b∥c，则a⊥c

查看试题解析
7. 已知 $A$ 的坐标为 $(1, 2)$ ，直线 $A B / / x$ 轴，且 $A B = 5$ ，则点 $B$ 的坐标为（）

A、 $(1, 7)$ B、 $(1, 7)$ 或 $(1, - 3)$ C、 $(6, 2)$ D、 $(6, 2)$ 或 $(- 4, 2)$

查看试题解析
8. 如果 $a < b < 0$ ，下列不等式中错误的是（）

A、 $a b > 0$ B、 $\frac{a}{b} < 1$ C、 $a + b < 0$ D、 $a - b < 0$

查看试题解析
9. 下列语句正确的是（）

A、在平面直角坐标系中， $(- 3, 5)$ 与 $(5, - 3)$ 表示两个不同的点 B、平行于 $x$ 轴的直线上所有点的横坐标都相同、 C、若点 $P (a, b)$ 在 $y$ 轴上，则 $b = 0$ D、点 $P (- 3, 4)$ 到 $x$ 轴的距离为3

查看试题解析
10. 已知：如图 $AB / / EF$ ， $BC ⊥ CD$ ，则 $∠ α$ ， $∠ β$ ， $∠ γ$ 之间的关系是 $($ $)$

A、 $∠ β = ∠ α + ∠ γ$ B、 $∠ α + ∠ β + ∠ γ = 180^{\circ}$ C、 $∠ α + ∠ β - ∠ γ = 90^{\circ}$ D、 $∠ β + ∠ γ - ∠ α = 90^{\circ}$

查看试题解析
11. 在解方程组 ${\begin{array}{l} ● x - 2 y = 5 \\ 7 x - 4 y = ★ \end{array}$ 时，小明由于粗心把系数 $●$ 抄错了，得到的解是 ${\begin{array}{l} x = - \frac{1}{3} \\ y = - \frac{10}{3} \end{array}$ ．小亮把常数 $★$ 抄错了，得到的解是 ${\begin{array}{l} x = - 9 \\ y = - 16 \end{array}$ ，则原方程组的符合题意解是（）

A、 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = - 1 \\ y = 1 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$

查看试题解析
12. 在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．如图，由里向外数第2个正方形开始，分别是由第1个正方形各顶点的横坐标和纵坐标都乘2，3，…得到的，请你观察图形，猜想由里向外第2022个正方形四条边上的整点个数共有（）

A、2022个 B、4044个 C、6066个 D、8088个

查看试题解析

二、填空题

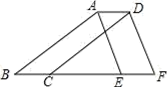
13. 如果 $a - 3 b = - 3$ ，那么代数式 $5 - a + 3 b$ 的值是．

查看试题解析
14. 若关于x、y的二元一次方程组 ${\begin{array}{l} x + y = 5 k \\ x - y = 9 k \end{array}$ 的解也是二元一次方程 $x - 2 y = 22$ 的解，则k的值为.

查看试题解析
15. 如图，将三角形ABE向右平移1cm得到三角形DCF，如果三角形ABE的周长是10cm，那么四边形ABFD的周长是．

查看试题解析
16. 若不等式组 ${\begin{array}{l} x - a > 2 \\ b - 2 x > 0 \end{array}$ 的解集为 $- 1 < x < 1$ ，则a+b的立方根是．

查看试题解析
17. 如图，将一等边三角形的三条边各8等分，按顺时针方向（图中箭头方向）标注各等分点的序号0、1、2、3、4、5、6、7、8，将不同边上的序号和为8的两点依次连接起来，这样就建立了“三角形”坐标系.在建立的“三角形”坐标系内，每一点的坐标用过这一点且平行（或重合）于原三角形三条边的直线与三边交点的序号来表示（水平方向开始、按顺时针方向、取与三角形外箭头方向一致的一侧序号），如点A的坐标可表示为 $(1 ， 2 ， 5)$ ，点B的坐标可表示为 $(4 ， 3 ， 1)$ ，按此方法，若点C的坐标为 $(3 ， m ， m - 1)$ ，则m＝.

查看试题解析

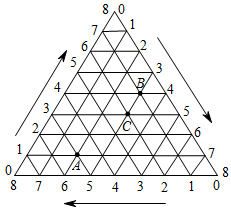
三、解答题

18.

(1)、解方程组： ${\begin{array}{l} 4 x + 3 y = 6 \\ 2 x - y = 8 \end{array}$ ；

(2)、解不等式组： ${\begin{array}{l} 4 x - 3 \geq x - 6 \\ x - 3 > \frac{4 x - 7}{2} \end{array}$ ．

查看试题解析
19. 如图，在正方形网格中，若点A的坐标是(1，2)，点B的坐标是(2，1)．

(1)、依题意，在图中建立平面直角坐标系；

(2)、图中点C的坐标是，

(3)、若点D的坐标为(0，3)，在图中标出点D的位置；

(4)、将点B向左平移3个单位长度，再向上平移1个单位长度，则所得的点 $B^{'}$ 的坐标是， △ $A B^{'} C$ 的面积为．

查看试题解析
20. 针对春节期间新型冠状病毒事件，九（1）班学生参加学校举行的“珍惜生命．远离病毒”知识竞赛初赛，赛后班长对成绩进行分析，制作如下的频数分布表、频数分布直方图和扇形统计图（未完成）．
类别
分数段
频数（人数）
A
60≤x＜70
a
B
70≤x＜80
16
C
80≤x＜90
24
D
90≤x＜100
6
请根据以上统计图表解答下列问题：

(1)、该班总人数为；

(2)、频数分布表中a=；

(3)、扇形统计图中，类别B所在扇形的圆心角是．

(4)、全校共有720名学生参加初赛，估计该校成绩“D”（90≤x<100范围内）的学生有多少人?

查看试题解析
21. “震灾无情人有情”．民政局将全市为四川受灾地区捐赠的物资打包成件，其中帐篷和食品共320件，帐篷比食品多80件．

(1)、求打包成件的帐篷和食品各多少件？

(2)、现计划租用甲、乙两种货车共8辆，一次性将这批帐篷和食品全部运往受灾地区．已知甲种货车最多可装帐篷40件和食品10件，乙种货车最多可装帐篷和食品各20件．则民政局安排甲、乙两种货车时有几种方案？请你帮助设计出来．

(3)、在第（2）问的条件下，如果甲种货车每辆需付运输费4000元，乙种货车每辆需付运输费3600元．民政局应选择哪种方案可使运输费最少？最少运输费是多少元？

查看试题解析
22. 如图，点F在线段AB上，点E，G在线段CD上，AB∥CD，∠1=∠2．

(1)、求证：FG∥AE；

(2)、若FG⊥BC于点H，BC平分∠ABD，∠A=50°，求∠D的度数．

查看试题解析
23. 规定min（m，n）表示m，n中较小的数（m，n均为实数，且mn），例如：min{3，﹣1}＝﹣1，、min ${\sqrt{2} ， \sqrt{3}} = \sqrt{2}$ 据此解决下列问题：

(1)、min ${- \frac{1}{2} ， - \frac{1}{3}}$ ＝；

(2)、若min ${\frac{2 x - 1}{3} ， 2}$ ＝2，求x的取值范围；

(3)、若min{2x﹣5，x+3}＝﹣2，求x的值.

查看试题解析
24. 如图，直线AB $∥$ CD，直线 $E F$ 与 $A B$ 、 $C D$ 分别交于点 $G$ 、 $H$ ， $∠ E H D = α (0 ° < α < 90 °) .$ 小安将一个含 $30 °$ 角的直角三角板 $P M N$ 按如图①放置，使点 $N$ 、 $M$ 分别在直线 $A B$ 、 $C D$ 上，且在点 $G$ 、 $H$ 的右侧， $∠ P = 90 °$ ， $∠ P M N = 60 °$ ．

(1)、填空： $∠ P N B + ∠ P M D$ $∠ P$ （填“ $>$ ”“ $<$ ”或“ $=$ ”）；

(2)、若 $∠ M N G$ 的平分线 $N O$ 交直线 $C D$ 于点 $O$ ，如图②．
①当ON $∥$ EF，PM $∥$ EF时，求 $α$ 的度数；
②小安将三角板 $P M N$ 保持PM $∥$ EF并向左平移，在平移的过程中求 $∠ M O N$ 的度数（用含 $α$ 的式子表示）．

查看试题解析

类别	分数段	频数（人数）
A	60≤x＜70	a
B	70≤x＜80	16
C	80≤x＜90	24
D	90≤x＜100	6