山东省滨州市滨城区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-08 类型:期末考试
一、单选题
-
1. 冰墩墩是2022年北京冬季奥运会的吉祥物,将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,深受各国人们的欢迎.在下图中,将冰墩墩放入坐标系中,它盖住的点的坐标可能为( )
 A、 B、 C、 D、2. 如图所示,已知 , , , 则为( )
A、 B、 C、 D、2. 如图所示,已知 , , , 则为( ) A、 B、 C、 D、3. 下列调查中,适合采用抽样调查方法的是( )A、40名同学报考空军院校进行视力检查 B、检测中卫市的空气质量 C、为了解与新型冠状病毒确诊病人同时乘坐同一架飞机乘客的健康情况 D、为保证“神舟十三号”成功发射,对其零部件进行检查4. 如图,天平左盘中物体A的质量为 ,天平右盘中每个砝码的质量都是1g,则 的取值范围在数轴上可表示为( )
A、 B、 C、 D、3. 下列调查中,适合采用抽样调查方法的是( )A、40名同学报考空军院校进行视力检查 B、检测中卫市的空气质量 C、为了解与新型冠状病毒确诊病人同时乘坐同一架飞机乘客的健康情况 D、为保证“神舟十三号”成功发射,对其零部件进行检查4. 如图,天平左盘中物体A的质量为 ,天平右盘中每个砝码的质量都是1g,则 的取值范围在数轴上可表示为( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,将△ABC沿BC方向平移1cm得到对应的△A′B′C′.若B′C=2cm,则BC′的长是( )
5. 如图,将△ABC沿BC方向平移1cm得到对应的△A′B′C′.若B′C=2cm,则BC′的长是( ) A、2cm B、3cm C、4cm D、5cm6. 下列命题中,是真命题的是( )A、 B、过一点有且只有一条直线与已知直线垂直 C、点P在第四象限,且点P到x轴的距离为2,点P到y轴的距离为3,则点P的坐标为(3,-2) D、立方根等于它本身的数为7. 若一个正数m的两个平方根分别是3a+2和a-10,则m的立方根为( )A、-4 B、4 C、-2 D、28. 下列各数:3.1415926, , , , 其中是无理数的是( )A、3.1415926 B、 C、 D、9. 若 , 则下列不等式一定成立的是( ).A、 B、 C、 D、10. 解方程组时,一学生把看错而得到 , 而正确的解是 , 那么a+b+c的值为( )A、4 B、5 C、6 D、711. 把一些书分给几名同学,如果每人分 本,那么余 本;如果前面的每名同学分 本,那么最后一人就分不到 本,这些书有______本,共有______人.( )A、 本, 人 B、 本, 人 C、 本, 人 D、 本, 人12. 如图,长青化工厂与 , 两地有公路、铁路相连.这家工厂从地购买一批每吨1000元的原料运回工厂,制成每吨6000元的产品运到地.公路运价为1.6元 , 铁路运价为1.2元 , 这两次运输共支出公路运费16000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多( )元.
A、2cm B、3cm C、4cm D、5cm6. 下列命题中,是真命题的是( )A、 B、过一点有且只有一条直线与已知直线垂直 C、点P在第四象限,且点P到x轴的距离为2,点P到y轴的距离为3,则点P的坐标为(3,-2) D、立方根等于它本身的数为7. 若一个正数m的两个平方根分别是3a+2和a-10,则m的立方根为( )A、-4 B、4 C、-2 D、28. 下列各数:3.1415926, , , , 其中是无理数的是( )A、3.1415926 B、 C、 D、9. 若 , 则下列不等式一定成立的是( ).A、 B、 C、 D、10. 解方程组时,一学生把看错而得到 , 而正确的解是 , 那么a+b+c的值为( )A、4 B、5 C、6 D、711. 把一些书分给几名同学,如果每人分 本,那么余 本;如果前面的每名同学分 本,那么最后一人就分不到 本,这些书有______本,共有______人.( )A、 本, 人 B、 本, 人 C、 本, 人 D、 本, 人12. 如图,长青化工厂与 , 两地有公路、铁路相连.这家工厂从地购买一批每吨1000元的原料运回工厂,制成每吨6000元的产品运到地.公路运价为1.6元 , 铁路运价为1.2元 , 这两次运输共支出公路运费16000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多( )元. A、1286800 B、299000 C、1286000 D、298000
A、1286800 B、299000 C、1286000 D、298000二、填空题
-
13. 如图,直线a,b相交于点O,∠1=130°,则∠2的度数是 .
 14. 若第一象限内的点满足 , , 则点的坐标是 .15. 如图,点在的延长线上,下列条件:①;②;③;④;⑤ , 其中能判断的是 . (填写正确的序号即可)
14. 若第一象限内的点满足 , , 则点的坐标是 .15. 如图,点在的延长线上,下列条件:①;②;③;④;⑤ , 其中能判断的是 . (填写正确的序号即可) 16. 某班学生参加环保知识竞赛,已知竞赛得分都是整数,把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息可得,成绩不及格(低于60分)的学生占全班参赛人数的百分率是
16. 某班学生参加环保知识竞赛,已知竞赛得分都是整数,把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息可得,成绩不及格(低于60分)的学生占全班参赛人数的百分率是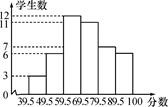 17. 若关于x、y的方程组的解为 , 则方程组的解是 .18. 若不等式组 的解集是 , 则m的取值范围是 .
17. 若关于x、y的方程组的解为 , 则方程组的解是 .18. 若不等式组 的解集是 , 则m的取值范围是 .三、解答题
-
19. 简答(1)、解不等式组: , 并把解集在数轴上表示出来.
 (2)、计算:20. 某校为了解疫情期间学生在家上网课的学习情况,随机抽取了该校部分学生对其学习效果进行调查,根据相关数据,绘制成以下不完整的统计图.
(2)、计算:20. 某校为了解疫情期间学生在家上网课的学习情况,随机抽取了该校部分学生对其学习效果进行调查,根据相关数据,绘制成以下不完整的统计图. (1)、此次调查该校学生人数为名,学习效果“较差”的部分对应的圆心角度数为;(2)、补全条形图;(3)、请估计该校3000名学生疫情期间网课学习效果“一般”的学生人数.21. 在四边形ABCD中,AB∥CD,AD∥BC,求证:
(1)、此次调查该校学生人数为名,学习效果“较差”的部分对应的圆心角度数为;(2)、补全条形图;(3)、请估计该校3000名学生疫情期间网课学习效果“一般”的学生人数.21. 在四边形ABCD中,AB∥CD,AD∥BC,求证: (1)、∠A+∠B+∠C+∠D=360°;(2)、∠A=∠C,∠B=∠D.22. 阅读材料,回答以下问题:
(1)、∠A+∠B+∠C+∠D=360°;(2)、∠A=∠C,∠B=∠D.22. 阅读材料,回答以下问题:我们知道,二元一次方程有无数个解,在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.例如是方程的一个解,对应点 , 如图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点 , , , , 将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程的解.所以,我们就把这条直线就叫做方程的图象.一般的,以任意二元一次方程解为坐标的对应点连成的直线就叫这个方程的图象.请问:
 (1)、已知、、 , 则点(填“或或”)在方程的图象上.(2)、求方程和方程图象的交点坐标.(3)、已知以关于、的方程组的解为坐标的点在方程的图象上,求的值.23. 某商店需要购进甲、乙两种商品共160件,其进价和售价如表:
(1)、已知、、 , 则点(填“或或”)在方程的图象上.(2)、求方程和方程图象的交点坐标.(3)、已知以关于、的方程组的解为坐标的点在方程的图象上,求的值.23. 某商店需要购进甲、乙两种商品共160件,其进价和售价如表:甲
乙
进价(元/件)
15
35
售价(元/件)
20
45
(1)、若商店计划销售完这批商品后能获利1100元.则甲、乙两种商品应分别购进多少件?(2)、若商店计划投入资金不多于4300元,且销售完这批商品获利多于1260元,商店有哪几种购货方案?哪种购货方案销售利润最大?请说明理由.24. 在平面直角坐标系中,已知点 , , , 且满足 , 线段交轴于点 , 点是轴正半轴上的一点. (1)、求出点A,B的坐标;(2)、如图2,若DBAC, , 且 , 分别平分 , , 求的度数;(用含的代数式表示).(3)、如图3,坐标轴上是否存在一点 , 使得的面积和的面积相等?若存在,求出点坐标;若不存在,请说明理由.
(1)、求出点A,B的坐标;(2)、如图2,若DBAC, , 且 , 分别平分 , , 求的度数;(用含的代数式表示).(3)、如图3,坐标轴上是否存在一点 , 使得的面积和的面积相等?若存在,求出点坐标;若不存在,请说明理由.