山东省东营市2022年中考数学真题
试卷更新日期:2022-09-08 类型:中考真卷
一、单选题
-
1. -2的绝对值是()
A、2 B、 C、 D、-22. 下列运算结果正确的是( )A、 B、 C、 D、3. 如图,直线 , 一个三角板的直角顶点在直线a上,两直角边均与直线b相交, , 则( )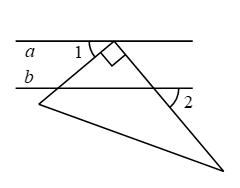 A、 B、 C、 D、4. 植树节当天,七年级1班植树300棵,正好占这批树苗总数的 , 七年级2班植树棵数是这批树苗总数的 , 则七年级2班植树的棵数是( )A、36 B、60 C、100 D、1805. 一元二次方程的解是( )A、 B、 C、 D、6. 如图,任意将图中的某一白色方块涂黑后,能使所有黑色方块构成的图形是轴对称图形的概率是( )
A、 B、 C、 D、4. 植树节当天,七年级1班植树300棵,正好占这批树苗总数的 , 七年级2班植树棵数是这批树苗总数的 , 则七年级2班植树的棵数是( )A、36 B、60 C、100 D、1805. 一元二次方程的解是( )A、 B、 C、 D、6. 如图,任意将图中的某一白色方块涂黑后,能使所有黑色方块构成的图形是轴对称图形的概率是( ) A、 B、 C、 D、7. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A、 B、 C、 D、7. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、8. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )
A、 B、 C、 D、8. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )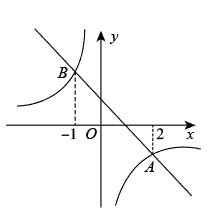 A、或 B、或 C、或 D、9. 用一张半圆形铁皮,围成一个底面半径为的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为( )A、 B、 C、 D、10. 如图,已知菱形的边长为2,对角线相交于点O,点M,N分别是边上的动点, , 连接.以下四个结论正确的是( )
A、或 B、或 C、或 D、9. 用一张半圆形铁皮,围成一个底面半径为的圆锥形工件的侧面(接缝忽略不计),则圆锥的母线长为( )A、 B、 C、 D、10. 如图,已知菱形的边长为2,对角线相交于点O,点M,N分别是边上的动点, , 连接.以下四个结论正确的是( )
①是等边三角形;②的最小值是;③当最小时;④当时,.
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
11. 2022年2月20日,北京冬奥会圆满落幕,赛事获得了数十亿次数字平台互动,在中国仅电视收视人数就超6亿.6亿用科学记数法表示为.12. 因式分解: .13. 为了落实“双减”政策,东营市某学校对初中学生的课外作业时长进行了问卷调查,15名同学的作业时长统计如下表,则这组数据的众数是分钟.
作业时长(单位:分钟)
50
60
70
80
90
人数(单位:人)
1
4
6
2
2
14. 如图,在中,弦半径 , 则的度数为 .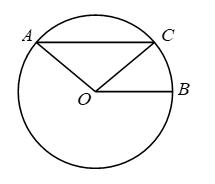 15. 关于x的一元二次方程有两个不相等的实数根,则k的取值范围是 .16. 如图,是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数的图象上,则经过点A的反比例函数表达式为 .
15. 关于x的一元二次方程有两个不相等的实数根,则k的取值范围是 .16. 如图,是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数的图象上,则经过点A的反比例函数表达式为 .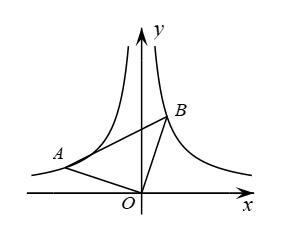 17. 如图,在中,点F、G在上,点E、H分别在、上,四边形是矩形,是的高. , 那么的长为 .
17. 如图,在中,点F、G在上,点E、H分别在、上,四边形是矩形,是的高. , 那么的长为 .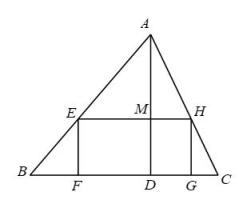 18. 如图,是等边三角形,直线经过它们的顶点 , 点在x轴上,则点的横坐标是.
18. 如图,是等边三角形,直线经过它们的顶点 , 点在x轴上,则点的横坐标是.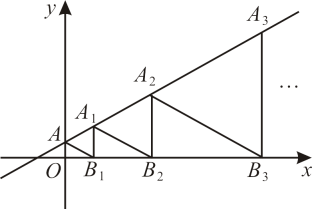
三、解答题
-
19. 计算及先化简,再求值:(1)、(2)、 , 其中.20. 中国共产党的助手和后备军——中国共青团,担负着为中国特色社会主义事业培养合格建设者和可靠接班人的根本任务.成立一百周年之际,各中学持续开展了A:青年大学习;B:背年学党史;C:中国梦宣传教育;D:社会主义核心价值观培育践行等一系列活动,学生可以任选一项参加.为了解参与情况,进行了一次抽样调查,根据收集的数据绘制了两幅不完整的统计图.
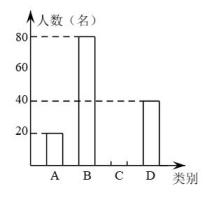
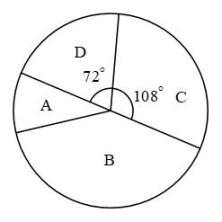
请根据图中提供的信息,解答下列问题:
(1)、在这次调查中,一共抽取了名学生;(2)、补全条形统计图;(3)、若该校共有学生1280名,请估计参加B项活动的学生数;(4)、小杰和小慧参加了上述活动,请用列表或画树状图的方法,求他们参加同一项活动的概率.21. 如图,为的直径,点C为上一点,于点D,平分 .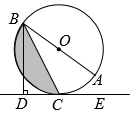 (1)、求证:直线是的切线;(2)、若的半径为2,求图中阴影部分的面积.22. 胜利黄河大桥犹如一架巨大的竖琴,凌驾于滔滔黄河之上,使黄河南北“天堑变通途”.已知主塔垂直于桥面于点B,其中两条斜拉索与桥面的夹角分别为和 , 两固定点D、C之间的距离约为 , 求主塔的高度(结果保留整数,参考数据:)
(1)、求证:直线是的切线;(2)、若的半径为2,求图中阴影部分的面积.22. 胜利黄河大桥犹如一架巨大的竖琴,凌驾于滔滔黄河之上,使黄河南北“天堑变通途”.已知主塔垂直于桥面于点B,其中两条斜拉索与桥面的夹角分别为和 , 两固定点D、C之间的距离约为 , 求主塔的高度(结果保留整数,参考数据:) 23. 为满足顾客的购物需求,某水果店计划购进甲、乙两种水果进行销售.经了解,甲水果的进价比乙水果的进价低20%,水果店用1000元购进甲种水果比用1200元购进乙种水果的重量多10千克,已知甲,乙两种水果的售价分别为6元/千克和8元/千克.(1)、求甲、乙两种水果的进价分别是多少?(2)、若水果店购进这两种水果共150千克,其中甲种水果的重量不低于乙种水果重量的2倍,则水果店应如何进货才能获得最大利润,最大利润是多少?24. 如图,抛物线与x轴交于点 , 点 , 与y轴交于点C.
23. 为满足顾客的购物需求,某水果店计划购进甲、乙两种水果进行销售.经了解,甲水果的进价比乙水果的进价低20%,水果店用1000元购进甲种水果比用1200元购进乙种水果的重量多10千克,已知甲,乙两种水果的售价分别为6元/千克和8元/千克.(1)、求甲、乙两种水果的进价分别是多少?(2)、若水果店购进这两种水果共150千克,其中甲种水果的重量不低于乙种水果重量的2倍,则水果店应如何进货才能获得最大利润,最大利润是多少?24. 如图,抛物线与x轴交于点 , 点 , 与y轴交于点C.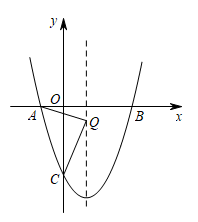 (1)、求抛物线的表达式;(2)、在对称轴上找一点Q,使的周长最小,求点Q的坐标;(3)、点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.25. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.
(1)、求抛物线的表达式;(2)、在对称轴上找一点Q,使的周长最小,求点Q的坐标;(3)、点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.25. 和均为等边三角形,点E、D分别从点A,B同时出发,以相同的速度沿运动,运动到点B、C停止.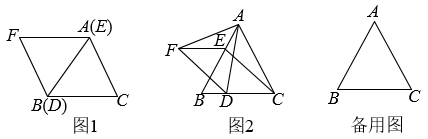 (1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.
(1)、如图1,当点E、D分别与点A、B重合时,请判断:线段的数量关系是 , 位置关系是;(2)、如图2,当点E、D不与点A,B重合时,(1)中的结论是否依然成立?若成立,请给予证明;若不成立,请说明理由;(3)、当点D运动到什么位置时,四边形的面积是面积的一半,请直接写出答案;此时,四边形是哪种特殊四边形?请在备用图中画出图形并给予证明.