辽宁省朝阳市2022年中考数学真题
试卷更新日期:2022-09-08 类型:中考真卷
一、单选题
-
1. 2022的倒数是( ).A、 B、 C、2022 D、-20222. 如图所示的几何体是由5个大小相同的小立方块搭成的,它的主视图是( )
 A、
A、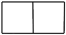 B、
B、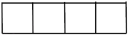 C、
C、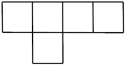 D、
D、 3. 如图所示的是由8个全等的小正方形组成的图案,假设可以随意在图中取一点,那么这个点取在阴影部分的概率是( )
3. 如图所示的是由8个全等的小正方形组成的图案,假设可以随意在图中取一点,那么这个点取在阴影部分的概率是( )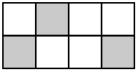 A、 B、 C、 D、14. 下列运算正确的是( )A、a8÷a4=a2 B、4a5﹣3a5=1 C、a3•a4=a7 D、(a2)4=a65. 将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上,∠EFG=90°,∠EGF=60°,∠AEF=50°,则∠EGC的度数为( )
A、 B、 C、 D、14. 下列运算正确的是( )A、a8÷a4=a2 B、4a5﹣3a5=1 C、a3•a4=a7 D、(a2)4=a65. 将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上,∠EFG=90°,∠EGF=60°,∠AEF=50°,则∠EGC的度数为( )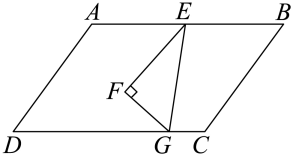 A、100° B、80° C、70° D、60°6. 新冠肺炎疫情期间,学校要求学生每天早晨入校前在家测量体温,七年三班第二学习小组6名同学某天的体温(单位:℃)记录如下:36.1,36.2,36.0,36.0,36.1,36.1.则这组数据的中位数和众数分别是( )A、36.0,36.1 B、36.1,36.0 C、36.2,36.1 D、36.1,36.17. 如图,在⊙O中,点A是的中点,∠ADC=24°,则∠AOB的度数是( )
A、100° B、80° C、70° D、60°6. 新冠肺炎疫情期间,学校要求学生每天早晨入校前在家测量体温,七年三班第二学习小组6名同学某天的体温(单位:℃)记录如下:36.1,36.2,36.0,36.0,36.1,36.1.则这组数据的中位数和众数分别是( )A、36.0,36.1 B、36.1,36.0 C、36.2,36.1 D、36.1,36.17. 如图,在⊙O中,点A是的中点,∠ADC=24°,则∠AOB的度数是( )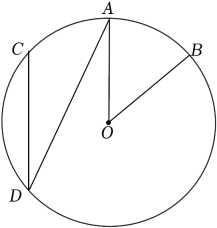 A、24° B、26° C、48° D、66°8. 如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )
A、24° B、26° C、48° D、66°8. 如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )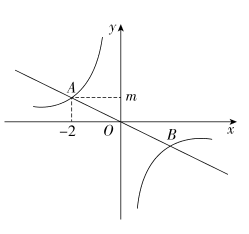 A、x<﹣2或x>2 B、﹣2<x<2 C、﹣2<x<0或x>2 D、x<﹣2或0<x<29. 八年一班学生周末乘车去红色教育基地参观学习,基地距学校60km,一部分学生乘慢车先行,出发30min后,另一部分学生乘快车前往,结果同时到达.已知快车的速度是慢车速度的1.5倍,求慢车的速度.设慢车每小时行驶xkm,根据题意,所列方程正确的是( )A、﹣= B、﹣= C、﹣=30 D、﹣=3010. 如图,二次函数y=ax2+bx+c(a为常数,且a≠0)的图象过点(﹣1,0),对称轴为直线x=1,且2<c<3,则下列结论正确的是( )
A、x<﹣2或x>2 B、﹣2<x<2 C、﹣2<x<0或x>2 D、x<﹣2或0<x<29. 八年一班学生周末乘车去红色教育基地参观学习,基地距学校60km,一部分学生乘慢车先行,出发30min后,另一部分学生乘快车前往,结果同时到达.已知快车的速度是慢车速度的1.5倍,求慢车的速度.设慢车每小时行驶xkm,根据题意,所列方程正确的是( )A、﹣= B、﹣= C、﹣=30 D、﹣=3010. 如图,二次函数y=ax2+bx+c(a为常数,且a≠0)的图象过点(﹣1,0),对称轴为直线x=1,且2<c<3,则下列结论正确的是( )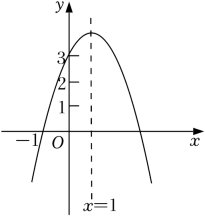 A、abc>0 B、3a+c>0 C、a2m2+abm≤a2+ab(m为任意实数) D、﹣1<a<﹣
A、abc>0 B、3a+c>0 C、a2m2+abm≤a2+ab(m为任意实数) D、﹣1<a<﹣二、填空题
-
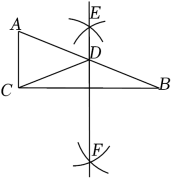
11. 光在真空中1s传播299792km.数据299792用科学记数法表示为 .12. 甲、乙、丙、丁四名同学参加掷实心球测试,每人掷5次,他们的平均成绩恰好相同,方差分别是s甲2=0.55,s乙2=0.56,s丙2=0.52,s丁2=0.48,则这四名同学掷实心球的成绩最稳定的是 .13. 计算:= .14. 如图,在RtABC中,∠ACB=90°,AB=13,BC=12,分别以点B和点C为圆心、大于BC的长为半径作弧,两弧相交于E,F两点,作直线EF交AB于点D,连接CD,则ACD的周长是 .
 15. 如图,在矩形ABCD中,AD=2 , DC=4 , 将线段DC绕点D按逆时针方向旋转,当点C的对应点E恰好落在边AB上时,图中阴影部分的面积是 .
15. 如图,在矩形ABCD中,AD=2 , DC=4 , 将线段DC绕点D按逆时针方向旋转,当点C的对应点E恰好落在边AB上时,图中阴影部分的面积是 .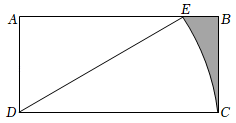 16. 等边三角形ABC中,D是边BC上的一点,BD=2CD,以AD为边作等边三角形ADE,连接CE.若CE=2,则等边三角形ABC的边长为 .
16. 等边三角形ABC中,D是边BC上的一点,BD=2CD,以AD为边作等边三角形ADE,连接CE.若CE=2,则等边三角形ABC的边长为 .三、解答题
-
17. 先化简,简求值: , 其中 .18. 某中学要为体育社团购买一些篮球和排球,若购买3个篮球和2个排球,共需560元;若购买2个篮球和4个排球,共需640元.(1)、求每个篮球和每个排球的价格分别是多少元;(2)、该中学决定购买篮球和排球共10个,总费用不超过1100元,那么最多可以购买多少个篮球?19. 为了解学生的睡眠情况,某校随机抽取部分学生对他们最近两周的睡眠情况进行调查,得到他们每日平均睡眠时长x(单位:h)的一组数据,将所得数据分为四组(A:x<8;B:8≤x<9;C:9≤x<10;D:x≥10),并绘制成如下两幅不完整的统计图.
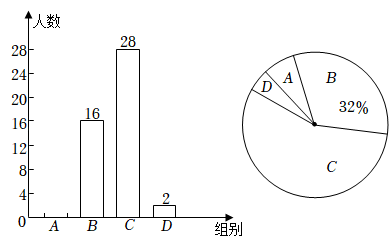
根据以上信息,解答下列问题:
(1)、本次一共抽样调查了名学生.(2)、求出扇形统计图中D组所对应的扇形圆心角的度数.(3)、将条形统计图补充完整.(4)、若该校共有1200名学生,请估计最近两周有多少名学生的每日平均睡眠时长大于或等于9h.20. 某社区组织A,B,C,D四个小区的居民进行核酸检测,有很多志愿者参与此项检测工作,志愿者王明和李丽分别被随机安排到这四个小区中的一个小区组织居民排队等候.(1)、王明被安排到A小区进行服务的概率是 .(2)、请用列表法或画树状图法求出王明和李丽被安排到同一个小区工作的概率.21. 某数学兴趣小组准备测量校园内旗杆顶端到地面的高度(旗杆底端有台阶).该小组在C处安置测角仪CD,测得旗杆顶端A的仰角为30°,前进8m到达E处,安置测角仪EF,测得旗杆顶端A的仰角为45°(点B,E,C在同一直线上),测角仪支架高CD=EF=1.2m,求旗杆顶端A到地面的距离即AB的长度.(结果精确到1m.参考数据:≈1.7)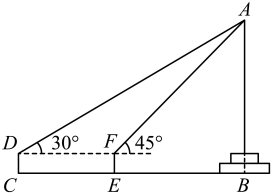 22. 如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.
22. 如图,AC是⊙O的直径,弦BD交AC于点E,点F为BD延长线上一点,∠DAF=∠B.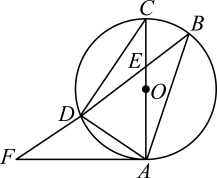 (1)、求证:AF是⊙O的切线;(2)、若⊙O的半径为5,AD是AEF的中线,且AD=6,求AE的长.23. 某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.(1)、求y与x之间的函数关系式.(2)、若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?(3)、设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?24. 【思维探究】如图1,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,连接AC.求证:BC+CD=AC.
(1)、求证:AF是⊙O的切线;(2)、若⊙O的半径为5,AD是AEF的中线,且AD=6,求AE的长.23. 某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.(1)、求y与x之间的函数关系式.(2)、若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?(3)、设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?24. 【思维探究】如图1,在四边形ABCD中,∠BAD=60°,∠BCD=120°,AB=AD,连接AC.求证:BC+CD=AC.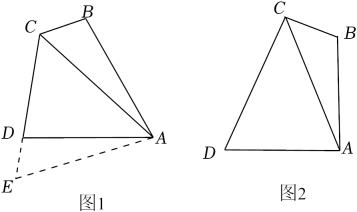 (1)、小明的思路是:延长CD到点E,使DE=BC,连接AE.根据∠BAD+∠BCD=180°,推得∠B+∠ADC=180°,从而得到∠B=∠ADE,然后证明ADE≌ABC,从而可证BC+CD=AC,请你帮助小明写出完整的证明过程.(2)、【思维延伸】如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,猜想BC,CD,AC之间的数量关系,并说明理由.(3)、【思维拓展】在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD= , AC与BD相交于点O.若四边形ABCD中有一个内角是75°,请直接写出线段OD的长.25. 如图,在平面直角坐标系中,抛物线与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.
(1)、小明的思路是:延长CD到点E,使DE=BC,连接AE.根据∠BAD+∠BCD=180°,推得∠B+∠ADC=180°,从而得到∠B=∠ADE,然后证明ADE≌ABC,从而可证BC+CD=AC,请你帮助小明写出完整的证明过程.(2)、【思维延伸】如图2,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,连接AC,猜想BC,CD,AC之间的数量关系,并说明理由.(3)、【思维拓展】在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD= , AC与BD相交于点O.若四边形ABCD中有一个内角是75°,请直接写出线段OD的长.25. 如图,在平面直角坐标系中,抛物线与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.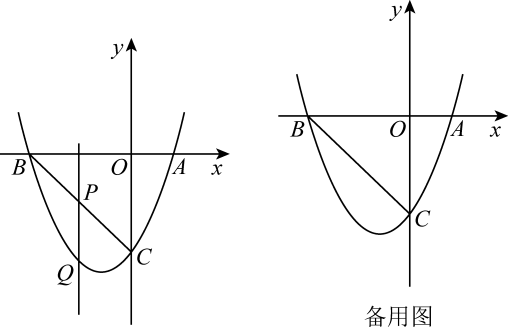 (1)、求抛物线的解析式及点B的坐标.(2)、如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.(3)、动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式及点B的坐标.(2)、如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.(3)、动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.