辽宁省鞍山市2022年中考数学真题
试卷更新日期:2022-09-08 类型:中考真卷
一、单选题
-
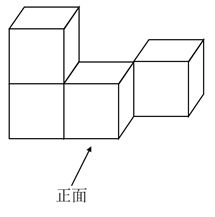
1. 2022的相反数是( )A、 B、 C、−2022 D、20222. 如图所示的几何体是由4个大小相同的小正方体搭成的,它的左视图是( )
 A、
A、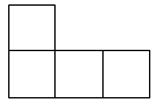 B、
B、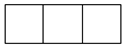 C、
C、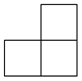 D、
D、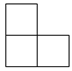 3. 下列运算正确的是( )A、 B、 C、 D、4. 为了解居民用水情况,小丽在自家居住的小区随机抽查了10户家庭月用水量,统计如下表:
3. 下列运算正确的是( )A、 B、 C、 D、4. 为了解居民用水情况,小丽在自家居住的小区随机抽查了10户家庭月用水量,统计如下表:月用水量/
7
8
9
10
户数
2
3
4
1
则这10户家庭的月用水量的众数和中位数分别是( )
A、8,7.5 B、8,8.5 C、9,8.5 D、9,7.55. 如图,直线 , 等边三角形的顶点在直线上, , 则的度数为( )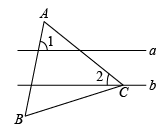 A、 B、 C、 D、6. 如图,在中, , , 延长到点 , 使 , 连接 , 则的度数( )
A、 B、 C、 D、6. 如图,在中, , , 延长到点 , 使 , 连接 , 则的度数( )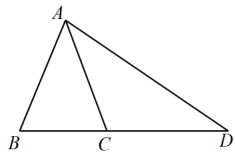 A、 B、 C、 D、7. 如图,在矩形中, , , 以点为圆心,长为半径画弧,交于点 , 连接 , 则扇形的面积为( )
A、 B、 C、 D、7. 如图,在矩形中, , , 以点为圆心,长为半径画弧,交于点 , 连接 , 则扇形的面积为( )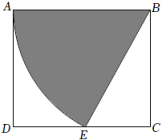 A、 B、 C、 D、8. 如图,在中, , , , , 垂足为点 , 动点从点出发沿方向以的速度匀速运动到点 , 同时动点从点出发沿射线方向以的速度匀速运动.当点停止运动时,点也随之停止,连接 , 设运动时间为 , 的面积为 , 则下列图象能大致反映与之间函数关系的是( )
A、 B、 C、 D、8. 如图,在中, , , , , 垂足为点 , 动点从点出发沿方向以的速度匀速运动到点 , 同时动点从点出发沿射线方向以的速度匀速运动.当点停止运动时,点也随之停止,连接 , 设运动时间为 , 的面积为 , 则下列图象能大致反映与之间函数关系的是( ) A、
A、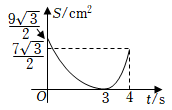 B、
B、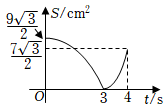 C、
C、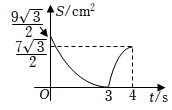 D、
D、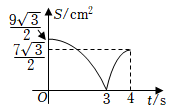
二、填空题
-
9. 教育部2022年5月17日召开第二场“教育这十年”“1+1”系列新闻发布会,会上介绍我国已建成世界最大规模高等教育体系,在学总人数超过44300000人.将数据44300000用科学记数法表示为 .10. 一个不透明的口袋中装有5个红球和个黄球,这些球除颜色外都相同,某同学进行了如下试验:从袋中随机摸出1个球记下它的颜色后,放回摇匀,为一次摸球试验.根据记录在下表中的摸球试验数据,可以估计出的值为 .
摸球的总次数
100
500
1000
2000
…
摸出红球的次数
19
101
199
400
…
摸出红球的频率
0.190
0.202
0.199
0.200
…
11. 如图, , , 相交于点 , 若 , , 则的长为 .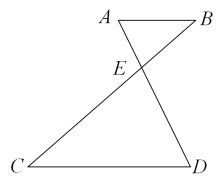 12. 某加工厂接到一笔订单,甲、乙车间同时加工,已知乙车间每天加工的产品数量是甲车间每天加工的产品数量的1.5倍,甲车间加工4000件比乙车间加工4200件多用3天.设甲车间每天加工件产品,根据题意可列方程为 .13. 如图,在中, , , , 点 , 分别在 , 上,将沿直线翻折,点的对应点恰好落在上,连接 , 若 , 则的长为 .
12. 某加工厂接到一笔订单,甲、乙车间同时加工,已知乙车间每天加工的产品数量是甲车间每天加工的产品数量的1.5倍,甲车间加工4000件比乙车间加工4200件多用3天.设甲车间每天加工件产品,根据题意可列方程为 .13. 如图,在中, , , , 点 , 分别在 , 上,将沿直线翻折,点的对应点恰好落在上,连接 , 若 , 则的长为 .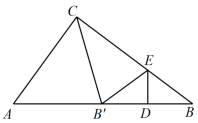 14. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .
14. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .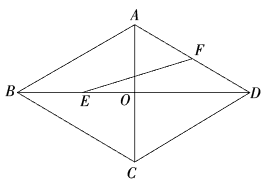 15. 如图,在平面直角坐标系中,是坐标原点.在中, , 边在轴上,点是边上一点,且 , 反比例函数的图象经过点交于点 , 连接 . 若 , 则的值为 .
15. 如图,在平面直角坐标系中,是坐标原点.在中, , 边在轴上,点是边上一点,且 , 反比例函数的图象经过点交于点 , 连接 . 若 , 则的值为 . 16. 如图,在正方形中,点为的中点, , 交于点 , 于点 , 平分 , 分别交 , 于点 , , 延长交于点 , 连接 . 下列结论:①;②;③;④ . 其中正确的是 . (填序号即可).
16. 如图,在正方形中,点为的中点, , 交于点 , 于点 , 平分 , 分别交 , 于点 , , 延长交于点 , 连接 . 下列结论:①;②;③;④ . 其中正确的是 . (填序号即可).
三、解答题
-
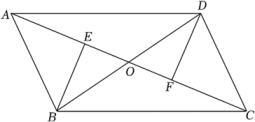
17. 先化简,再求值: ,其中 .18. 如图,在四边形中,与交于点 , , , 垂足分别为点 , , 且 , . 求证:四边形是平行四边形.
 19. 某校开展“凝心聚力颂家乡”系列活动,组建了四个活动小组供学生参加:(朗诵),(绘画),(唱歌),(征文),学校规定:每名学生都必须参加且只能参加其中一个活动小组.学校随机抽取了部分学生,对其参加活动小组情况进行了调查.根据调查结果绘制成如下两幅不完整的统计图(图1和图2).
19. 某校开展“凝心聚力颂家乡”系列活动,组建了四个活动小组供学生参加:(朗诵),(绘画),(唱歌),(征文),学校规定:每名学生都必须参加且只能参加其中一个活动小组.学校随机抽取了部分学生,对其参加活动小组情况进行了调查.根据调查结果绘制成如下两幅不完整的统计图(图1和图2).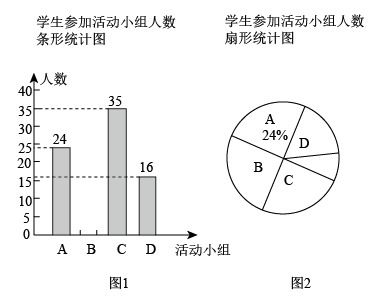
请根据统计图提供的信息,解答下列问题:
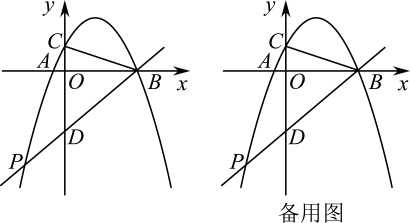
(1)、本次共调查了名学生,扇形统计图中“”对应的圆心角度数为 .(2)、请补全条形统计图.(3)、若该校共有2000名学生,根据调查结果,请你估计这所学校参加活动小组的学生人数.20. 2022年4月15日是第七个全民国家安全教育日,某校七、八年级举行了一次国家安全知识竞赛,经过评比后,七年级的两名学生(用 , 表示)和八年级的两名学生(用 , 表示)获得优秀奖.(1)、从获得优秀奖的学生中随机抽取一名分享经验,恰好抽到七年级学生的概率是 .(2)、从获得优秀奖的学生中随机抽取两名分享经验,请用列表法或画树状图法,求抽取的两名学生恰好一名来自七年级、一名来自八年级的概率.21. 北京时间2022年4月16日9时56分,神舟十三号载人飞船返回舱成功着陆.为弘扬航天精神,某校在教学楼上悬挂了一幅长为的励志条幅(即).小亮同学想知道条幅的底端到地面的距离,他的测量过程如下:如图,首先他站在楼前点处,在点正上方点处测得条幅顶端的仰角为 , 然后向教学楼条幅方向前行到达点处(楼底部点与点 , 在一条直线上),在点正上方点处测得条幅底端的仰角为 , 若 , 均为(即四边形为矩形),请你帮助小亮计算条幅底端到地面的距离的长度.(结果精确到 , 参考数据: , , )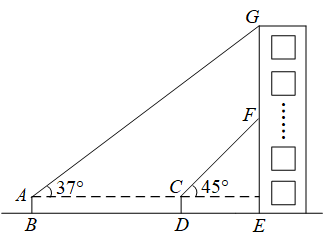 22. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点 , 与轴交于点 .
22. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点 , 与轴交于点 .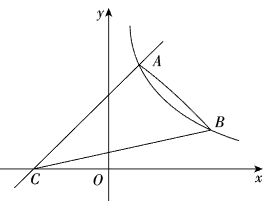 (1)、求点的坐标和反比例函数的解析式;(2)、点是反比例函数图象上一点且纵坐标是1,连接 , , 求的面积.23. 如图,是的外接圆,为的直径,点为上一点,交的延长线于点 , 与交于点 , 连接 , 若 .
(1)、求点的坐标和反比例函数的解析式;(2)、点是反比例函数图象上一点且纵坐标是1,连接 , , 求的面积.23. 如图,是的外接圆,为的直径,点为上一点,交的延长线于点 , 与交于点 , 连接 , 若 .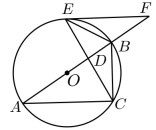 (1)、求证:是的切线.(2)、若 , , 求的半径.24. 某超市购进一批水果,成本为8元/ , 根据市场调研发现,这种水果在未来10天的售价(元/)与时间第天之间满足函数关系式( , 为整数),又通过分析销售情况,发现每天销售量与时间第天之间满足一次函数关系,下表是其中的三组对应值.
(1)、求证:是的切线.(2)、若 , , 求的半径.24. 某超市购进一批水果,成本为8元/ , 根据市场调研发现,这种水果在未来10天的售价(元/)与时间第天之间满足函数关系式( , 为整数),又通过分析销售情况,发现每天销售量与时间第天之间满足一次函数关系,下表是其中的三组对应值.时间第天
…
2
5
9
…
销售量
…
33
30
26
…
(1)、求与的函数解析式;(2)、在这10天中,哪一天销售这种水果的利润最大,最大销售利润为多少元?