辽宁省营口市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-09-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数是无理数的是（）

A、 $\sqrt{9}$ B、 $\sqrt{2}$ C、 $| - 2 |$ D、 $\frac{1}{3}$

查看试题解析
2. 在下列结论中，正确的是（）

A、 $\sqrt{\frac{25}{16}} = \pm \frac{5}{4}$ B、 $- 3$ 没有立方根 C、平方根是它本身的数为0， $± 1$ D、 $\sqrt{64}$ 的立方根是2

查看试题解析
3. 如图，直线AB、CD相交于点O，OE⊥AB于O，∠EOC=35°，则∠AOD的度数为

A、125° B、115 C、55° D、35°

查看试题解析

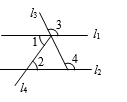
4. 某同学的作业如下框，其中※处填的依据是（）

如图，已知直线 $l_{1} ， l_{2} ， l_{3} ， l_{4}$ .若 $∠ 1 = ∠ 2$ ，则 $∠ 3 = ∠ 4$ .

请完成下面的说理过程.

解：已知 $∠ 1 = ∠ 2$ ，

根据（内错角相等，两直线平行），得 $l_{1} // l_{2}$ .

再根据（ ※ ），得 $∠ 3 = ∠ 4$ .

A、两直线平行，内错角相等 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，同旁内角互补

查看试题解析

5. 在下列调查中，适宜采用全面调查的是（）

A、了解辽宁省所有中学生的视力情况 B、了解某校七（4）班学生校服的尺码情况 C、了解某市居民日平均用水量情况 D、调查中国“2022冬奥会开幕式”节目的收视率

查看试题解析
6. 下列说法错误的是（）

A、x轴上的点的纵坐标为0 B、点 $P (- 1 ， 3)$ 到y轴的距离是1 C、若点 $A (- a - 1 ， 2)$ 在第二象限，那么 $a > - 1$ D、若 $x y < 0$ ，那么点 $Q (x ， y)$ 在第四象限

查看试题解析
7. 平面直角坐标系中，点 $A (- 5 ， 6)$ ， $B (3 ， - 4)$ ，经过点A的直线a与x轴平行，如果点C是直线a上的一个动点，那么当线段 $B C$ 的长度最短时，点C的坐标为（）

A、 $(6 ， - 3)$ B、 $(- 4 ， - 5)$ C、 $(3 ， 6)$ D、 $(- 5 ， - 4)$

查看试题解析
8. 由 $\frac{x}{3} - \frac{y}{2} = 1$ 可以得到用x表示y的式子为（）

A、 $y = \frac{2 x - 2}{3}$ B、 $y = - \frac{2 x - 1}{3}$ C、 $y = \frac{2 x}{3} - 2$ D、 $y = 2 - \frac{2 x}{3}$

查看试题解析
9. 我国古代数学著作《孙子算经》有“多人共车”问题：“今有三人共车，二车空；二人共车，九人步，问：人与车各几何？”其大意如下：有若干人要坐车，如果每3人坐一辆车，那么有2辆空车；如果每2人坐一辆车，那么有9人需要步行，问人与车各多少？设共有x人，y辆车，则可列方程组为（　　）

A、 ${\begin{array}{l} 3 (y - 2) = x \\ 2 y - 9 = x \end{array}$ B、 ${\begin{array}{l} 3 (y + 2) = x \\ 2 y + 9 = x \end{array}$ C、 ${\begin{array}{l} 3 (y - 2) = x \\ 2 y + 9 = x \end{array}$ D、 ${\begin{array}{l} 3 (y + 2) = x \\ 2 y - 9 = x \end{array}$

查看试题解析
10. 如图， $Δ A B C$ 是直角三角形，它的直角边 $A B = 6$ ， $B C = 8$ ，将 $Δ A B C$ 沿边BC的方向平移到 $Δ D E F$ 的位置，DE交AC于点G， $B E = 2$ ， $Δ C E G$ 的面积为13.5，下列结论：① $Δ A B C$ 平移的距离是4：② $D G = 1.5$ ；③AD $∥$ CF；④四边形ADFC的面积为6．其中正确的结论是（）

A、①② B、②③ C、③④ D、②④

查看试题解析

二、填空题

11. $- 3$ 的相反数是.

查看试题解析
12. 比较大小： $\sqrt[3]{- 25}$ $- 3$ .（填“ $>$ ”“ $<$ ”或“ $=$ ”)

查看试题解析
13. 已知点P的坐标为 $(2 - a, 6)$ ，且点P到两坐标轴的距离相等，则a的值为．

查看试题解析
14. 如图， $A B = 3 c m$ ， $B C = 4 c m$ ， $A C = 2 c m$ ，将 $△ A B C$ 沿BC方向平移 $2.5 c m$ ，得到 $△ D E F$ ，连接AD，则阴影部分的周长为cm．

查看试题解析
15. 把“对顶角相等”改写成“如果…那么…”的形式．

查看试题解析
16. 已知一个40个数据的样本，把它分成6组，第一组到第四组的频数分别是10、5、7、6，第五组的频率是0.2，那么第六组的频数是．

查看试题解析
17. 若（3x﹣y+5）²+|2x﹣y+3|＝0，则x﹣y的值为．

查看试题解析
18. 商店为了对某种商品促销，将定价为3元的商品，以下列方式优惠销售：若购买不超过5件，按原价付款；若一次性购买5件以上，超过部分打八折．现有27元钱，最多可以购买该商品的件数是．

查看试题解析

三、解答题

19. 为了提高农田利用效益，某地由每年种植双季稻改为先养殖小龙虾再种植一季水稻的“虾·稻”轮作模式，某农户有农田20亩，去年开始实施“虾·稻”轮作，去年出售小龙虾每千克获得的利润为 $32$ 元（利润＝售价－成本）．由于开发成本下降和市场供求关系变化，今年每千克小龙虾的养殖成本下降 $25 %$ ，售价下降 $10 %$ ，出售小龙虾每千克获得利润为 $30$ 元．

(1)、求去年每千克小龙虾的养殖成本与售价；

(2)、该农户今年每亩农田收获小龙虾100千克，若今年的水稻种植成本为 $600$ 元/亩，稻谷售价为 $2.5$ 元/千克，该农户估计今年可获得“虾·稻”轮作收入不少于 $8$ 万元，则稻谷的亩产量至少会达到多少千克？

查看试题解析
20. 计算

(1)、 $\sqrt{18} - \sqrt[3]{- 8} + | \sqrt{2} - 2 |$ ．

(2)、当x为何值时，代数式 $\frac{2 x - 1}{3} - \frac{5 x + 1}{2} - 1$ 的值是非负数？

(3)、解不等式组： ${\begin{array}{l} 5 x - 2 > 3 (x + 1) \\ \frac{1}{2} x - 1 ⩽ 7 - \frac{3}{2} x \end{array}$

查看试题解析
21. 已知方程组 ${\begin{array}{l} 5 x + y = 3 \\ a x + 5 y = 4 \end{array}$ 和 ${\begin{array}{l} x - 2 y = 5 \\ 5 x + b y = 1 \end{array}$ 有相同的解，求 $a - 5 b$ 的平方根．

查看试题解析
22. 如图，四边形ABCD中AB $∥$ CD，在BC的延长线上取一点E，连接AE交CD于点F，且满足 $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ．求证：AD $∥$ BE

查看试题解析
23. 某地区为了了解七年级学生防疫知识的掌握情况，从该地区七年级学生中随机抽取部分学生进行防疫知识测试，并把学生的得分绘制了部分频数分布表和频数分布直方图（如图）．已知图中从左到右第一、第二、第三、第四小组的频数的比为1∶3∶4∶2．
分组
频数
$60 ⩽ x < 70$
$70 ⩽ x < 80$
15
$80 ⩽ x < 90$
$90 ⩽ x < 100$

(1)、此次活动共抽取了多少名学生进行防疫知识测试？

(2)、请将表补充完整．

(3)、如果该地区七年级共有6000名学生，80分以上（含80分）的成绩为掌握防疫知识比较好，请估计该地区七年级有多少名学生掌握防疫知识比较好．

查看试题解析
24. 为实施“十四五”清洁生产推行方案，开展清洁生产改造，某工厂投资组建了日废水处理量为m吨的废水处理车间对该厂工业废水进行无害化处理．但随着工厂生产规模的扩大，该车间经常无法完成当天工业废水的处理任务，需要将超出日废水处理量的废水交给第三方企业处理．已知该车间处理废水，每天需固定成本40元，并且每处理一吨废水还需其他费用5元；将废水交给第三方企业处理，每吨需支付9元．根据记录，6月21日，该厂产生工业废水40吨，共花费废水处理费280元．

(1)、求该车间的日废水处理量m；

(2)、为实现可持续发展，走绿色发展之路，工厂合理控制了生产规模，使得每天废水处理的平均费用不超过7元/吨，试计算该厂一天产生的工业废水量的范围．

查看试题解析
25. 如图，在平面直角坐标系中，四边形ABCD为长方形，其中点A和点C的坐标分别为 $(- 4 ， 2)$ ， $(1 ， - 4)$ ，且AD $∥$ x轴，交y轴于点M，AB交x轴于点N．

(1)、直接写出点B的坐标； $∠ O B C$ 的度数为．

(2)、若动点P从点A出发，沿AB向点B运动，在点P运动过程中，连接MP，OP，试探究 $∠ A M P$ ， $∠ M P O$ ， $∠ P O N$ 之间的数量关系，并说明理由．

(3)、若动点P从点A出发，沿AB→BC→CD以每秒0.25个单位长度的速度向终点D匀速运动，设点P的运动时间为t秒，当 $△ A M P$ 的面积大于长方形ABCD面积的 $\frac{1}{3}$ 时，直接写出时间t的取值范围．

查看试题解析

分组	频数
$60 ⩽ x < 70$
$70 ⩽ x < 80$	15
$80 ⩽ x < 90$
$90 ⩽ x < 100$