辽宁省沈阳市浑南区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
1. 下面是沈阳、大连、青岛、济南四个城市的地铁图标,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 已知空气的单位体积质量是 , 将数据0.001239用科学记数法表示为( )A、 B、 C、 D、4. 如图,直线a和b被直线c所截,下列条件中不能判断a∥b的是( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 已知空气的单位体积质量是 , 将数据0.001239用科学记数法表示为( )A、 B、 C、 D、4. 如图,直线a和b被直线c所截,下列条件中不能判断a∥b的是( )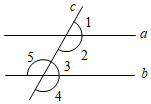 A、∠1=∠3 B、∠2=∠5 C、∠2+∠4=180° D、∠2+∠3=180°5. 根据电视台天气预报:某市明天降雨的概率为80%,对此信息,下列几种说法中正确的是( )
A、∠1=∠3 B、∠2=∠5 C、∠2+∠4=180° D、∠2+∠3=180°5. 根据电视台天气预报:某市明天降雨的概率为80%,对此信息,下列几种说法中正确的是( )
A、该市明天一定会下雨 B、该市明天有80%地区会降雨 C、该市明天有80%的时间会降雨 D、该市明天下雨的可能性很大6. 用一块含角的透明直角三角板画已知的边BC上的高,下列三角板的摆放位置正确的是( )A、 B、
B、 C、
C、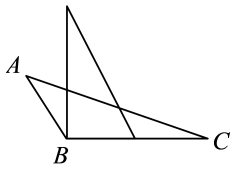 D、
D、 7. 若三角形的两边长分别为3和8,则下列长度的四条线段中能作为第三边的是( )A、3 B、5 C、8 D、128. 一个角的余角比这个角大 , 则这个角的度数为( )A、 B、 C、 D、9. 如图,向高为H的圆柱形空水杯中注水,表示注水量y与水深x的关系的图象是下面哪一个?( )
7. 若三角形的两边长分别为3和8,则下列长度的四条线段中能作为第三边的是( )A、3 B、5 C、8 D、128. 一个角的余角比这个角大 , 则这个角的度数为( )A、 B、 C、 D、9. 如图,向高为H的圆柱形空水杯中注水,表示注水量y与水深x的关系的图象是下面哪一个?( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图所示分割正方形,各图形面积之间的关系验证了一个等式,这个等式是( )
10. 如图所示分割正方形,各图形面积之间的关系验证了一个等式,这个等式是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
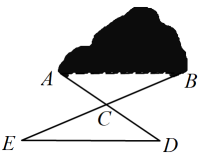
11. 计算:;12. 如图,有一座小山,现要在小山A,B的两端开一条隧道,施工队要知道A,B两端的距离,于是先在平地上取一个可以直接到达点A和点B的点C,连接并延长到D,使 , 连接并延长到E,使 , 连接 . 经测量 , , 的长度分别为 , , , 则A,B之间的距离为m;
 13. 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=25°,则∠EAC的度数= .
13. 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=25°,则∠EAC的度数= . 14. 如图,在中, , 利用尺规在 , 上分别截取;分别以点M,N为圆心,以大于的长为半径作弧,两弧在内部交于点E;作射线交于点F.若 , 点H为线段上的一动点,则的最小值是 .
14. 如图,在中, , 利用尺规在 , 上分别截取;分别以点M,N为圆心,以大于的长为半径作弧,两弧在内部交于点E;作射线交于点F.若 , 点H为线段上的一动点,则的最小值是 . 15. 任意给一个非零数m,按下列程序进行计算,则输出结果为;
15. 任意给一个非零数m,按下列程序进行计算,则输出结果为; 16. 已知MN是线段AB的垂直平分线,P、Q是直线MN上两点,且∠PAB=35°,∠QBA=60°,则∠QAP的度数为 .
16. 已知MN是线段AB的垂直平分线,P、Q是直线MN上两点,且∠PAB=35°,∠QBA=60°,则∠QAP的度数为 .三、解答题
-
17. 计算:(1)、 .(2)、(用简便方法计算).18. 先化简,再求值: , 其中 , .19. 如图,现有一个转盘被平均分成6等份,分别标有数字2,3,4,5,6,7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字,
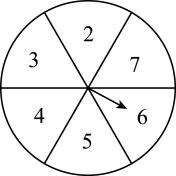 (1)、转到数字10是(从“随机事件”“必然事件”“不可能事件”中选一个填入);(2)、转动转盘,转出的数字是2的倍数比转出的数字是3的倍数的可能性(从“大”“小”“相等”中选一个填入);(3)、转动转盘,转出的数字大于3的概率是;(4)、现有一张写有数字5的卡片,要随机转动转盘,转盘停止后记下转出的数字,与卡片上的数字和为奇数的概率是 .20. 如图, , .
(1)、转到数字10是(从“随机事件”“必然事件”“不可能事件”中选一个填入);(2)、转动转盘,转出的数字是2的倍数比转出的数字是3的倍数的可能性(从“大”“小”“相等”中选一个填入);(3)、转动转盘,转出的数字大于3的概率是;(4)、现有一张写有数字5的卡片,要随机转动转盘,转盘停止后记下转出的数字,与卡片上的数字和为奇数的概率是 .20. 如图, , . (1)、请按要求填空并说明;
(1)、请按要求填空并说明;解:因为 ,
所以 , (根据: )
又因为 ,
所以▲ ,
所以 ,
∴(根据: );
(2)、若平分 , 于点 , , 请直接写出的度数.21. 如图,在正方形网格中,的三个顶点均在格点上. (1)、画出 , 使得和关于直线对称;(2)、过点C作线段 , 使得 , 且 .22. 如图,正方形的边长为a,点E在边上,四边形也是正方形,它的边长为b(),连接 , , .
(1)、画出 , 使得和关于直线对称;(2)、过点C作线段 , 使得 , 且 .22. 如图,正方形的边长为a,点E在边上,四边形也是正方形,它的边长为b(),连接 , , . (1)、用含a,b的代数式表示的长;(2)、若 , , 用含x的代数式表示两个正方形的面积和;(3)、若 , 的面积为K,求出K的值.23. 晚上7点15分,小李骑自行车从家出发到距离家3500米远的水上公园看7点40分开始的水上灯光秀,如图所示是小李从家到公园路途中离家的距离与离家时间之间的关系.
(1)、用含a,b的代数式表示的长;(2)、若 , , 用含x的代数式表示两个正方形的面积和;(3)、若 , 的面积为K,求出K的值.23. 晚上7点15分,小李骑自行车从家出发到距离家3500米远的水上公园看7点40分开始的水上灯光秀,如图所示是小李从家到公园路途中离家的距离与离家时间之间的关系.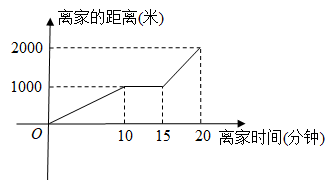 (1)、在这个变化过程中,自变量、因变量分别是什么?(2)、观察图象分析,出发后10分到15分之间可能发生了什么情况?(3)、求这一段骑行中的最高速度是多少?(4)、如果继续按照(3)中的最高速度骑行,小李能否在灯光秀开始时赶到公园?为什么?24. 第一学习小组按照老师留的预习任务,对如下问题进行了自主探究性学习:
(1)、在这个变化过程中,自变量、因变量分别是什么?(2)、观察图象分析,出发后10分到15分之间可能发生了什么情况?(3)、求这一段骑行中的最高速度是多少?(4)、如果继续按照(3)中的最高速度骑行,小李能否在灯光秀开始时赶到公园?为什么?24. 第一学习小组按照老师留的预习任务,对如下问题进行了自主探究性学习:已知:如图1所示,在中, , , 是的中线,过点C作 , 垂足为M,且交于点E.
 (1)、【探究一:相等的角】
(1)、【探究一:相等的角】同学们用量角器度量后猜想 , 请你先判断他们的猜想是否符合题意,再用所学知识说明理由;
(2)、【探究二:相等的线段】如图2所示,组员小亮在(1)的条件上添加了一条线段 , 且平分交于点N,即可得 , 并给出了说明理由;请你和他共同完成下面的说理过程.
解:如图2中,
因为平分 , ,
所以 , (依据: )
因为 ,
所以 ,
所以 ,
在和中,
因为▲ , ▲ , ▲
所以(依据: ),
所以 . (依据: )
(3)、【探究三:全等的三角形】如图3所示,组员小刚在(2)的条件上,连接 , 又发现了一组全等三角形,请直接写出这组全等三角形.
25. 已知:如图所示,在中, , , , 垂足为E,过点A作交延长线于点D.点P在线段上,且 , 点M在线段上,且 , 延长交于点Q,连接 . (1)、【观察分析】填空:
(1)、【观察分析】填空:的度数是;的度数是;的度数是;
(2)、【猜想说理】判断与的数量关系,并说明理由;(3)、【拓展延伸】若点P关于的对称点N恰好落在的延长线上,若 , , , 请根据题意补全图形,并直接写出线段的长及的度数.