辽宁省丹东市东港市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
1. 某种微生物长度约为0.0000035米,将0.0000035用科学记数法表示为( )A、 B、 C、 D、2. 如图是由边长为1的小正方形组成的网格,若在这个网格面上随意抛一粒豆子,则豆子落在阴影区域的概率为( )
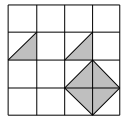 A、 B、 C、 D、3. 如图,直线a∥b,直线c与直线a,b分别交于点A,B,AD⊥b于点D,若∠1=57°,则∠2的度数为( )
A、 B、 C、 D、3. 如图,直线a∥b,直线c与直线a,b分别交于点A,B,AD⊥b于点D,若∠1=57°,则∠2的度数为( )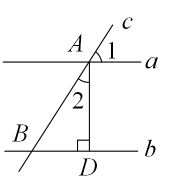 A、30° B、32° C、33° D、40°4. 如图,的两条角平分线 , 交于点P,若 , 则为( )
A、30° B、32° C、33° D、40°4. 如图,的两条角平分线 , 交于点P,若 , 则为( ) A、112° B、115° C、120° D、125°5. 计算的结果是( ).A、 B、3 C、 D、6. 如图,在△ABC中,∠C=90°,∠1=∠2,BC=16cm,点D到AB的距离为6cm,则BD的长为( )
A、112° B、115° C、120° D、125°5. 计算的结果是( ).A、 B、3 C、 D、6. 如图,在△ABC中,∠C=90°,∠1=∠2,BC=16cm,点D到AB的距离为6cm,则BD的长为( )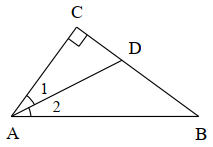 A、 B、 C、 D、7. 已知 , 则b的值为( )A、4 B、 C、12 D、8. 如图,若 , , , 则的度数是( )
A、 B、 C、 D、7. 已知 , 则b的值为( )A、4 B、 C、12 D、8. 如图,若 , , , 则的度数是( )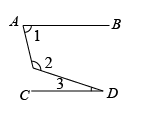 A、25° B、30° C、36° D、38°
A、25° B、30° C、36° D、38°二、填空题
-
9. 计算 .10. 圆柱的底面半径为 , 设圆柱的体积为V,圆柱的高为 , 则V与h的关系式是 , 当h每增加时,V会增加 .11. 如图, , 与互补,当 , 时,的度数为 .
 12. 等腰三角形的一个角是50°,则它的顶角的度数是 .13. 若 , 则 .14. 如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,若∠B=70°,∠C=40°,则∠DAE的度数为 .
12. 等腰三角形的一个角是50°,则它的顶角的度数是 .13. 若 , 则 .14. 如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,若∠B=70°,∠C=40°,则∠DAE的度数为 . 15. 如图,在△ABC中,DF,EM分别垂直平分边AB,AC,若△AFM的周长为9,则BC= .
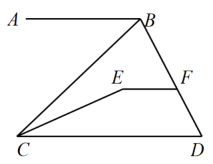
15. 如图,在△ABC中,DF,EM分别垂直平分边AB,AC,若△AFM的周长为9,则BC= .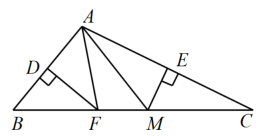 16. 如图,桌面上放置一个等腰直角△ABC,直角顶点C顶着桌面,若另外两个顶点与桌面的距离分别为和 , 过另外两个顶点向桌面作垂线,则两个垂足之间的距离DE的长度为 .
16. 如图,桌面上放置一个等腰直角△ABC,直角顶点C顶着桌面,若另外两个顶点与桌面的距离分别为和 , 过另外两个顶点向桌面作垂线,则两个垂足之间的距离DE的长度为 .
三、解答题
-
17. 要求:利用乘法公式计算(1)、(2)、18. 先化简,再求值:
, 其中 , .
19. 如图,有一钝角 , 在边上有一点C.请用尺规作图在内找到一点P,使点P到 , 的距离相等;并且点P到点O,点C的距离也相等(要求:尺规作图,不写作法,保留作图痕迹). 20. 现有一个均匀的正方体,六个面上分别标有1,2,3,4,5,5.(1)、任意掷出这个正方体,朝上的数字是1的概率是;(2)、任意掷出这个正方体,朝上的数字大于4的概率是;(3)、甲、乙二人用这个正方体做游戏,规定掷这个正方体一次,朝上数字是偶数则甲获胜,否则乙获胜.请你判断甲和乙谁获胜的概率大,并简要说明理由.21. 完成下面的说理过程:(不用抄题,直接将所填内容写到答题卡上即可)
20. 现有一个均匀的正方体,六个面上分别标有1,2,3,4,5,5.(1)、任意掷出这个正方体,朝上的数字是1的概率是;(2)、任意掷出这个正方体,朝上的数字大于4的概率是;(3)、甲、乙二人用这个正方体做游戏,规定掷这个正方体一次,朝上数字是偶数则甲获胜,否则乙获胜.请你判断甲和乙谁获胜的概率大,并简要说明理由.21. 完成下面的说理过程:(不用抄题,直接将所填内容写到答题卡上即可)已知:如图,点E在线段的延长线上,点F在线段的延长线上,连接E, , , .
求证: .

证明:因为( ▲ ),
又因为(已知),
所以(等量代换),
所以(同旁内角互补,两直线平行),
所以( ▲ ),
因为(已知),
所以(等量代换),
所以( ▲ ),
所以( ▲ ).
22. 周末早晨,小明父子两人同时从家出发跑步锻炼身体.小明跑步速度快,跑了一段时间后立即以一定的速度按原路返回,与爸爸相遇后,父子两人按小明返回时的速度返回家中.下面的图象反映的是父子两人离家的距离和离家的时间的关系,观察图象回答问题: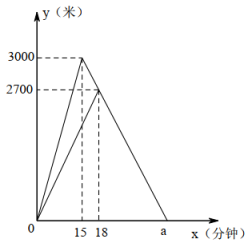 (1)、小明去广场时的速度是米/分;
(1)、小明去广场时的速度是米/分;爸爸去广场时的速度是米/分;
父子两返回时的速度是米/分;
(2)、a表示的数字是;(3)、直接写出运动过程中父子两人何时相距200米.

