辽宁省大连市高新园区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
1. 4 的算术平方根是( )A、2 B、±2 C、16 D、±162. 在 , 0,1,这组数中,最小的数是( ).A、 B、 C、0 D、13. 在平面直角坐标系中,下列各点在第三象限的是( )A、 B、 C、 D、4. 下列调查中,适合采用“普查”方式的是( ).A、调查某品牌手机市场占有率 B、调查大连市市民实施低碳生活的情况 C、调查你所在班级的同学的身高 D、调查某型号LED灯的使用寿命5. 如图,直线AB∥CD,∠EFB=60°,则∠CGE的度数是( )
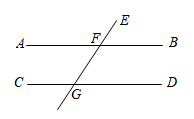 A、130° B、110° C、120° D、60°6. 不等式的解集在数轴上的表示,正确的是( )A、
A、130° B、110° C、120° D、60°6. 不等式的解集在数轴上的表示,正确的是( )A、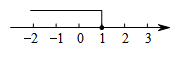 B、
B、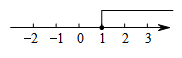 C、
C、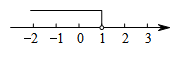 D、
D、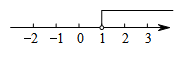 7. 已知是方程的一个解,那么a的值是( )A、 B、 C、9 D、108. 已知实数a、b,若 , 则下列结论中,不成立的是( ).A、 B、 C、 D、9. 某玩具厂共有300名生产工人,每个工人每天可生产玩具车架20个或车轮40个,且1个车架与4个车轮可配成一套,设有x个工人生产车架,y个工人生产车轮,下列方程组正确的是( )A、 B、 C、 D、10. 平面直角坐标系中,点 , , 经过点A的直线轴,点C是直线a上的一个动点,当线段BC的长度最短时,点C的坐标为( ).A、 B、 C、 D、
7. 已知是方程的一个解,那么a的值是( )A、 B、 C、9 D、108. 已知实数a、b,若 , 则下列结论中,不成立的是( ).A、 B、 C、 D、9. 某玩具厂共有300名生产工人,每个工人每天可生产玩具车架20个或车轮40个,且1个车架与4个车轮可配成一套,设有x个工人生产车架,y个工人生产车轮,下列方程组正确的是( )A、 B、 C、 D、10. 平面直角坐标系中,点 , , 经过点A的直线轴,点C是直线a上的一个动点,当线段BC的长度最短时,点C的坐标为( ).A、 B、 C、 D、二、填空题
-
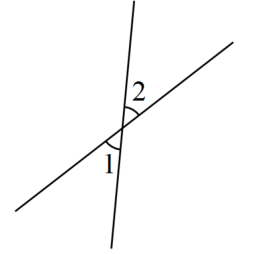
11. 不等式的解集是 .12. 如图,与是对顶角, , , 则°.
 13. 若0,则 .14. 《九章算术》是我国古代一部著名的算书,它的出现标志着中国古代数学形成了完整的体系.其中卷八方程[七]中记载:“今有牛五、羊二,直金八两.牛二、羊五,直金六两.牛、羊各一只直金几何?”题目大意是:5头牛、2只羊共值金8两.2头牛、5只羊共值金6两.1头牛和1只羊值金两.15. 若是关于x的不等式的一个解,则a的取值范围是 .16. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点 , ……那么点的坐标为 .
13. 若0,则 .14. 《九章算术》是我国古代一部著名的算书,它的出现标志着中国古代数学形成了完整的体系.其中卷八方程[七]中记载:“今有牛五、羊二,直金八两.牛二、羊五,直金六两.牛、羊各一只直金几何?”题目大意是:5头牛、2只羊共值金8两.2头牛、5只羊共值金6两.1头牛和1只羊值金两.15. 若是关于x的不等式的一个解,则a的取值范围是 .16. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点 , ……那么点的坐标为 .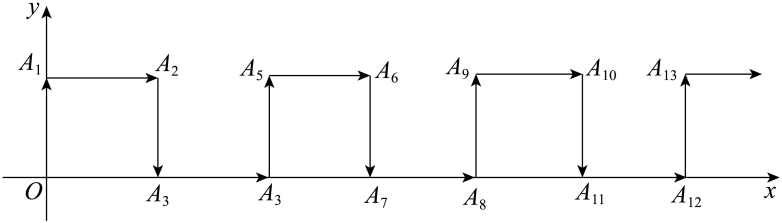
三、解答题
-
17. 解不等式组 , 并把解集在数轴上表示出来.18. 某中学组织了“国家安全知识竞赛”,现从中随机抽取部分学生的成绩作为样本,按“优秀”、“良好”、“合格”、“不合格”四个等级进行统计,绘制了如下尚不完整的统计图表.
测试成绩统计表
等级
频数(人数)
频率
优秀
36
a
良好
b
0.4
合格
0.2
不合格
c
合计
1
测试成绩条形统计图

根据统计图表提供的信息,解答下列问题:
(1)、a= , b= , c=;(2)、若该校有800名学生参加了本次测试,估计测试成绩等级在良好以上(包括良好)的学生约有多少人?19. 如图,直线AB,CD相交于点O, . (1)、若 , 求的度数;(2)、如果 , 那么ON与CD互相垂直吗?请说明理由.20. 如图,在平面直角坐标系中,已知A(-1,4),B(-2,1).C(-4,1),将三角形ABC向右平移3个单位再向下平移2个单位得到三角形A1B1C1 , 点A、B、C的对应点分别是点A1、B1、C1 .
(1)、若 , 求的度数;(2)、如果 , 那么ON与CD互相垂直吗?请说明理由.20. 如图,在平面直角坐标系中,已知A(-1,4),B(-2,1).C(-4,1),将三角形ABC向右平移3个单位再向下平移2个单位得到三角形A1B1C1 , 点A、B、C的对应点分别是点A1、B1、C1 .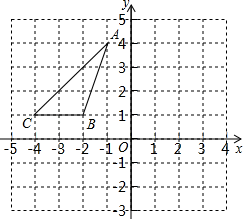 (1)、画出三角形A1B1C1 , 并直接写出点A1、B1、C1的坐标;(2)、直接写出三角形A1B1C1的面积;(3)、点M(2a-b,b)在线段BC上.其平称后的对应点为M1(a+b.a),求点M的坐标.21. 阅读下列材料:
(1)、画出三角形A1B1C1 , 并直接写出点A1、B1、C1的坐标;(2)、直接写出三角形A1B1C1的面积;(3)、点M(2a-b,b)在线段BC上.其平称后的对应点为M1(a+b.a),求点M的坐标.21. 阅读下列材料:∵ , 即 . ∴的整数部分为1,小数部分为 .
请根据材料提示,进行解答:
(1)、的整数部分是 , 小数部分是;(2)、若的小数部分为a,的整数部分为b,求的值;(3)、若的整数部分为2,求m的取值范围.22. 为了更好的做好疫情防控工作,区教育局准备为辖区内中小学及幼儿园购买一批立式红外线测温仪.已知购买3个A品牌测温仪和2个B品牌测温仪共需310元,购买2个A品牌测温仪和1个B品牌测温仪共需180元.(1)、求A、B两种品牌的立式红外线测温仪销售单价各是多少元?(2)、区教育局决定购进A、B两种品牌测温仪共50个.恰逢生产厂家对两种品牌测温仪的售价进行调整.A品牌测温仪售价提高了10%,B品牌测温仪按九折出售.如果区教育局准备购买A、B两种品牌测温仪的总费用不超过3250元,则至少购买A品牌测温仪多少个?(3)、在(2)的条件下,如果购买A品牌的测温仪不超过23个.求怎样购买总费用最低?最低费用多少元?23. 如图1,点E、F分别在直线AB、CD上,点P为AB、CD之间的一点,且 .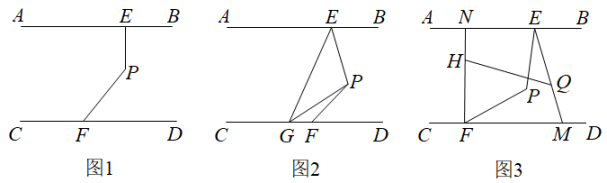 (1)、求证:;(2)、如图2,点G在射线FC上,PG平分 , , 探究与之间的数量关系.并说明理由;(3)、如图3, , . 直线HQ分别交FN,EM于H、Q两点,若 , 求的度数.24. 在平面直角坐标系中,点 , 点 , 点B在点A的右侧,过点A作轴于C,连接AB,BC,三角形ABC的面积为6.(1)、求m的值;(2)、点D在线段CB的延长线上,且横坐标为8,连接AD,求的度数;(3)、线段AB以每秒1个单位的速度向右水平移动t秒,A,B的对应点分别为M,N.过点作x轴的垂线与线段MN交于点Q,三角形PQM的面积记为 , 三角形PQN的面积记为 , 若 , 求t的取值范围.
(1)、求证:;(2)、如图2,点G在射线FC上,PG平分 , , 探究与之间的数量关系.并说明理由;(3)、如图3, , . 直线HQ分别交FN,EM于H、Q两点,若 , 求的度数.24. 在平面直角坐标系中,点 , 点 , 点B在点A的右侧,过点A作轴于C,连接AB,BC,三角形ABC的面积为6.(1)、求m的值;(2)、点D在线段CB的延长线上,且横坐标为8,连接AD,求的度数;(3)、线段AB以每秒1个单位的速度向右水平移动t秒,A,B的对应点分别为M,N.过点作x轴的垂线与线段MN交于点Q,三角形PQM的面积记为 , 三角形PQN的面积记为 , 若 , 求t的取值范围.