辽宁省朝阳市建平县2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
1. 下列四个图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、x2+x2=x4 B、(a-b)2=a2-b2 C、(-a2)3=-a6 D、3a2·2a3=6a63. 经研究发现,2019年新型冠状病毒,它的单细胞的直径范围在60纳米~140纳米(1纳米=10﹣9米)之间,则最大直径140纳米用科学记数法表示为( )A、140×10﹣9米 B、14×10﹣8米 C、1.4×10﹣7米 D、1.4×107米4. 下列说法正确的是( )A、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 B、等腰三角形的高、中线、角平分线互相重合 C、“长度为3cm,4cm,5cm的三条线段可以构成三角形”是必然事件 D、“400人中有两人生日在同一天”是随机事件5. 如图,下列各组条件中,不能得到的是( )
2. 下列运算正确的是( )A、x2+x2=x4 B、(a-b)2=a2-b2 C、(-a2)3=-a6 D、3a2·2a3=6a63. 经研究发现,2019年新型冠状病毒,它的单细胞的直径范围在60纳米~140纳米(1纳米=10﹣9米)之间,则最大直径140纳米用科学记数法表示为( )A、140×10﹣9米 B、14×10﹣8米 C、1.4×10﹣7米 D、1.4×107米4. 下列说法正确的是( )A、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 B、等腰三角形的高、中线、角平分线互相重合 C、“长度为3cm,4cm,5cm的三条线段可以构成三角形”是必然事件 D、“400人中有两人生日在同一天”是随机事件5. 如图,下列各组条件中,不能得到的是( ) A、 , B、 , C、 , D、 ,6. 如图,将△ABC沿过边上两点D,E的直线折叠后,使得点B与点A重合,若已知BE=4cm,则△ABC的周长与△ADC的周长的差为( )
A、 , B、 , C、 , D、 ,6. 如图,将△ABC沿过边上两点D,E的直线折叠后,使得点B与点A重合,若已知BE=4cm,则△ABC的周长与△ADC的周长的差为( ) A、4cm B、5cm C、8cm D、10cm7. 如图,一只小狗在如图所示的方砖上走来走去,最终停留在阴影方砖上的概率是( )
A、4cm B、5cm C、8cm D、10cm7. 如图,一只小狗在如图所示的方砖上走来走去,最终停留在阴影方砖上的概率是( ) A、 B、 C、 D、8. 如图所示、有三种卡片,其中边长为a的正方形卡片有1张,长为a,宽为b的矩形卡片有4张,边长为b的正方形卡片有4张,用这9张卡片刚好供成一个大正方形,则这个大正方形的边长为( )
A、 B、 C、 D、8. 如图所示、有三种卡片,其中边长为a的正方形卡片有1张,长为a,宽为b的矩形卡片有4张,边长为b的正方形卡片有4张,用这9张卡片刚好供成一个大正方形,则这个大正方形的边长为( ) A、a+2b B、2a+2b C、2a+b D、a+b9. 某校八年级同学到距学校6千米的郊外秋游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,L1L2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数关系,则以下判断错误的是( )
A、a+2b B、2a+2b C、2a+b D、a+b9. 某校八年级同学到距学校6千米的郊外秋游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,L1L2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数关系,则以下判断错误的是( ) A、骑车的同学比步行的同学晚出发30分钟 B、骑车的同学和步行的同学同时到达目的地 C、骑车的同学从出发到追上步行的同学用了20分钟 D、步行的速度是6千米/小时.10. 如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设点P经过的路程为x,以A,P,B为顶点的三角形面积为y,则下列图象能大致反映y与x的函数关系的是( )
A、骑车的同学比步行的同学晚出发30分钟 B、骑车的同学和步行的同学同时到达目的地 C、骑车的同学从出发到追上步行的同学用了20分钟 D、步行的速度是6千米/小时.10. 如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设点P经过的路程为x,以A,P,B为顶点的三角形面积为y,则下列图象能大致反映y与x的函数关系的是( ) A、
A、 B、
B、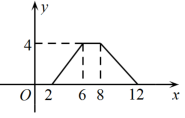 C、
C、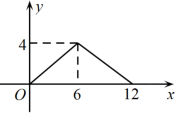 D、
D、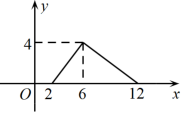
二、填空题
-
11. 已知:am=2,an=3,则a2m+n= .12. 若m2+n2=5,m+n=3,则mn= .13. 等腰三角形的一条边长为4cm,另一条边长为6cm,则它的周长是 .14. 已知 , , , 则a,b,c的大小关系为 .15. 如图,在中, , M是AB的中点,交AC于点N,的周长是7cm,则BC的长为 .
 16. 三角形的两边长分别为2cm,5cm,第三边的长xcm也是整数,则当三角形的周长取最大值时,x的值是 .
16. 三角形的两边长分别为2cm,5cm,第三边的长xcm也是整数,则当三角形的周长取最大值时,x的值是 .三、解答题
-
17. 计算:(1)、(﹣2a2b)3+8(a2)2•(﹣a)2•(﹣b)3;(2)、(x﹣3)0﹣()﹣2+(﹣1)2021+|﹣5|.18. 先化简,再求值: , 其中 .19. 请将下列证明过程补充完整.
已知:如图,已知∠1+∠2=180°,∠3=∠8.求证:∠AEO=∠ACB.

证明:∵∠1+∠4=180°(平角定义),
∠1+∠2=180°(已知),
∴∠2=∠4(同角的补角相等).
∴DB∥EF( ).
∴∠3+ ▲ =∠180°( ).
又∵∠3=∠B(已知),
∴∠B+=180°(等量代换).
∴▲∥▲(同旁内角互补,两直线平行).
∴∠AED=∠ACB( ).
20. 一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球的个数是白球个数的2倍少5个,已知从袋中摸出一个球是红球的概率是.(1)、求袋中红球的个数;(2)、求从袋中摸出一个球是白球的概率;(3)、取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.21. 如图描述了一辆汽车在某一直路上的行驶过程,汽车离出发地的路程s(km)和行驶时间t(h)之间的关系,请根据图象回答问题: (1)、汽车共行驶的路程是多少千米?(2)、汽车在行驶途中停留了多长时间?(3)、汽车从行驶途中停留到汽车到达离出发地最远的地方行驶的路程是多少千米?(4)、汽车到达离出发地最远的地方后返回,则返回用了多长时间?(5)、汽车在返回时的平均速度是多少?22. 尺规作图,不写作法,保留作图痕迹
(1)、汽车共行驶的路程是多少千米?(2)、汽车在行驶途中停留了多长时间?(3)、汽车从行驶途中停留到汽车到达离出发地最远的地方行驶的路程是多少千米?(4)、汽车到达离出发地最远的地方后返回,则返回用了多长时间?(5)、汽车在返回时的平均速度是多少?22. 尺规作图,不写作法,保留作图痕迹已知:线段a和∠α
求作:△ABC,使得AB=a , BC=2a , ∠ABC=∠α.
 23. 如图,在△ABC中,AD为∠BAC的角平分线,FE垂直平分AD,垂足为E,EF交BC的延长线于点F,若∠CAF=50°,求∠B的度数.
23. 如图,在△ABC中,AD为∠BAC的角平分线,FE垂直平分AD,垂足为E,EF交BC的延长线于点F,若∠CAF=50°,求∠B的度数.

