江西省宜春市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
1. 算术平方根等于3的是( )A、 B、3 C、9 D、2. 在平面直角坐标系中,将线段AB平移后得到线段 ,点 的对应点 的坐标为 ,则点 的对应点 的坐标为( )A、 B、 C、 D、3. 点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=3cm,则点P到直线l的距离为( )A、4cm B、5cm C、小于3cm D、不大于3cm4.
如图所示,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,则∠BOF为( )
 A、35° B、30° C、25° D、20°5. 下列调查中最适合采用全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某校七年级1班50名同学的视力情况 C、端午节期间,食品安全检查部门调查市场上粽子的质量情况 D、调查某池塘中现有鱼的数量6. 如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长度,P1 , P2 , P3 , ……均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,﹣1),P5(﹣1,﹣1),P6(﹣1,2)……,根据这个规律,点P2022的坐标为( )
A、35° B、30° C、25° D、20°5. 下列调查中最适合采用全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某校七年级1班50名同学的视力情况 C、端午节期间,食品安全检查部门调查市场上粽子的质量情况 D、调查某池塘中现有鱼的数量6. 如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长度,P1 , P2 , P3 , ……均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,﹣1),P5(﹣1,﹣1),P6(﹣1,2)……,根据这个规律,点P2022的坐标为( ) A、(﹣505,﹣505) B、(505,﹣506) C、(505,505) D、(﹣505,506)
A、(﹣505,﹣505) B、(505,﹣506) C、(505,505) D、(﹣505,506)二、填空题
-
7. 把“对顶角相等”改写成“如果…那么…”的形式 .8. 已知点 在第二象限,且到 轴的距离是 ,到 轴的距离是3,则点 的坐标为9. 《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十,问甲、乙持钱各几何?”译文:“假设有甲乙二人,不知其钱包里有多少钱,若乙把自己一半的钱给甲,则甲的钱数为50;而甲把自己 的钱给乙,则乙的钱数也能为50.问甲、乙各有多少钱?”设甲持钱数为x,乙持钱数为y,可列方程组为 .10. 如图, , 直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2= .
 11. 若 , 则= .12. 若整数a使关于x的不等式组 , 有且只有45个整数解,则a的值为 .
11. 若 , 则= .12. 若整数a使关于x的不等式组 , 有且只有45个整数解,则a的值为 .三、解答题
-
13.(1)、计算:;(2)、解不等式 .14. 按要求完成下列证明:
如图,E点为DF上的点,B为AC上的点, , , 试说明: .
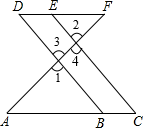
证明:
∵(已知),( ),
∴(等量代换).
∴▲( ).
∴( ).
又(已知),
∴(等量代换).
∴( ).
15. 如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,△ABC的三个顶点均在格点上.
( 1 )将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A'B'C',画出平移后△A'B'C';
( 2 )建立适当的平面直角坐标系,使得点A的坐为(﹣4,3);
( 3 )在(2)的条件下,直接写出点B'的坐标.
16. 有大小两种货车,2辆大车与3辆小车一次共可运货16吨,5辆大车与6辆小车一次共可运货37吨,求1辆大车与1辆小车一次共可运货多少吨?17. 如图,∠1=∠ABC,∠2=∠3,FG⊥AC于F,判断BE与AC有怎样的位置关系,并说明理由. 18. 某校为了加强学生的安全意识,组织学生参加安全知识竞赛,并从中抽取了部分学生的成绩进行统计,绘制了两幅尚不完整的统计图如图所示,根据统计图中的信息,解答下列问题:
18. 某校为了加强学生的安全意识,组织学生参加安全知识竞赛,并从中抽取了部分学生的成绩进行统计,绘制了两幅尚不完整的统计图如图所示,根据统计图中的信息,解答下列问题: (1)、频数分布直方图中a=;(2)、扇形统计图中n= ▲ , 并补全频数分布直方图;(3)、若成绩在80分以上为优秀,全校共有1500名学生,请估计成绩优秀的学生有多少名?19. 如图所示,在平面直角坐标系中,点A,B的坐标分别为 , , 且a,b满足 , 点C的坐标为 .
(1)、频数分布直方图中a=;(2)、扇形统计图中n= ▲ , 并补全频数分布直方图;(3)、若成绩在80分以上为优秀,全校共有1500名学生,请估计成绩优秀的学生有多少名?19. 如图所示,在平面直角坐标系中,点A,B的坐标分别为 , , 且a,b满足 , 点C的坐标为 .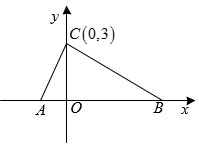 (1)、求a,b的值及;(2)、若点M在x轴上,且 , 试求点M的坐标.20. 阅读下面的材料:
(1)、求a,b的值及;(2)、若点M在x轴上,且 , 试求点M的坐标.20. 阅读下面的材料:对于实数 ,我们定义符号 的意义为:当 时, ;当 时, ,如: .
根据上面的材料回答下列问题:
(1)、 ;(2)、当 时,求x的取值范围.21. 问题:已知线段AB∥CD,在AB、CD间取一点P(点P不在直线AC上),连接PA、PC,试探索∠APC与∠A、∠C之间的关系. (1)、端点A、C同向:
(1)、端点A、C同向:如图1,点P在直线AC右侧时,∠APC﹣(∠A+∠C)=度;
如图2,点P在直线AC左侧时,∠APC+(∠A+∠C)=度;
(2)、端点A、C反向:如图3,点P在直线AC右侧时,∠APC与∠A﹣∠C有怎样的等量关系?写出结论并证明;
如图4,点P在直线AC左侧时,∠APC﹣(∠A﹣∠C)= ▲ 度.