江西省吉安市遂川县2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-09-07 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $m \times {(- m)}^{2}$ 所得结果为（　　）

A、 $- m^{2}$ B、 $m^{2}$ C、 $- m^{3}$ D、 $m^{3}$

查看试题解析
2. 下列是北京大学，中国科学院，中国医科大学和中国人民公安大学的标志中的图案，其中是轴对称图形的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如图所示，在所标识的角中，内错角是（　　）

A、 $∠ 1$ 和 $∠ 2$ B、 $∠ 2$ 和 $∠ 3$ C、 $∠ 2$ 和 $∠ 4$ D、 $∠ 1$ 和 $∠ 3$

查看试题解析
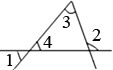4. 下列不能用平方差公式计算的是（　　）

A、 $(x + y) (x - y)$ B、 $(- x + y) (x - y)$ C、 $(- x + y) (- x - y)$ D、 $(- x + y) (x + y)$

查看试题解析
5. 如图，某市夏天的温度随时间变化的图象，通过观察可知，下列说法中错误的是（　　）

A、这天15时温度最高 B、这天3时温度最低 C、这天最高温度与最低温度的差是 $13 ° C$ D、这天0～3时，15～24时温度在下降

查看试题解析
6. 如图1，将1个长方形沿虚线剪开得到两个长方形，再将这两个长方形拼成图2，则下列等式可以解释两图形面积变化的数量关系的是（　　）

A、 $(x + 3) (x - 2) = x (x + 1) - 6$ B、 ${(x + 3)}^{2} = x (x + 6) + 9$ C、 $(x - 3) (x - 2) = x (x - 5) + 6$ D、 $(x + 3) (x - 3) = x^{2} - 9$

查看试题解析

二、填空题

7. 若 $∠ 1$ 与 $∠ 2$ 互为邻补角，且 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为．

查看试题解析
8. 甲型 $H 1 N 1$ 流感在墨西哥爆发并在全球蔓延，研究表明，甲型 $H 1 N 1$ 流感球型病毒细胞的直径约为 $0.00000156 m$ ，用科学记数法表示这个数是m．

查看试题解析
9. 如图，三角形ABC的高AD=4，BC=6，点E在BC上运动，若设BE的长为 $x ，$ 三角形ACE的面积为有y，则y与x的关系式为.

查看试题解析
10. 一副直角三角板如图放置，点D在边 $B C$ 上，点F在 $A B$ 的延长线上， $A F / / D E ， ∠ A = ∠ D F E = 90 °$ ，则 $∠ F D B$ 的余角的度数为度．

查看试题解析
11. 若 $x + y = 4$ ， $x y = 1$ ，则 $x^{2} + y^{2} - 2 =$ ．

查看试题解析
12. 如图，一幅三角板的两个直角顶点重合，已知 $∠ B = 30 °$ ， $∠ C = 45 °$ ，则当 $△ A O B$ 的一边与 $△ C O D$ 的一边平行或重合，且点C在 $O A$ 的左侧时， $∠ C O B$ （小于平角）的度数为．

查看试题解析

三、解答题

13.

(1)、计算： ${(- 2 a^{3} b^{2})}^{3} \div 8 a^{2} b^{6}$ ；

(2)、如图所示， $O A ⊥ O B$ ， $O C ⊥ O D$ ， $∠ B O D$ 比 $∠ A O C$ 大 $100 °$ ，求 $∠ A O D$ 的度数．

查看试题解析
14. 为了有效提高人民免疫水平，最终阻断病毒传染，某地接种新冠疫苗，已知每天可接种800人．

(1)、直接写出接种人数y与时间x（天）之间的函数关系式；

(2)、如果计划接种6.4万人，则需要多天才能完成接种任务？

查看试题解析
15. 先化简，再求值： ${2b}^{2} + (a+b) (a - b) - {(a - b)}^{2}$ ，其中a=﹣3，b= $\frac{1}{2}$ ．

查看试题解析
16. 一不透明的布袋里，装有红、黄、蓝三种颜色的小球（除颜色外其余都相同），其中有红球2个，蓝球1个，黄球若干个，现从中任意摸出1个球是红球的概率为 $\frac{1}{2}$ ．

(1)、求口袋中黄球的个数；

(2)、现规定：摸到红球得5分，摸到黄球得3分，摸到蓝球得2分（每次摸后放回），乙同学在一次摸球游戏中，第一次随机摸到一个红球第二次又随机摸到一个蓝球，若随机再摸一次，求乙同学三次摸球所得分数之和不低于10分的概率．

查看试题解析
17. 如图，在所标注的角中．

(1)、对顶角有对，邻补角有对；

(2)、若 $∠ 2 + ∠ 3 = 70 °$ ， $∠ 1 = 150 °$ ，求 $∠ 3$ 与 $∠ 4$ 的度数．

查看试题解析

18. 某公交车每月的支出费用为4000元，每月的乘车人数x(人)与每月利润(利润＝收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的)：

x(人)	500	1000	1500	2000	2500	3000	…
y(元)	﹣3000	﹣2000	﹣1000	0	1000	2000	…

(1)、在这个变化过程中，是自变量，是因变量；

(2)、观察表中数据可知，每月乘客量达到人以上时，该公交车才不会亏损；

(3)、请你估计当每月乘车人数为3500人时，每月利润为多少元？

查看试题解析

19. 把推理过程补充完整，并填写相应的理由．
如图，∵AC∥EF（已知），
∴ $∠ 1 = ∠ 2$ ．（        ）
$∠ B E F = ∠ A$ ．（        ）
又∵ $E F$ 平分 $∠ B E D$ （已知），
∴ $∠ 2 =$       ▲       ．（        ）
∴ $∠ 1 = ∠ A$ ．（        ）

查看试题解析
20.
如图，A、B两点分别位于一个池塘的两侧，池塘西边有一座假山D，在DB的中点C处有一个雕塑，小川从点A出发，沿直线AC一直向前经过点C走到点E，并使CE＝CA，然后他测量点E到假山D的距离，则DE的长度就是A、B两点之间的距离．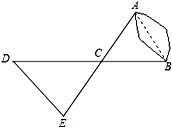

(1)、你能说明小川这样做的根据吗？

(2)、如果小川恰好未带测量工具，但是知道A和假山D、雕塑C分别相距200米、120米，你能帮助他确定AB的长度范围吗？

查看试题解析
21. 如图，将两个长方形用不同方式拼成图1和图2两个图形．

(1)、若图1中的阴影部分面积为 $a^{2} - b^{2}$ ，则图2中的阴影部分面积为（用含字母a，b的代数式表示）；

(2)、由（1）你可以得到的等式是；

(3)、根据你所得到的等式解决下面的问题：
①若 $x^{2} - y^{2} = 16$ ， $x - y = 2$ ，则 $x + y =$ ；

②计算： $67.7 5^{2} - 32.2 5^{2}$ ．

查看试题解析
22. 观察下列运算过程：
$2^{2} = 2 \times 2 = 4$ ， ${(\frac{1}{2})}^{- 2} = \frac{1}{{(\frac{1}{2})}^{2}} = \frac{\frac{1}{1}}{\frac{1}{4}} = 4$ ； ${(\frac{3}{4})}^{2} = \frac{3}{4} \times \frac{3}{4} = {(\frac{4}{3})}^{- 2} = \frac{1}{{(\frac{4}{3})}^{2}} = \frac{1}{\frac{4}{3} \times \frac{4}{3}} = \frac{3}{4} \times \frac{3}{4}$ ， …

(1)、根据以上运算过程和结果，我们发现： $2^{2} =$ ； ${(\frac{3}{4})}^{2} =$ ；

(2)、仿照（1）中的规律，判断 ${(\frac{3}{2})}^{3}$ 与 ${(\frac{2}{3})}^{- 3}$ 的大小关系；

(3)、求 ${(- \frac{3}{8})}^{- 4} \times {(\frac{3}{4})}^{4} \div {(\frac{1}{2})}^{- 3}$ 的值．

查看试题解析
23. 如图，在 $△$ ABC中，∠ACB＝90°，AC＝BC，AB＝8cm，过点C作射线CD，且CD∥AB，点P从点C出发，沿射线CD方向匀速运动，速度为3cm/s；点Q从点A出发，沿AB边向点B匀速运动，速度为1cm/s，当点Q停止运动时，点P也停止运动．连接PQ，CQ，设动点的运动时间为t（s）（0＜t＜8），解答下列问题：

(1)、用含有t的代数式表示CP和BQ的长度；

(2)、当t＝2时，请说明PQ∥BC；

(3)、设 $△ B C Q$ 的面积为S（cm²），求S与t之间的关系式．

查看试题解析