江西省赣州市寻乌县2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
1. 下列各点中,在第一象限内的点是( )A、 B、 C、 D、2. 下列调查方式中,最合适的是( )A、为了解某品牌灯泡的使用寿命,采用全面调查的方式 B、为了解我市居民的节水意识,采用全面调查的方式 C、对一枚用于发射卫星的运载火箭各部件的检查,采用抽样调查的方式 D、为了解我市八年级学生对在线学习课程的满意度情况,采用抽样调查的方式3. 下列说法不一定成立的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则4. 如图,已知直线 , 点B在直线a上,点A,C在直线b上,且 . 若 , 则∠2的度数是( )
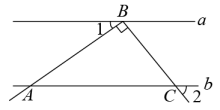 A、45° B、50° C、55° D、60°5. 已知 , 则的值为( )A、1 B、2 C、3 D、96. 如图,直线 , 相交于点O, , , 平分 , 给出下列结论:①当时,;②为的平分线;③若时,;④ . 其中正确的结论有( )
A、45° B、50° C、55° D、60°5. 已知 , 则的值为( )A、1 B、2 C、3 D、96. 如图,直线 , 相交于点O, , , 平分 , 给出下列结论:①当时,;②为的平分线;③若时,;④ . 其中正确的结论有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
7. 比较大小: (填“ ”、“ ”、“ ”).8. 不等式的解集是 .9. 如图,已知直线AB,CD被EF所截,EG是∠AEF的角平分线,若∠1=∠2,∠2+∠4=120°,则∠3=°.
 10. 已知直线过点 , 且与轴平行,直线过点 , 并与轴平行,则两直线的交点坐标是 .11. 如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1 , O2 , O3 , …组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2021秒时,点P的坐标是 .
10. 已知直线过点 , 且与轴平行,直线过点 , 并与轴平行,则两直线的交点坐标是 .11. 如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1 , O2 , O3 , …组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2021秒时,点P的坐标是 . 12. 将长为4宽为a(a大于1且小于4)的长方形纸片按如图所示的方式折叠并压平,剪下一个边长等于长方形宽的正方形,称为第一次操作;再把剩下的长方形按同样的方式操作,称为第二次操作;如此反复操作下去 ,若在第n次操作后,剩下的长方形恰为正方形,则操作终止.当 时,a的值为.
12. 将长为4宽为a(a大于1且小于4)的长方形纸片按如图所示的方式折叠并压平,剪下一个边长等于长方形宽的正方形,称为第一次操作;再把剩下的长方形按同样的方式操作,称为第二次操作;如此反复操作下去 ,若在第n次操作后,剩下的长方形恰为正方形,则操作终止.当 时,a的值为.
三、解答题
-
13.(1)、计算:;(2)、解方程组: .14. 解不等式组并写出它的解集在数轴上表示出来.
 15. 已知 的立方根是 , 的算术平方根是 , 是 的整数部分,求 的平方根.16. 如图,A(-1,0),C(1,4)点B在x轴上,且AB=3.
15. 已知 的立方根是 , 的算术平方根是 , 是 的整数部分,求 的平方根.16. 如图,A(-1,0),C(1,4)点B在x轴上,且AB=3. (1)、求点B的坐标,并画出△ABC;(2)、求△ABC的面积.17. 如图,已知 , . 求证: .
(1)、求点B的坐标,并画出△ABC;(2)、求△ABC的面积.17. 如图,已知 , . 求证: . 18. 针对春节期间新型冠状病毒事件,九(1)班学生参加学校举行的“珍惜生命.远离病毒”知识竞赛初赛,赛后班长对成绩进行分析,制作如下的频数分布表、频数分布直方图和扇形统计图(未完成).
18. 针对春节期间新型冠状病毒事件,九(1)班学生参加学校举行的“珍惜生命.远离病毒”知识竞赛初赛,赛后班长对成绩进行分析,制作如下的频数分布表、频数分布直方图和扇形统计图(未完成).类别
分数段
频数(人数)
A
60≤x<70
a
B
70≤x<80
16
C
80≤x<90
24
D
90≤x<100
6

请根据以上统计图表解答下列问题:
(1)、该班总人数为;(2)、频数分布表中a=;(3)、扇形统计图中,类别B所在扇形的圆心角是 .(4)、全校共有720名学生参加初赛,估计该校成绩“D”(90≤x<100范围内)的学生有多少人?19. 规定min(m,n)表示m,n中较小的数(m,n均为实数,且mn),例如:min{3,﹣1}=﹣1,、min 据此解决下列问题:(1)、min =;(2)、若min =2,求x的取值范围;(3)、若min{2x﹣5,x+3}=﹣2,求x的值.20. 如图,在每个小正方形边长均为1个单位长度的方格中,有一个且的每个顶点均与小正方形的顶点重合 (1)、在方格中,将向下平移5个单位长度得到 , 请画出 .(2)、求平移到的过程中,所扫过的面积.21. 已知关于x的不等式组(1)、当时,求该不等式组的整数解;(2)、若原不等式组的整数解只有7,8,求m的取值范围.22. 潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
(1)、在方格中,将向下平移5个单位长度得到 , 请画出 .(2)、求平移到的过程中,所扫过的面积.21. 已知关于x的不等式组(1)、当时,求该不等式组的整数解;(2)、若原不等式组的整数解只有7,8,求m的取值范围.22. 潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:种植户
种植A类蔬菜面积
(单位:亩)
种植B类蔬菜面积
(单位:亩)
总收入
(单位:元)
甲
3
1
12500
乙
2
3
16500
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)、求A、B两类蔬菜每亩平均收入各是多少元?(2)、某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.23. 如图,在平面直角坐标系中,已知 , , 且满足 , 是的算术平方根,将线段平移至 , 点D在x轴正半轴上(不与点A重合),连接 , , , . (1)、直接写出点A、B、C的坐标;(2)、当的面积是的面积的3倍时,求点D的坐标;(3)、已知 , 设 , , , 判断、、之间的数量关系,并说明理由.
(1)、直接写出点A、B、C的坐标;(2)、当的面积是的面积的3倍时,求点D的坐标;(3)、已知 , 设 , , , 判断、、之间的数量关系,并说明理由.