江西省赣州市石城县2021-2022学年七年级下学期期末考数学试题

试卷更新日期：2022-09-07 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数 $- 1$ ， $- \sqrt{2}$ ， $0$ ， $\frac{1}{4}$ 中，最小的实数是（）

A、 $- \sqrt{2}$ B、 $- 1$ C、 $0$ D、 $\frac{1}{4}$

查看试题解析
2. 已知a<b，下列式子不一定成立的是（）

A、a-1<b-1 B、-2a>-2b C、2a+1<2b+1 D、ma<mb

查看试题解析
3. 要反映花都区六月上旬每天的最高气温的变化趋势，最宜采用（）

A、折线图 B、条形图 C、扇形图 D、直方图

查看试题解析
4. 如图，下列条件中，不能判定 $A B ∥ C D$ 的是（）

A、 $∠ D + ∠ B A D = 180 °$ B、 $∠ 1 = ∠ 2$ C、 $∠ 3 = ∠ 4$ D、 $∠ B = ∠ D C E$

查看试题解析
5. 如图，将周长为8的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长是（　　）

A、8 B、10 C、12 D、16

查看试题解析
6. 平面直角坐标系中，对于点P(x，y)，我们把点P(-y+1，x+1)叫做点P“伴随点”已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ， …，这样依次得到点A₁ ， A₂ ， A₃ ， …，An，…若点A₁的坐标为(2，4)，点A₂₀₂₂的坐标为（）

A、(-3，3) B、(-2，-2) C、(3，-1) D、(2，4)

查看试题解析

二、填空题

7. 如图，取两根木条a、b，将它们钉在一起并把它们想象成两条直线，就得到一个相交线模型，测量发现∠1=∠2，其数学原理是．

查看试题解析
8. 若a、b为实数，且满足 $| a - 2 | + \sqrt{3 - b} = 0$ ，则 $b - a$ 的值为．

查看试题解析
9. 已知平面直角坐标系中点A（1，b-2）在第四象限上，则b的取值范围是．

查看试题解析
10. 已知x、y满足方程组 ${\begin{array}{l} 2 x + y = 6 \\ x + 2 y = - 3 \end{array}$ 的解，则x+y= ．

查看试题解析
11. 如图，直线AB、CD相交于点O，OE丄AB于O， ∠DOE=35°，则∠AOC= ．

查看试题解析
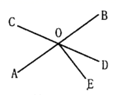12. 在平面直角坐标系中，有点A（2，4），点B（0，2），若在坐标轴上有一点C（不与点B重合），使三角形AOC和三角形AOB面积相等，则点C的坐标为．

查看试题解析

三、解答题

13.

(1)、计算： $\sqrt[3]{- 8} + \sqrt{(- 2)^{2}} + \sqrt{12}$ ；

(2)、解方程组： ${\begin{array}{l} x - y = 1 \\ 3 x + y = 7 \end{array}$ ．

查看试题解析
14. 已知某正数的两个平方根分别是a＋3和2a－15，b的立方根是－2，求3a＋b的算术平方根．

查看试题解析
15. 解不等式组 ${\begin{array}{l} \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1 \\ 5 x - 1 < 3 (x + 1) \end{array}$ ，并在数轴上表示不等式组的解集．

查看试题解析
16. 完成下列证明过程，并在括号内填上依据．
如图，点E在 $A B$ 上，点 $F$ 在 $C D$ 上， $∠ 1 = ∠ 2$ ， $∠ B = ∠ C$ ．求证：AB $/ /$ CD．
证明： $∵ ∠ 1 = ∠ 2$ （已知）， $∠ 1 = ∠ 4$ （），
$∴ ∠ 2 =$       ▲      （等量代换），
$∴$       ▲       $/ / B F ($ 同位角相等，两直线平行 $)$ ，
$∴ ∠ 3 = ∠$ C（　                                                                                                            　）．
又 $∵ ∠ B = ∠ C$ （已知），
$∴ ∠ 3 = ∠ B$ （　                                                　），
$∴ A B / / C D$ （　                                                                                                                                          　）．

查看试题解析
17. 如图，在直角坐标系中，已知A（﹣1，4），B（﹣2，1），C（﹣4，1），将 $△ A B C$ 向右平移3个单位再向下平移2个单位得到 $△ A_{1} B_{1} C_{1}$ ，点A、B、C的对应点分别是点A₁、B₁、C₁ ．

(1)、画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、直接写出点A₁、B₁、C₁的坐标；

(3)、直接写出 $△ A_{1} B_{1} C_{1}$ 的面积．

查看试题解析
18. 茜茜受《乌鸦喝水》故事的启发，利用量筒、大球和小球进行了如下操作，请根据图中给出的信息，解答下列问题：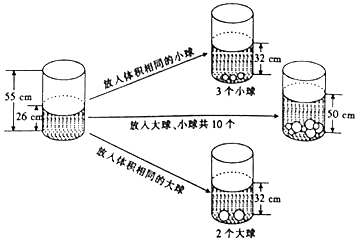

(1)、放入一个小球水面升高cm，放入一个大球水面升高cm.

(2)、如果要使水面上升到50cm，应放入大球、小球各多少个？

查看试题解析
19. 如图，已知AB∥CD．直线EF分别交直线AB、CD于点E、F，∠EFB=∠B，FH⊥FB．

(1)、求证：FH平分∠GFD．

(2)、若∠B=20°，求∠DFH的度数；

查看试题解析
20. 某学校想了解学生家长对“双减”政策的认知情况，随机抽查了部分学生家长进行调查，将抽查的数据结果进行统计，并绘制两幅不完整的统计图（A：不太了解，B：基本了解，C：比较了解，D：非常了解）.请你根据图中提供的信息回答以下问题：

(1)、请求出这次被调查的学生家长共有多少人？

(2)、请补全条形统计图.

(3)、试求出扇形统计图中“比较了解”部分所对应的圆心角度数.

(4)、该学校共有1200名学生家长，估计对“双减”政策了解程度为“非常了解”的学生家长大约有多少？

查看试题解析
21. 为进一步推进我县中小学教育信息化工程，某校计划增添一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元．

(1)、求每台电脑、每台电子白板各多少万元？

(2)、根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，该校至多购进电脑多少台？

查看试题解析
22. 在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S=ah.例如：三点坐标分别为A（1，2），B（-3，1），C（2，-2），则“水平底”a=5，“铅垂高”h=4，“矩面积”S=ah=20.根据所给定义解决下列问题：

(1)、若已知点D（1，2）、E（-2，1）、F（0，6），则这3点的“矩面积”=.

(2)、若D（1，2）、E（-2，1）、F（0，t）三点的“矩面积”为18，求点F的坐标；

查看试题解析
23. 已知：如图，直线 $P Q ∥ M N$ ，点C是PQ，MN之间（不在直线PQ，MN上）的一个动点.

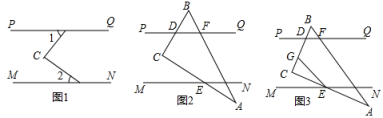(1)、若∠1与∠2都是锐角，如图1，请直接写出∠C与∠1∠2之间的数量关系.

(2)、若小明把一块三角板（∠A=30°，∠C=90°）如图2放置，点D，E，F是三角板的边与平行线的交点，若∠AEN=∠A，求∠BDF的度数.

(3)、将图2中的三角板进行适当转动，如图3，直角顶点C始终在两条平行线之间，点G在线段CD上，连结EG，且有∠CEG=∠CEM，给出下列两个结论：
① $\frac{∠ G E N}{∠ B D F}$ 的值不变；
②∠GEN－∠BDF的值不变.
其中只有一个是正确的，你认为哪个是正确的？讲求出不变的值是多少.

查看试题解析