江西省赣州市南康区2021-2022学年七年级下学期期末检测数学试题

试卷更新日期：2022-09-07 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，已知点P(5，−5)，则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列说法中正确的是（）

A、4的算术平方根是2 B、64的平方根是8 C、16的立方根是±4 D、﹣64没有立方根

查看试题解析
3. 已知点A(a，100)与点B(101，b)关于y轴对称，则a+b的值（）

A、1 B、﹣1 C、201 D、﹣201

查看试题解析
4. 《九章算术》是中国传统数学的重要著作，方程术是它的最高成就．其中记载：今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？译文：今有人合伙购物，每人出 $8$ 钱，会多 $3$ 钱；每人出 $7$ 钱，又会差 $4$ 钱，问人数、物价各是多少？设合伙人数为 $x$ 人，物价为 $y$ 钱，以下列出的方程组正确的是（）

A、 ${\begin{matrix} y - 8 x = 3 \\ y - 7 x = 4 \end{matrix}$ B、 ${\begin{matrix} y - 8 x = 3 \\ 7 x - y = 4 \end{matrix}$ C、 ${\begin{matrix} 8 x - y = 3 \\ y - 7 x = 4 \end{matrix}$ D、 ${\begin{matrix} 8 x - y = 3 \\ 7 x - y = 4 \end{matrix}$

查看试题解析
5. 为了调查疫情对青少年人生观、价值观产生的影响，某学校团委对初二级部学生进行了问卷调查，其中一项是：疫情期间出现的哪一个高频词汇最触动你的内心？针对该项调查结果制作的两个统计图（不完整）如下，由图中信息可知，下列结论错误的是（）

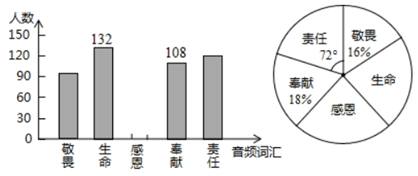A、本次调查的样本容量是 $600$ B、选“责任”的有 $120$ 人 C、扇形统计图中“生命”所对应的扇形圆心角度数为 ${64.8}^{\circ}$ D、选“感恩”的人数最多

查看试题解析
6. 如图，已知直线AB，CD被直线AC所截， $A B ∥ C D$ ， E是平面内任意一点（点E不在直线AB，CD，AC上），设∠BAE＝α，∠DCE＝β，下列各式：①β﹣α，②α﹣β，③180°﹣α+β，④360°﹣α﹣β，可以表示∠AEC的度数的有（）

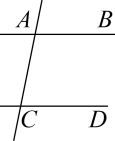A、③④ B、①③④ C、①②④ D、②③④

查看试题解析

二、填空题

7. 计算： $\sqrt[3]{27} =$ ．

查看试题解析
8. 点P(3，﹣2)向下平移2个单位得到点Q，则点Q的坐标是．

查看试题解析
9. 语句“x的2倍与5的和大于4”用不等式表示为．

查看试题解析
10. 如图，AB∥CD，AD⊥AC，∠BAD＝35°，则∠ACD＝°．

查看试题解析
11. 在数据学习的实践活动中，小明对本班40名学生的血型作了统计，并列出了下列统计表，根据统计表可计算本班血型为O型的学生有人．
组别
A型
B型
AB型
O型
频率
0.4
0.35
0.1
n

查看试题解析
12. 在平面直角坐标系中，有点A（2，4），点B（0，2），若在坐标轴上有一点C（不与点B重合），使三角形AOC和三角形AOB面积相等，则点C的坐标为．

查看试题解析

三、解答题

13. 计算： $(- 1)^{2022} + | \sqrt{2} - 2 | - \sqrt{9}$ ．

查看试题解析
14. 解方程组： ${\begin{array}{l} x - 2 y = 2 ① \\ 3 x + 2 y = 6 ② \end{array}$ ．

查看试题解析
15. 请把以下推理过程填写完整：
已知：如图，∠1＝∠2，∠3+∠4＝180°，求证：a $∥$ c．
证明：∵∠1＝∠2（已知），
∴▲       $∥$       ▲（　内错角相等，两直线平行　）．
∵∠3+∠4＝180°（已知），
∴b $∥$ c（       ）．
∴a $∥$ c（       ）．

查看试题解析
16. x取哪些整数值时，不等式 $5 x - 2 > 3 (x - 1)$ 和 $\frac{1}{2} x - 1 ≤ 3 - \frac{3}{2} x$ 都成立？请通过计算进行说明．

查看试题解析
17. 如图，在7×12的方格纸中，每个小正方形的边长为一个长度单位，点A、B、C都在格点上．

(1)、将线段BC向上平移2个单位得到线段DE，在方格纸中画出线段DE，连接AD，AE；

(2)、三角形ADE的面积＝．

查看试题解析
18. 为了解某校七年级学生身高情况，随机测量了m位同学的身高（单位：cm），并根据测得的数据绘制了两幅不完整的统计图（A.150~155，B.155~160，C.160~165，D.165~170，E.170~175），请结合图中提供的信息，解答下列问题：

(1)、m= ， C所在扇形的圆心角度数是°；

(2)、补全频数分布直方图；

(3)、若该校七年级计划开展大课间体操比赛，要求每班应安排不低于本班人数30%的学生参加，并希望参赛学生的身高差距较小，请问你觉得应安排哪个范围的学生参赛更合适，并说说你的理由．

查看试题解析
19. 已知关于x，y的二元一次方程组 ${\begin{array}{l} x + y = 6 \\ 2 x - y = 3 k \end{array}$ 的解为 ${\begin{array}{l} x = m \\ y = n \end{array}$ ．

(1)、求m，n的值（用含k的代数式表示）；

(2)、若点(m，n)在第四象限，求k的取值范围．

查看试题解析
20. 计算下列各式的值：

(1)、 $\sqrt{2} (\sqrt{2} + 2)$ ；

(2)、 $\sqrt{3} (\sqrt{3} + \frac{1}{\sqrt{3}})$ ．

查看试题解析
21. 有理数a、b、c在数轴上的位置如图．

(1)、用“＞”或“＜”填空：b﹣c0，a+b+30， $\sqrt{2} + b + c$ 0．

(2)、化简： $| \sqrt{2} + b + c | - | a + b + 3 | - | a - c + \sqrt{2} |$ ．

查看试题解析
22. 有大、小两种货车，2辆大车与3辆小车一次可以运货15.5吨；5辆大车与6辆小车一次可以运货35吨．求3辆大车与5辆小车一次可以运货多少吨？

查看试题解析
23. 为进一步提升摩托车、电动自行车骑乘人员和汽车驾乘人员安全防护水平，公安部交通管理局部署在全国开展“一盔一带”安全守护行动．某商店销售A，B两种头盔，进价和售价如表所示，请根据表格信息下列问题．
名称
A种头盔
B种头盔
进价（元/个）
60
40
售价（元/个）
80
50

(1)、该商店购进A，B两种头盔共100个，用去4600元钱，求A，B两种头盔各购进了多少个？

(2)、经过几天销售后商店发现销量较好，于是又用5400元钱购进这两种头盔若干个，要想将这两次购进的头盔售完后所获总利润不低于3000元，则该商店第二次至少应购进A种头盔多少个？

查看试题解析
24. 如图，点 $D$ ， $E$ ， $F$ 分别是三角形 $A B C$ 的边 $B C$ ， $C A$ ， $A B$ 上的点， $D E / / B A$ ， $D F / / C A$ ．求证： $∠ A = ∠ E D F$ ．

查看试题解析
25. 已知AB∥CD，点E在射线BC上，连接AE，DE，设∠BAE＝α，∠CDE＝β．

(1)、如图1，当点E在线段BC上时，∠AED＝（用含α，β的式子表示）；

(2)、如图2，当点E在线段BC的延长线上时．
①判断∠AED与α，β的数量关系，并说明理由；
②若M为平面内一动点，且MA∥ED，请直接写出∠MAB与β的数量关系．

查看试题解析

名称	A种头盔	B种头盔
进价（元/个）	60	40
售价（元/个）	80	50

组别	A型	B型	AB型	O型
频率	0.4	0.35	0.1	n