吉林省松原市乾安县2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
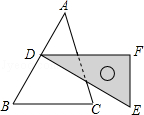
1. 下列计算正确的是( )A、 =±15 B、 =﹣3 C、= D、2. 已知a<b,则下列式子正确的是( )A、a+5>b+5 B、3a>3b C、﹣5a>﹣5b D、3. 若点P是第二象限内的点,且点P到x轴的距离是2,到y轴的距离是3,则点P的坐标是 ( )A、(2,3) B、(2,-3) C、(-3,2) D、(3,-2)4. 下列调查最适合于抽样调查的是( )A、某校要对七年级学生的身高进行调查 B、卖早餐的师傅想了解一锅茶鸡蛋的咸度 C、班主任了解每位学生的家庭情况 D、了解九年级一班全体学生立定跳远的成绩5. 如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB.若∠B为锐角,BC∥DF,则∠B的大小为( )
 A、30° B、45° C、60° D、75°6. 若方程3m(x+1)+1=m(3-x)-5x的解是负数,则m的取值范围是( ) .A、m>-1.25 B、m<-1.25 C、m>1.25 D、m<1.25
A、30° B、45° C、60° D、75°6. 若方程3m(x+1)+1=m(3-x)-5x的解是负数,则m的取值范围是( ) .A、m>-1.25 B、m<-1.25 C、m>1.25 D、m<1.25二、填空题
-
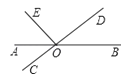
7. 把“对顶角相等”改写成“如果…那么…”的形式 .8. 已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为.9. 平方根节是数学爱好者的节日,这一天的月份和日期的数字正好是当年年份最后两位数字的平方根,例如2009年的3月3日。请你写出本世纪内你喜欢的一个平方根节(题中所举例子除外):年月日.10. 不等式2x+1>3x-2的非负整数解是.11. 在实数①﹣ , ② , ③0.3,④ , ⑤ , ⑥ , ⑦0.373737773…(每相邻两个3之间依次多一个7)中,属于无理数的有 .12. 如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC,则∠BOD=
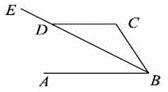
 13. 已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、6,第五组的频率是0.2,那么第六组的频数是 .14. 一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=.
13. 已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、6,第五组的频率是0.2,那么第六组的频数是 .14. 一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=.
三、解答题
-
15. 计算: .16. 解方程组: .17. 解不等式组: , 并在数轴上表示不等式的解集.18. 如图,AB∥CD,BE平分∠ABC,∠DCB=140°,求∠ABD和∠EDC的度数.
 19. 如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
19. 如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,
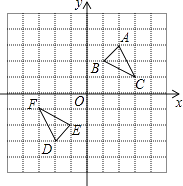
解答下列问题:
(1)、分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;(2)、若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.(3)、求图中△ABC的面积.20.(1)、计算:
= , = , = , = , = ,
根据计算结果,回答:一定等于a吗?你发现其中的规律了吗?请你用自己的语言描述出来.(2)、利用你总结的规律,计算: .21. 已知关于 , 的方程组 的解满足不等式组 ,求满足条件的 的整数值.22. 为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.组别
捐款额(x)元
户数
A
1≤x<50
a
B
50≤x<100
10
C
100≤x<150
D
150≤x<200
E
x≥200
请结合以上信息解答下列问题.
 (1)、a= , 本次调查样本的容量是;
(1)、a= , 本次调查样本的容量是;
(2)、补全“捐款户数分组统计表和捐款户数统计图1”;
(3)、若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?
23. 如图,已知AB∥CD,EF∥MN,∠1=115°, (1)、求∠2和∠4的度数;(2)、本题隐含着一个规律,请你根据(1)的结果进行归纳:如果一个角的两边分别平行于另一个角的两边,那么这两个角;(3)、利用(2)的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的两倍,求这两个角的大小.24. 已知x,y满足方程组且x+y<0.(1)、试用含m的式子表示方程组的解;(2)、求实数m的取值范围;(3)、化简|m+|-|2-m|.25. 销售有限公司到某汽车制造有限公司选购A、B两种型号的轿车,用300万元可购进A型轿车10辆,B型轿车15辆;用300万元可购进A型轿车8辆,B型轿车18辆.(1)、求A、B两种型号的轿车每辆分别多少元?(2)、若该汽车销售公司销售一辆A型轿车可获利8000元,销售一辆B型轿车可获利5000元,该汽车销售公司准备用不超过400万元购进A、B两种型号轿车共30辆,且这两种轿车全部售出后总获利不低于20.4万元,问:有几种购车方案?在这几种购车方案中,哪种获利最多?26. 如图1,在平面直角坐标系中,点A,B的坐标分别为A(m,0),B(n,0)且m、n满足|m+2|+=0,现同时将点A,B分别向上平移3个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)、求∠2和∠4的度数;(2)、本题隐含着一个规律,请你根据(1)的结果进行归纳:如果一个角的两边分别平行于另一个角的两边,那么这两个角;(3)、利用(2)的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的两倍,求这两个角的大小.24. 已知x,y满足方程组且x+y<0.(1)、试用含m的式子表示方程组的解;(2)、求实数m的取值范围;(3)、化简|m+|-|2-m|.25. 销售有限公司到某汽车制造有限公司选购A、B两种型号的轿车,用300万元可购进A型轿车10辆,B型轿车15辆;用300万元可购进A型轿车8辆,B型轿车18辆.(1)、求A、B两种型号的轿车每辆分别多少元?(2)、若该汽车销售公司销售一辆A型轿车可获利8000元,销售一辆B型轿车可获利5000元,该汽车销售公司准备用不超过400万元购进A、B两种型号轿车共30辆,且这两种轿车全部售出后总获利不低于20.4万元,问:有几种购车方案?在这几种购车方案中,哪种获利最多?26. 如图1,在平面直角坐标系中,点A,B的坐标分别为A(m,0),B(n,0)且m、n满足|m+2|+=0,现同时将点A,B分别向上平移3个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.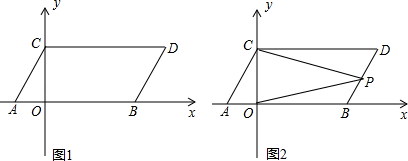 (1)、求点C,D的坐标;(2)、求四边形OBDC的面积;(3)、如图2,点P是线段BD上的一个动点,连接PC、PO,当点P在线段BD上移动时(不与B,D重合)的值是否发生变化,并说明理由.
(1)、求点C,D的坐标;(2)、求四边形OBDC的面积;(3)、如图2,点P是线段BD上的一个动点,连接PC、PO,当点P在线段BD上移动时(不与B,D重合)的值是否发生变化,并说明理由.