吉林省白城市大安市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
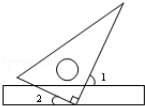
1. 在平面直角坐标系中,点(-3,4)所在的象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列实数是无理数的是( )A、-2 B、 C、 D、3. 下列调查中,适宜采用全面调查(普查)方式的是( )A、对我市市民实施低碳生活情况的调查 B、对我国首架大型民用飞机零部件的检查 C、对全国中学生心理健康现状的调查 D、对市场上的冰淇淋质量的调查4. 不等式2x﹣1>3的解集( )A、x>1 B、x>﹣2 C、x>2 D、x<25. 如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
 A、10° B、15° C、20° D、25°6. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹 两,牛每头 两,根据题意可列方程组为( )A、 B、 C、 D、
A、10° B、15° C、20° D、25°6. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹 两,牛每头 两,根据题意可列方程组为( )A、 B、 C、 D、二、填空题
-
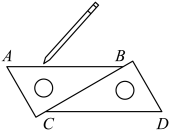
7. 一次数学测试后,某班50名学生的成绩被分为5组,第1~4组的频数分别为12、10、15、8,则第5组的频率是.8. 把方程写成用含的代数式表示的形式,则 .9. 若是关于x,y的二元一次方程3x+ay=5的一个解,则a的值为10. 如图,小明在两块按如图所示的方式摆放的含30°角的直角三角板的边缘画直线AB、CD,得到 , 这是根据 , 两直线平行.
 11. AB∥CD , ∠1=58°,FG平分∠EFD , 则∠FGB的度数为 .
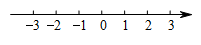
11. AB∥CD , ∠1=58°,FG平分∠EFD , 则∠FGB的度数为 .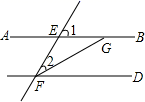 12. 若a<<b,且a,b为连续正整数,则b-a=13. 将点B (-3, 2)先向右平移m个单位长度,再向上平移n个单位后得到点B.(-1,5),则mn的值为14. 如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点 , , , , ,…,则 的坐标是.
12. 若a<<b,且a,b为连续正整数,则b-a=13. 将点B (-3, 2)先向右平移m个单位长度,再向上平移n个单位后得到点B.(-1,5),则mn的值为14. 如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点 , , , , ,…,则 的坐标是.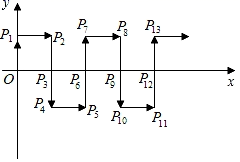
三、解答题
-
15. 计算: - + 1.16. 解方程组17. 解不等式:3x﹣1>2(x﹣1),并把它的解集在数轴上表示出来.
 18. 如图,在△ABC中,点D、E分别在AB、BC 上,且 , ∠1=∠2.求证: ;
18. 如图,在△ABC中,点D、E分别在AB、BC 上,且 , ∠1=∠2.求证: ;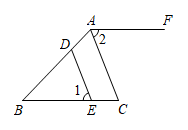 19. 如图,先将△ABC向左平移3个单位长度,然后再向下平移4个单位长度,得到△A1B1C1
19. 如图,先将△ABC向左平移3个单位长度,然后再向下平移4个单位长度,得到△A1B1C1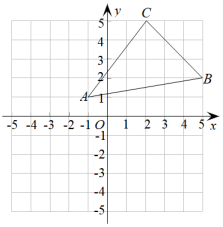 (1)、画出经过两次平移后的图形,并写出A1、B1、C1的坐标;(2)、求ΔABC的面积.20. 甲,乙两人合作加工一批三条腿和四条腿两种型号的凳子(如图所示).加工完后,甲说:“我做了40条凳子腿”,乙说:“我做了12个凳子面”,求三条腿凳子和四条腿凳子各有多少个.
(1)、画出经过两次平移后的图形,并写出A1、B1、C1的坐标;(2)、求ΔABC的面积.20. 甲,乙两人合作加工一批三条腿和四条腿两种型号的凳子(如图所示).加工完后,甲说:“我做了40条凳子腿”,乙说:“我做了12个凳子面”,求三条腿凳子和四条腿凳子各有多少个.
 21. 疫情期间,线上推出的“腾讯会议”软件已成为同学们学习的得力助手,为了解同学们对该软件使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如图所示的两幅尚不完整的统计图.
21. 疫情期间,线上推出的“腾讯会议”软件已成为同学们学习的得力助手,为了解同学们对该软件使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如图所示的两幅尚不完整的统计图.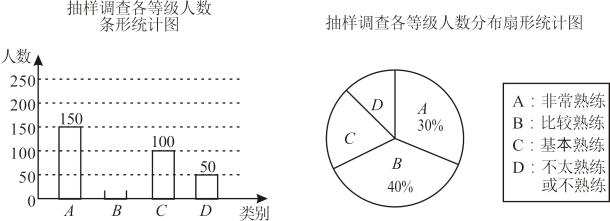
根据以上信息,回答下列问题:
(1)、本次调查的样本容量是 , 扇形统计图中表示B等级的扇形圆心角为;(2)、补全条形统计图;(3)、学校拟对“不太熟练或不熟练”的同学进行平台使用的培训,若该校有2000名学生,试估计该校需要培训的学生人数.22. 如图AF 与BD相交于点C,∠B=∠ACB, 且CD平分∠ECF.求证: .请完成下列推理过程:
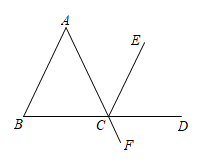
证明:∵CD 平分∠ECF
∴∠ECD= ▲ ( )
∵∠ACB=∠FCD( )
∴∠ECD=∠ACB( )
∵∠B=∠ACB
∴∠B=∠▲( )
∴ ( ).
23. 在解方程组 时,由于粗心,甲看错了方程组中的a,得到的解为 ,乙看错了方程组中的b,得到的解为 .(1)、求正确的a,b的值;(2)、求原方程组的解.24. 如图: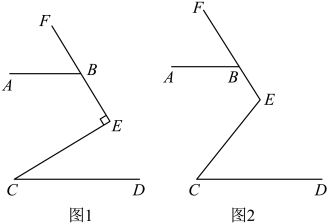 (1)、如图1,∠CEF=90°,点B在射线EF上,若∠ABF=50°,∠C=40° ,试判断AB、CD的位置关系,并说明理由;(2)、如图2,∠CEF=120° ,点B在射线EF上,且 . 则∠ABE与∠C的数量关系为:25. 疫情过后,某中学为学生复课做准备,计划购买消毒水和洗手液两种物品。若购买8瓶消毒水和5瓶洗手液需用220元;若购买4瓶消毒水和6瓶洗手液需用152元.(1)、求每瓶消毒水和每瓶洗手液各多少元.(2)、学校决定购买消毒水和洗手液共75瓶,总费用不超过1180元,那么最多可以购买多少瓶消毒水?26. 如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a, 0),点C的坐标为(0,b),且a、b满足+|b- 12|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的路线移动.
(1)、如图1,∠CEF=90°,点B在射线EF上,若∠ABF=50°,∠C=40° ,试判断AB、CD的位置关系,并说明理由;(2)、如图2,∠CEF=120° ,点B在射线EF上,且 . 则∠ABE与∠C的数量关系为:25. 疫情过后,某中学为学生复课做准备,计划购买消毒水和洗手液两种物品。若购买8瓶消毒水和5瓶洗手液需用220元;若购买4瓶消毒水和6瓶洗手液需用152元.(1)、求每瓶消毒水和每瓶洗手液各多少元.(2)、学校决定购买消毒水和洗手液共75瓶,总费用不超过1180元,那么最多可以购买多少瓶消毒水?26. 如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a, 0),点C的坐标为(0,b),且a、b满足+|b- 12|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的路线移动.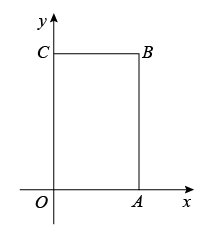 (1)、点B的坐标为;当点 P移动5秒时,点P的坐标为(2)、在移动过程中,当点P移动11秒时,求△OPB的面积.(3)、在(2)的条件下,坐标轴上是否存在点Q,使△OPQ与△OPB的面积相等.若存在,直接写出点Q的坐标;若不存在,请说明理由.
(1)、点B的坐标为;当点 P移动5秒时,点P的坐标为(2)、在移动过程中,当点P移动11秒时,求△OPB的面积.(3)、在(2)的条件下,坐标轴上是否存在点Q,使△OPQ与△OPB的面积相等.若存在,直接写出点Q的坐标;若不存在,请说明理由.