安徽省芜湖市无为市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
1. 下列各数中是无理数的是( )A、 B、3.14 C、 D、2. 在下列四项调查中,方式正确的是( )A、了解全省中学生每天完成课后作业所用的时间,采用全面调查的方式 B、为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 C、了解一批水稻种子的发芽率,采用全面调查的方式 D、了解全省中学生的视力情况,采用抽样调查的方式3. 如图,下列判断中正确的是( )
 A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么4. 已知m,n满足方程组 ,则m+n的值为( )A、3 B、﹣3 C、﹣2 D、25. 如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至 , 则( )
A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么4. 已知m,n满足方程组 ,则m+n的值为( )A、3 B、﹣3 C、﹣2 D、25. 如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至 , 则( ) A、 , B、 , C、 , D、 ,6. 如图,直线AB与CD相交于E,在∠CEB的平分线上有一点F,FM∥AB.当∠3=10°时,∠F的度数是( )
A、 , B、 , C、 , D、 ,6. 如图,直线AB与CD相交于E,在∠CEB的平分线上有一点F,FM∥AB.当∠3=10°时,∠F的度数是( ) A、82° B、80° C、85° D、83 °7. 如图是由7个形状、大小都相同的小长方形和一块正方形无缝隙拼合而成,则图中阴影部分的面积为( )
A、82° B、80° C、85° D、83 °7. 如图是由7个形状、大小都相同的小长方形和一块正方形无缝隙拼合而成,则图中阴影部分的面积为( ) A、15 B、30 C、36 D、408. 《九章算术》中的方程问题:“五只雀、六只燕,共重 斤(古代 斤= 两),雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕的重量各为多少?”设每只雀、燕的重量各为 两、 两,下列方程组正确的为( )A、 B、 C、 D、9. 如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )A、平行四边形 B、等腰梯形 C、正六边形 D、圆10.
A、15 B、30 C、36 D、408. 《九章算术》中的方程问题:“五只雀、六只燕,共重 斤(古代 斤= 两),雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕的重量各为多少?”设每只雀、燕的重量各为 两、 两,下列方程组正确的为( )A、 B、 C、 D、9. 如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )A、平行四边形 B、等腰梯形 C、正六边形 D、圆10.运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )
 A、x≥11 B、11≤x<23 C、11<x≤23 D、x≤23
A、x≥11 B、11≤x<23 C、11<x≤23 D、x≤23二、填空题
-
11. 计算 .12.
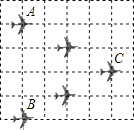
如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是 .
 13. 将含30°的三角板和一把直尺如图放置,测得 , 则的度数是 .
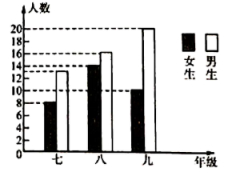
13. 将含30°的三角板和一把直尺如图放置,测得 , 则的度数是 .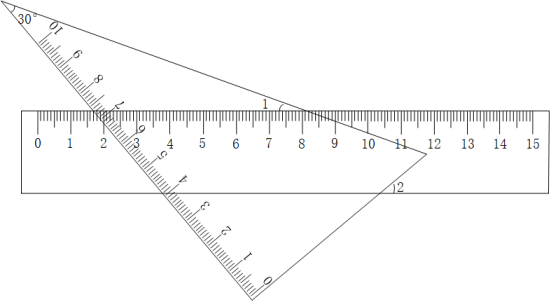 14. 如图,所提供的信息错误的是(填序号).
14. 如图,所提供的信息错误的是(填序号).①七年级学生总数最多
②九年级的男生数是女生数的两倍
③女生总数比男生总数少16人
④八年级的学生总数比九年级的学生总数多
三、解答题
-
15. 解方程组:16. 解不等式组请结合题意填空,完成本题的解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来:
 (4)、原不等式组的解集为 .17. 请将下列证明过程补充完整:
(4)、原不等式组的解集为 .17. 请将下列证明过程补充完整:已知:如图,点P在CD上,已知 , .

求证:
证明:∵(已知)
∴▲ // ▲ ( )
∴ ▲ ( )
又∵(已知)
∴ ▲
即 ▲ (等式的性质)
∴//(内错角相等,两直线平行)
∴( )
18. 如图,在的方格内,填写了一些代数式和数.在图中各行、各列及斜对角上的三个数之和都相等,请你求出x,y的值及左下角的方格内应填的数.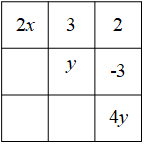 19. 如图,// , , EF平分 , , 垂足为点H,求的度数.
19. 如图,// , , EF平分 , , 垂足为点H,求的度数. 20. 据说,我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口而出:39.你知道他是怎么快速准确地计算出来的吗?请研究解决下列问题:(1)、已知 , 且x为整数.
20. 据说,我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口而出:39.你知道他是怎么快速准确地计算出来的吗?请研究解决下列问题:(1)、已知 , 且x为整数.∵ ,
∴x一定是一个两位数;
∵10648的个位数字是8,
∴x的个位数字一定是;
划去10648后面的三位648得10,
∵ ,
∴x的十位数字一定是;
∴ .
(2)、 , 且y为整数,按照以上思考方法,请你求出y的值.21. 2022年3月28日是我国第27个“全国中小学生安全教育日”,某校为提高学生交通、防溺水、消防安全、饮食安全、用电安全、网络安全等安全意识,组织全体学生参加安全知识测试,从中抽取了部分学生成绩(成绩为整数)进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如表(未完成),解答下列问题: (1)、样本容量为 , 频数分布直方图中;(2)、补全频数分布直方图;(3)、扇形统计图中E小组所对应的扇形圆心角的度数为°;(4)、若成绩在80分以上(不含80分)为优秀,全校共有3000名学生,估计成绩优秀的学生有多少名?22. 如图所示,在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是 , , , 先将向上平移3个单位长度,再向右平移2个单位长度,得到 .
(1)、样本容量为 , 频数分布直方图中;(2)、补全频数分布直方图;(3)、扇形统计图中E小组所对应的扇形圆心角的度数为°;(4)、若成绩在80分以上(不含80分)为优秀,全校共有3000名学生,估计成绩优秀的学生有多少名?22. 如图所示,在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是 , , , 先将向上平移3个单位长度,再向右平移2个单位长度,得到 .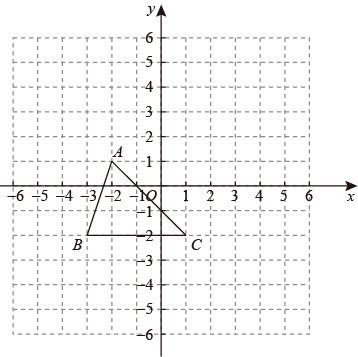 (1)、在图中画出 .(2)、写出点的坐标.(3)、若y轴上有一点P,使与面积相等,求出P点的坐标.23. 某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:
(1)、在图中画出 .(2)、写出点的坐标.(3)、若y轴上有一点P,使与面积相等,求出P点的坐标.23. 某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)、求A、B两种型号的电风扇的销售单价;(2)、若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?(3)、在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.