安徽省阜阳市太和县2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-09-07 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数 $- 1$ ， $- \sqrt{2}$ ，0， $\frac{1}{4}$ 中，最小的实数是（）．

A、 $- 1$ B、 $\frac{1}{4}$ C、0 D、 $- \sqrt{2}$

查看试题解析
2. 下列各选项的结果表示的数中，不是无理数的是（）

A、如图，直径为单位1的圆从数轴上的原点沿着数轴无滑动地顺时针滚动一周到达点A，点A表示的数 B、5的算术平方根 C、9的立方根 D、 $\sqrt{144}$

查看试题解析
3.
如图，要把河中的水引到水池A中，应在河岸B处（AB⊥CD）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是（　　）

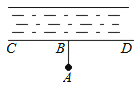A、两点之间线段最短 B、点到直线的距离 C、两点确定一条直线 D、垂线段最短

查看试题解析
4. 如图，OC是∠AOB的角平分线，l//OB，若∠1=52°，则∠2的度数为（）

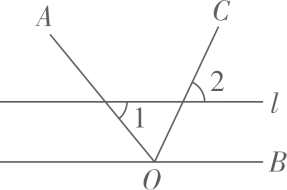A、52° B、54° C、64° D、69°

查看试题解析
5. 下列调查中，适宜采用全面调查（普查）方式的是（　　）

A、调查市场上老酸奶的质量情况　　 B、调查某品牌圆珠笔芯的使用寿命　　 C、调查乘坐飞机的旅客是否携带了危禁物品 D、调查我市市民对伦敦奥运会吉祥物的知晓率

查看试题解析
6. 把一根长17m的钢管截成2m和3m长两种不同规格的钢管，且不造成浪费，你有几种不同的截法（）

A、1种 B、2 种 C、3种 D、4种

查看试题解析
7. 下列命题中，假命题是（）

A、对顶角相等． B、在同一平面内，若 $a ∥ b$ ， $b ∥ c$ ，则 $a ∥ c$ ． C、两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行． D、如果一个角的两边分别平行于另一个角的两边，那么这两个角相等．

查看试题解析
8. 以方程组 ${\begin{array}{l} x + y = - 2 \\ x - y = - 1 \end{array}$ 的解为坐标的点 $(x ， y)$ 在平面直角坐标系中位于第（）象限

A、I B、Ⅱ C、Ⅲ D、Ⅳ

查看试题解析
9. 《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何?”译文大致是：“用一根绳子去量一根木条，绳子剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺?”如果设木条长 $x$ 尺，绳子长 $y$ 尺，根据题意列方程组正确的是（）

A、 ${\begin{array}{l} x + 4.5 = y ， \\ \frac{y}{2} + 1 = x \end{array}$ B、 ${\begin{array}{l} x = y + 4.5 ， \\ \frac{y}{2} + 1 = x \end{array}$ C、 ${\begin{array}{l} x = y + 4.5 ， \\ y = \frac{x}{2} + 1 \end{array}$ D、 ${\begin{array}{l} x + 4.5 = y ， \\ x = \frac{y}{2} - 1 \end{array}$

查看试题解析
10. 若关于x的不等式 $3 x + a \leq 2$ 只有2个正整数解，则a的取值范围为（）

A、 $- 7 < a < - 4$ B、 $- 7 \leq a \leq - 4$ C、 $- 7 \leq a < - 4$ D、 $- 7 < a \leq - 4$

查看试题解析

二、填空题

11. 64的平方根是．

查看试题解析
12. 点 $P (- \sqrt{3} ， 5)$ 到y轴距离为．

查看试题解析
13. 如图是故宫部分建筑的分布示意图，分别以正东、正北方向为x轴，y轴的正方向建立平面直角坐标系．若慈宁宫的坐标为（－2，－2），紫禁城角楼的坐标为（3，1），那么太和殿的坐标为．

查看试题解析
14. 已知：如图，点D是射线AB上一动点，连接CD，过点D作 $D E ∥ B C$ 交直线AC于点E，若 $∠ A B C = 84 °$ ， $∠ C D E = 20 °$ ，则 $∠ A D C$ 的度数为．

查看试题解析

三、解答题

15. 计算： $\sqrt[3]{8} + | 3 - \sqrt{2} | - \sqrt{25} + \sqrt{2}$

查看试题解析
16. 求不等式 $4 (x + 2) > 5 (x - 1)$ ，并把解集在数轴上表示出来．

查看试题解析
17. 如图， $A D ⊥ B C$ 于点D， $E G ⊥ B C$ 于点G，若 $∠ E = ∠ 1$ ，试说明： $∠ 2 = ∠ 3$ ．下面是推理过程，请将推理过程补充完整．
∵ $A D ⊥ B C$ 于点D， $E G ⊥ B C$ 于点G（已知），
∴ $∠ A D C = ∠ E G C = 90 °$ （垂直的定义）
∴ $A D ∥ E G$ （          ）
∴ $∠ 1 = ∠ 2$ （          ）
∵ $∠ E = ∠ 1$ （已知），
∴ $∠ E = ∠ 2$ （          ）
又∵ $A D ∥ E G$ （已证），
∴ $∠ E = ∠ 3$ （          ）
∴ $∠ 2 = ∠ 3$ （等量代换）．

查看试题解析
18. 在平面直角坐标系中，已知点P的坐标为 $(2 a + 6 ， a - 3)$

(1)、若点P在y轴上，求点P的坐标；

(2)、若点P在第四象限，求a的取值范围．

查看试题解析
19. 已知： $△ A B C$ 在直角坐标平面内，三个顶点的坐标分别为 $A (0 ， 3)$ ， $B (3 ， 4)$ ， $C (2 ， 2)$ （正方形网格中每个小正方形的边长是一个单位长度）

(1)、现将 $△ A B C$ 平移，使点A变换为点 $D (- 3 ， - 2)$ ，点E、F分别是B、C的对应点，请画出平移后的 $△ D E F$ ；

(2)、写出点E、F的坐标；

(3)、若连接AD，CF，则这两条线段之间的数量关系与位置关系是、．

查看试题解析
20. 先阅读，再解方程组.
解方程组 ${\begin{array}{l} x - y - 1 = 0 ， ① \\ 4 (x - y) - y = 5 ② \end{array}$ 时，可由①得 $x - y = 1$ ③，然后再将③代入②，得 $4 \times 1 - y = 5$ ，解得 $y = - 1$ ，从而进一步得 ${\begin{array}{l} x = 0 ， \\ y = - 1 . \end{array}$ 这种方法被称为“整体代入法”.

请用上述方法解方程组 ${\begin{array}{l} 2 x - 3 y - 2 = 0 ， \\ \frac{2 x - 3 y + 5}{7} + 2 y = 9 . \end{array}$

查看试题解析
21. 为庆祝中国共产党建党100周年，某校开展了以“学习百年党史，汇聚团结伟力”为主题的知识竞赛，竞赛结束后随机抽取了部分学生成绩进行统计，按成绩分成A，B，C，D，E五个等级，并绘制了如下不完整的统计图．请结合统计图，解答下列问题：
等级
成绩x
A
50≤x＜60
B
60≤x＜70
C
70≤x＜80
D
80≤x＜90
E
90≤x≤100

(1)、本次调查一共随机抽取了名学生的成绩，频数分布直方图中m=；

(2)、补全学生成绩频数分布直方图；

(3)、若成绩在80分及以上为优秀，全校共有2000名学生，估计成绩优秀的学生有多少人？

查看试题解析

22. 今年6月以来，我国多地遭遇强降雨，引发洪涝灾害，人民的生活受到了极大的影响，“一方有难，八方支援”，某市筹集了大量的生活物资，用A，B两种型号的货车，分两批运往受灾严重的地区，具体运算情况如下：

	第一批	第二批
A型货车的辆数（单位：辆）	1	2
B型货车的辆数（单位：辆）	3	5
累计运送货物的吨数（单位：吨）	28	50
备注：第一批、第二批每辆货车均满载

(1)、求A，B两种型号货车每辆满载分别能运多少吨生活物资；

(2)、该市后续又筹集了62.4吨生活物资，现已联系了3辆A型号货车，试问至少还需联系多少辆B型号货车才能一次性将这批生活物资运往目的地．

查看试题解析

23. 在综合与实践课上，老师让同学们以“两条平行线 $A B ， C D$ 和一块含 $60 °$ 角的直角三角尺 $E F G (∠ E F G = 90 ° ， ∠ E G F = 60 °)$ ”为主题开展数学活动.

(1)、如图1，若三角尺的 $60 °$ 角的顶点G放在 $C D$ 上，若 $∠ 2 = 2 ∠ 1$ ，求 $∠ 1$ 的度数；

(2)、如图2，小颓把三角尺的两个锐角的顶点E，G分别放在 $A B$ 和 $C D$ 上，请你探案并说明 $∠ A E F$ 与 $∠ F G C$ 间的数量关系；

(3)、如图3，小亮把三角尺的直角顶点F放在 $C D$ 上， $30 °$ 角的顶点E落在 $A B$ 上.若 $∠ A E G = α ， ∠ C F G = β$ ，则 $∠ A E G$ 与 $∠ C F G$ 的数量关系是什么？用含 $α ， β$ 的式子表示并说明理由.

查看试题解析

等级	成绩x
A	50≤x＜60
B	60≤x＜70
C	70≤x＜80
D	80≤x＜90
E	90≤x≤100