黑龙江省齐齐哈尔市依安县2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-09-07 类型：期末考试

进入出卷网下载

一、单选题

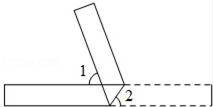
1. $\sqrt{16}$ 的算术平方根是（）

A、4 B、±2 C、2 D、 $\sqrt{2}$

查看试题解析
2. 如果a<b，c<0，那么下列不等式中不成立的是（）

A、a+c<b+c B、ac>bc C、ac+1> bc+1 D、ac²>bc²

查看试题解析
3. 已知平面直角坐标系中，O为坐标原点，点 $A (- 5 ， 4)$ ， $B (x ， y)$ ，将线段A $B$ 平移，使A与O重合，此时B点的对应点 $B^{'}$ 坐标为（2，-1），则 $B$ 点的坐标是（）

A、 $(7 ， - 5)$ B、 $(3 ， - 3)$ C、 $(- 3 ， 3)$ D、 $(- 7 ， 5)$

查看试题解析
4. 如图，将一张矩形纸片折叠，若∠1＝80°，则∠2的度数是（　　）

A、50° B、60° C、70° D、80°

查看试题解析
5. 在平面直角坐标系中，第四象限的点P到x轴的距离为3，到y轴的距离为5，则点P的坐标为（）

A、（﹣3，5） B、（﹣5，3） C、（5，﹣3） D、（3，﹣5）

查看试题解析
6. 要调查下列问题，适合采用全面调查的是（）

A、中央电视台《开学第一课》的收视率 B、天和核心舱的零部件质量 C、汝南县居民6月份人均网上购物的次数 D、某品牌新能源汽车的最大续航历程

查看试题解析
7. 小明带15元去学习用品商店购买A，B，C三种学习用品，其中A，B，C三种学习用品的单价分别为5元、3元、1元，要求每种学习用品至少买一件且A种学习用品最多买两件，若15元刚好用完，则小明的购买方案共有（）

A、3种 B、4种 C、5种 D、6种

查看试题解析
8. 有下列命题：①两条直线被第三条直线所截，同位角相等；②0.1的算术平方根是0.01；③算术平方根等于它本身的数是1；④如果点 $P (3 - 2 n ， 1)$ 到两坐标轴的距离相等，则 $n = 1$ ；⑤若 $a^{2} = b^{2}$ ，则 $a = b$ ；⑥若 $\sqrt[3]{a} = \sqrt[3]{b}$ ，则 $a = b$ 其中假命题的个数是（）

A、1个 B、3个 C、5个 D、6个

查看试题解析
9. 如图，直线 $a / / b$ ，直线 $c$ 与直线 $a$ ， $b$ 分别交于点 $A$ ，点 $B$ ， $A C ⊥ A B$ 于点 $A$ ，交直线 $b$ 于点 $C$ ．如果 $∠ 1 = 34 °$ ，那么 $∠ 2$ 的度数为（）

A、 $34 °$ B、 $56 °$ C、 $66 °$ D、 $146 °$

查看试题解析
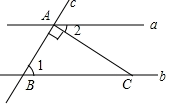10. 若不等式组 ${\begin{array}{l} x > a \\ 5 + 2 x < 3 x + 1 \end{array}$ 的解集为x＞4，则a的取值范围是（）

A、a＞4 B、a＜4 C、a≤4 D、a≥4

查看试题解析

二、填空题

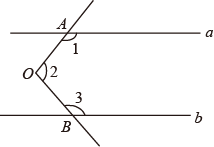
11. －5的相反数是．

查看试题解析
12. 若实数 m，n 满足 ${(m - 3)}^{2} + \sqrt{n - 2} = 0$ ，则 $m^{n}$ ＝．

查看试题解析
13. 已知点A(-5，0)，点B(3，0)，点C在y轴上，△ABC的面积为12，则点C的坐标为．

查看试题解析
14. 如图，直线a与∠AOB的一边射线OA相交，∠1＝130°，向下平移直线a得到直线b，与∠AOB的另一边射线OB相交，则∠2+∠3＝．

查看试题解析
15. 在平面直角坐标系中，已知点M（m﹣1，2m+3）在第二象限，则m的取值范围是．

查看试题解析
16. m的平方根是n-3和n-7，那么mn= ．

查看试题解析
17. 如图，正方形 $A_{1} A_{2} A_{3} A_{4}$ ， $A_{5} A_{6} A_{7} A_{8}$ ， $A_{9} A_{10} A_{11} A_{12}$ ， …，（每个正方形从第三象限的顶点开始，按顺时针方向顺序，依次 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， $A_{4}$ ， $A_{5}$ ， $A_{6}$ ， $A_{7}$ ， $A_{8}$ ， $A_{9}$ ， $A_{10}$ ， $A_{11}$ ， $A_{12}$ ；…）的中心均在坐标原点O，各边均与x轴或y轴平行，若它们的边长依次是2，4，6…，则顶点 $A_{20}$ 的坐标为．

查看试题解析

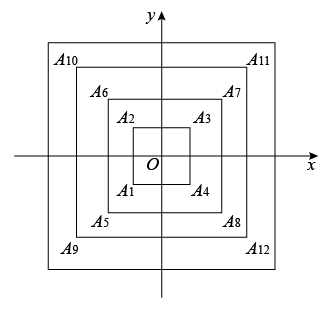
三、解答题

18.

(1)、计算 $\sqrt[3]{8} - \sqrt{4} + | 1 - \sqrt{2} |$

(2)、解方程组 ${\begin{array}{l} 3 x - y = 13 \\ 5 x + 2 y = 7 \end{array}$

查看试题解析
19. 解不等式组： ${\begin{array}{l} 2 (x + 1) < x + 4 \\ \frac{x - 1}{3} - \frac{3 x - 7}{6} \leq 1 \end{array}$ 并把解集在数轴上表示出来．

查看试题解析

20. 促进青少年健康成长是实施“健康中国”战略的重要内容．为了引导学生积极参与体育运动，某校举办了一分钟跳绳比赛，随机抽取了40名学生一分钟跳绳的次数进行调查统计，并根据调查统计结果绘制了如表格和统计图：

等级	次数	频率
不合格	100≤x $<$ 120	a
合格	120≤x $<$ 140	b
良好	140≤x $<$ 160
优秀	160≤x $<$ 180

请结合上述信息完成下列问题：

(1)、a＝， b＝；

(2)、请补全频数分布直方图；

(3)、在扇形统计图中，“良好”等级对应的圆心角的度数是；

(4)、若该校有2000名学生，根据抽样调查结果，请估计该校学生一分钟跳绳次数达到合格及以上的人数．

查看试题解析

21. 如图，三角形ABC在平面直角坐标系中，完成下列问题：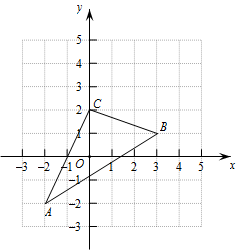

(1)、请写出三角形ABC各顶点的坐标；

(2)、求出三角形ABC的面积；

(3)、若把 $△ A B C$ 向上平移2个单位，再向左平移1个单位得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标；

查看试题解析
22. 在城市创卫工作中为“保护好环境，拒绝冒黑烟”，某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车，计划购买A型和B型两种环保节能公交车共10辆，若购买A型公交车3辆，B型公交车2辆，共需600万元；若购买A型公交车2辆，B型公交车3辆，共需650万元．

(1)、求购买A型和B型公交车每辆各需多少万元？

(2)、预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？哪种购车方案总费用最少？最少总费用是多少？

查看试题解析
23. 点E在射线DA上，点F、G为射线BC上两个动点，满足 $∠ D B F = ∠ D E F$ ， $∠ B D G = ∠ B G D$ ， DG平分∠BDE．

(1)、如图1，当点G在F右侧时，求证： $B D ∥ E F$ ；

(2)、如图2，当点G在F左侧时，求证： $∠ D G E = ∠ B D G + ∠ F E G$ ；

(3)、如图3，在（2）的条件下，P为BD延长线上一点，DM平分∠BDG，交BC于点M，DN平分∠PDM，交EF于点N，连接NG，若 $D G ⊥ N G$ ， $∠ D B F - ∠ D N G = ∠ E D N$ ，则∠DBF的度数为．

查看试题解析