黑龙江省佳木斯市前进区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-09-07 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数- $\sqrt{3}$ ， 3.51015， $\frac{π}{2}$ ， $\sqrt[3]{125}$ ， 0.131131113……（每两个3之间递增一个1）中，无理数的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
2. 若 $x^{| m - 2 |}$ +（m-1）y=6是关于x，y的二元一次方程，则m的值是（）

A、3 B、1 C、任意数 D、1或3

查看试题解析
3. 已知点A（a-1，a-3）在x轴上，则点B（2a-3，3a-2）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图，图1是长方形纸带，将纸带沿EF折叠成图2，再沿BF折叠成图3，若图3中∠CFE=120°，则图1中的∠DEF的度数是（）

A、30° B、20° C、40° D、15°

查看试题解析
5. 如果a＞b，则下列结论中正确的是（）

A、ac²>bc² B、b>-a C、-2a+3<-2b+3 D、2a<2b

查看试题解析
6. 下列调查：①调查洗衣机的使用寿命；②调查“神舟十四号载人飞船”的零部件；③调查人们保护地球环境的意识；④调查全国初中生的视力情况．其中适合抽样调查的是（）

A、①②③④ B、①②③ C、①②④ D、①③④

查看试题解析
7. 不等式组 ${\begin{array}{l} 3 - 2 x > 0 \\ 2 x - 7 \leq 4 x + 7 \end{array}$ 的非负整数解的个数是（）

A、1个 B、0 C、2个 D、无数个

查看试题解析
8. 下列命题是真命题的是（）

A、两条直线被第三条直线所截，同位角相等． B、同一平面内，过一点有且只有一条直线与已知直线垂直． C、同一平面内，过一点有且只有一条直线与已知直线平行． D、互补的两个角是邻补角．

查看试题解析
9. 小丽同学带11元钱去买钢笔和笔记本（两种文具都买），钢笔每支3元，笔记本每本1元，那么钢笔能买（）

A、1支 B、1支或2支或3支 C、2支 D、2支或3支

查看试题解析
10. 如图，将一副三角板按如图放置，则下列结论：①∠1=∠3，②如果∠2=30°时，则有AC $∥$ DE，③如果∠2=30°，必有∠4=45°，④如果∠2=30°，则AB⊥DE．其中正确的有（）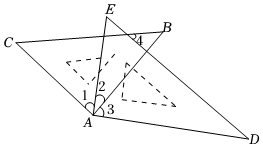

A、①②③ B、②③④ C、①②④ D、①②③④

查看试题解析

二、填空题

11. $\sqrt{9}$ 的平方根是

查看试题解析
12. 若式子 $\sqrt{x - 3}$ 有意义，则实数 $x$ 的取值范围是.

查看试题解析
13. 如图，在四边形ABCD中，在不添加任何辅助线和字母的情况下，添加一个条件，使AB $∥$ DC．（填一个即可）

查看试题解析
14. ∠α与∠β的两边分别平行，且∠α比∠β大30°，则∠α= ．

查看试题解析
15. 如果不等式组 ${\begin{array}{l} 2 x - 10 < 0 \\ x - a \geq 0 \end{array}$ ，只有三个整数解，a的取值范围是．

查看试题解析
16. 把一筐苹果分给几个学生，如果每人分3个，那么余8个；如果每人分5个，那么最后一人分到，但不足3个．设学生有x人，列不等式组为．

查看试题解析
17. 若不等式ax-2＞0的解集为x＜-2，则关于 $y$ 的方程 $a y + 2 = 0$ 的解为.

查看试题解析
18. 若4+ $\sqrt{15}$ 的小数部分是a，7- $\sqrt{15}$ 的小数部分是b，则a+b的值是．

查看试题解析
19. 已知线段AB∥y轴，点A（1，-3），B（m，n），且AB=5时，点B的坐标为．

查看试题解析
20. 如图，在平面直角坐标系中，点A的坐标为（1，0），点A第₁次跳动至点A₁（-1，1），第2次向右跳动3个单位长度至点A₂（2，1），第3次跳动至点A₃（-2，2），第4次向右跳动5个单位长度至点A₄（3，2）……依此规律跳动下去，第50次跳动至点A₅₀的坐标是．

查看试题解析

三、解答题

21. 解下列方程组

(1)、 ${\begin{array}{l} 4 x - 3 y = 11 \\ 2 x + y = 13 \end{array}$

(2)、 ${\begin{array}{l} x + y + z = 6 \\ y - z = 4 \\ x - 2 y - z = 3 \end{array}$

查看试题解析
22. 解下列不等式（组），并把解集在数轴上表示出来．

(1)、1+ $\frac{x}{3}$ >5- $\frac{x - 2}{2}$

(2)、 ${\begin{array}{l} 3 (x - 2) \geq x - 4 \\ \frac{2 x + 1}{3} > x - 1 \end{array}$

查看试题解析
23. 如图在平面直角坐标系中，每个小正方形的边长都是1个单位．

(1)、将三角形ABC向下平移4个单位，再向左平移2个单位，得到三角形A₁B₁C₁ ，请画出三角形A₁B₁C₁

(2)、请直接写出B₁、C₁的坐标．

(3)、求出线段AC扫过部分的面积．（重叠部分不重复计算）

查看试题解析
24. 暑期将至，学校组织学生进行“防溺水”安全知识竞赛，老师从中随机抽取了部分学生的成绩（得分取整数，满分为100分），整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图．其中A组的频数a比B组的频数b小15．请根据以上信息，解答下列问题：

(1)、本次共抽取名学生，b的值为；

(2)、在扇形统计图中，n= ， E组所占比例为%；

(3)、补全频数分布直方图；

(4)、若全校共有2500名学生，请根据抽样调查的结果，估计成绩在80分以上的学生人数．

查看试题解析
25. 完成下列的推理说明：已知：如图，BE//CF，BE、 $C F$ 分别平分 $∠ A B C$ 和 $∠ B C D$ ．
求证：AB//CD．
证明： $∵ B E$ 、 $C F$ 分别平分 $∠ A B C$ 和 $∠ B C D$ （已知）
$∴ ∠ 1 = \frac{1}{2} ∠$             ▲        ． $∠ 2 = \frac{1}{2} ∠$             ▲       （      ）
BE//CF（      ）
$∴ ∠ 1 = ∠ 2$ （      ）
$∴ \frac{1}{2} ∠ A B C = \frac{1}{2} ∠ B C D$ （      ）
$∴ ∠ A B C = ∠ B C D$ （等式的性质）
AB//CD（      ）

查看试题解析
26. 七年级同学解决平行线问题时，遇到这样的问题，请你帮忙解决：已知AB∥CD，

(1)、如图1，猜想∠AEC，∠BAE，∠DCE之间有什么数量关系不必说明理由；

(2)、如图2，BE平分∠ABC，DE平分∠ADC．BE、DE所在直线交于点E，若∠FAD=40°，∠ABC=50°，求∠BED的度数；

(3)、将图（2）中的线段BC沿DC所在的直线平移，使得点B在点A的右侧，∠FAD=m°，∠ABC=n°，其他条件不变，得到图3，请直接写出∠BED的度数（用含m，n的式子表示）．

查看试题解析
27. 某工厂有甲种原料66千克．乙种原料66.4千克，现计划用这两种原料生产A、B两种型号的产品共90件、已知每件A型号下需要甲种原料0.5千克，乙种原料0.8千克；每件B型号产品需要甲种原料1.2千克，乙种原料0.6千克．

(1)、该工厂有哪几种生产方案？

(2)、在这批产品全部售出的条件下，若1件A型号产品获利30元，1件B型号产品获利20元，（1）中哪种方案获利最大？最大利润是多少？

(3)、在（2）的条件下，工厂决定将所获利润的25%全部用于再次购进甲、乙两种（两种原料都有）原料，且购进每种原料的数量均为正整数．若甲种原料每千克35元，乙种原料每千克55元．请直接写出购买甲、乙两种原料各多少千克

查看试题解析
28. 如图，在平面直角坐标系中，点A，B的坐标分别为（-1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．

(1)、直接写出点C，D的坐标；

(2)、若在y轴上存在点M，连接MA，MB，使SΔMAB =S_四_边_形ABDC，求出点M的坐标；

(3)、若点P在线段BD之间时（不与B，D重合），连接PC，PO．求SΔCDP +SΔBOP 的取值范围．

查看试题解析