黑龙江省佳木斯市抚远市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-09-07 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数 $\frac{1}{3} ， 0.10101 ， \sqrt{6} ， \sqrt[3]{27} ， \sqrt{9}$ 中，无理数共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下面四个图案中，能由如图经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 若 $a > b$ ，则下列不等式一定成立的是：（）

A、 $a + 1 > b + 3$ B、 $a - 2 < b - 2$ C、 $\frac{a}{3} > \frac{b}{3}$ D、 $- a > - b$

查看试题解析
4. 下列调查方式，你认为最合适的是（）

A、旅客上飞机前的安检，采用抽样调查方式 B、了解端午节到延庆旅游的人数，采用抽样调查方式 C、了解北京市中学生的用眼卫生情况，采用全面调查方式 D、了解一批手机电池的使用寿命，采用全面调查方式

查看试题解析
5. 如图，直线 $a ∥ b$ ，直线 $A B ⊥ A C$ ，若 $∠ 1 = 50 °$ ，则 $∠ 2$ 的度数为（）

A、50° B、45° C、40° D、30°

查看试题解析
6. 在用代入消元法解二元一次方程组 ${\begin{array}{l} x + 3 y = - 2 \\ 3 x - 4 y = 6 \end{array}$ 时，消去未知数x后，得到的方程为（）

A、 $3 (- 2 - 3 y) - 4 y = 6$ B、 $3 (- 2 - 3 y) + 4 y = 6$ C、 $3 (- 2 + 3 y) - 4 y = 6$ D、 $3 (- 2 + 3 y) + 4 y = 6$

查看试题解析
7. 某市今年共有6万名考生参加中考，为了了解这6万名考生的数学成绩，从中抽取了1000名考生的数学成绩进行统计分析，以下说法：
①这种调查采用了抽样调查的方式；②6万名考生是总体；③1000名考生的数学成绩是总体的一个样本；④样本容量是1000名．
其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 在平面直角坐标系中，将点 $A (- 3 ， - 2)$ 向上平移4个单位长度得到点B，则点B关于x轴的对称点 $B^{'}$ 的坐标为（）

A、 $(3 ， 2)$ B、 $(- 3 ， - 2)$ C、 $(- 3 ， 2)$ D、 $(3 ， - 2)$

查看试题解析
9. 已知不等式组 ${\begin{array}{l} x + a > 1 ， \\ 2 x - b < 2 \end{array}$ 解集为 $- 2 < x < 3$ ，则 ${(a - b)}^{2022}$ 的值为（）

A、1 B、2022 C、-1 D、-2022

查看试题解析
10. 小明计划用100元钱在京东商城购买价格分别为6元和8元的两种商品，则在钱全部用完的前提下，可供小明选择的方案有（）

A、3种 B、4种 C、5种 D、6种

查看试题解析

二、填空题

11. 已知 $2 x - 1$ 的算术平方根是5，则5x-1的立方根是．

查看试题解析
12. 已知x，y满足方程组 ${\begin{array}{l} x + 2 y = - 2 \\ 2 x + y = 3 \end{array}$ ，则 $x - y$ 的值为．

查看试题解析
13. 已知点 $P (x ， y)$ 的坐标满足 $| x | = 3$ ， $\sqrt{y} = 2$ ，且 $x y < 0$ ，则点 $P$ 的坐标是

查看试题解析
14. AB∥CD ， ∠1＝58°，FG平分∠EFD ，则∠FGB的度数为．

查看试题解析
15. 为了解八年级女生的体能情况，随机抽查了30名女生，测试了1分钟仰卧起坐的个数，并绘制成如图所示的频数分布直方图（每组含前一个边界，不含后个边界），则个数不低于38的有人．

查看试题解析
16. 若 $3 m - 5 x^{3 + m} > 4$ 是关于x的一元一次不等式，则该不等式的解集是．

查看试题解析
17. 如图，两个边长为5的正方形拼合成一个长方形，则图中阴影部分的面积是.

查看试题解析
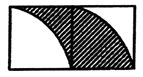18. 已知关于x，y的方程组 ${\begin{array}{l} x + 2 y = 2 m - 5 ， \\ x - 2 y = 3 - 4 m \end{array}$ 的解满足 $x < 1$ ， $y < 2$ ，则m的取值范围为．

查看试题解析
19. 某种出租车的收费标准是起步价8元（即距离不超过3km，都付8元车费），超过3km以后，每增加1km，加收1.2元（不足1km按1km计），若某人乘这种出租车从甲地到乙地经过的路程是xkm，共付车费14元，那么x的最大值是．

查看试题解析
20. 如图，在平面直角坐标系中，一个质点P从点 $P_{1} (- 1 ， 0)$ 出发，运动到点 $P_{2} (- 1 ， - 1)$ ，运动到点 $P_{3} (1 ， - 1)$ ，运动到点 $P_{4} (1 ， 1)$ ，运动到点 $P_{5} (- 2 ， 1)$ ，运动到点 $P_{6} (- 2 ， - 2)$ ……按照上述规律运动下去，则点 $P_{2022}$ 的坐标为．

查看试题解析

三、解答题

21. 解方程组或不等式组：

(1)、 ${\begin{array}{l} x + y = 2 ， ① \\ 3 x + y = 4 ； ② \end{array}$

(2)、 ${\begin{array}{l} x - 4 \leq 2 (x - 1) ， ① \\ \frac{1}{2} (x + 3) > x + 1 . ② \end{array}$

查看试题解析
22. 已知a为 $\sqrt{17}$ 的整数部分， $b - 1$ 是121的算术平方根，求 $\sqrt{a + b}$ 的值．

查看试题解析
23. 已知三角形ABC与三角形 $A^{'} B^{'} C^{'}$ 在平面直角坐标系中的位置如图所示，且三角形 $A^{'} B^{'} C^{'}$ 是由三角形ABC平移得到的．

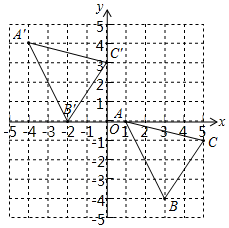(1)、分别写出点B， $B^{'}$ 的坐标；B ， $B^{'}$ ；

(2)、若 $P (a ， b)$ 是三角形ABC内部的一点．则平移后的三角形 $A^{'} B^{'} C^{'}$ 内的对应点 $P^{'}$ 的坐标为．

(3)、求三角形ABC的面积．

查看试题解析
24. 如图，已知 $A D ∥ B C$ ， $A B ∥ C D$ ，点E在线段BC的延长线上，AE平分 $∠ B A D$ ，连接DE， $∠ A D C = 2 ∠ C D E$ ， $∠ A E D = 60 °$ ．

(1)、求证 $∠ A B C = ∠ A D C$ ；

(2)、求 $∠ C D E$ 的度数．

查看试题解析
25. 育红学校为了了解学生家长对教育部《关于进一步加强中小学生睡眠管理工作的通知》（以下简称《通知》）的了解程度，随机抽取了该校部分学生家长进行问卷调查，问卷分为A（十分了解），B（了解较多），C（了解较少），D（不了解）四个选项，要求每位被调查家长必选且只能选择其中的一项．在对调查数据进行统计分析时，绘制了如图所示的两幅不完整的统计图，请你依据图中信息解答下列问题：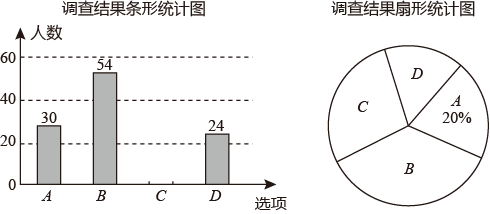

(1)、参与这次学校调查的学生家长共人；

(2)、通过计算将条形统计图补充完整；

(3)、若该校共有2000名学生家长，请估计该校学生家长中对《通知》“十分了解”和“了解较多”的一共约有多少人？

查看试题解析
26. 如图①， $∠ E F H = 90 °$ ，点A，C分别在射线FE和FH上， $A B ∥ C D$ ．

(1)、若 $∠ F A B = 150 °$ ，则 $∠ H C D$ 的度数为；

(2)、小明同学发现，无论 $∠ F A B$ 如何变化， $∠ F A B - ∠ H C D$ 的值始终为定值，并给出了一种证明该发现的辅助线作法：如图②，过点A作 $A M ∥ F H$ ，交CD于点M．请你根据小明同学提供的辅助线，确定该定值，并说明理由；

(3)、如图③，把“ $∠ E F H = 90 °$ ”改为“ $∠ E F H = 120 °$ ”，其他条件保持不变，猜想 $∠ F A B$ 与 $∠ H C D$ 的数量关系，并说明理由．

查看试题解析
27. 为了更好治理河流水质，保护环境，某市治污公司决定购买10台污水处理设备，现有A，B两种型号的设备，其中每台的价格，月处理污水量如表：

A型
B型
价格（万元/台）
a
b
处理污水量（吨/月）
220
180
经调查：购买一台A型设备比购买一台B型设备多3万元，购买2台A型设备比购买3台B型设备少3万元．

(1)、求a，b的值；

(2)、经预算：市治污公司购买污水处理设备的资金不超过100万元，你认为该公司有哪几种购买方案；

(3)、在（2）问的条件下，若每月要求处理的污水量不低于1880吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．

查看试题解析
28. 如图，在平面直角坐标系中，点A，B的坐标分别为 $(a ， 0)$ ， $(b ， 0)$ ，其中a，b满足方程组 ${\begin{array}{l} a + 2 b = 5 ， \\ 3 a + b = 0 ， \end{array}$ 现同时将点A，B向上平移2个单位长度，再向右平移1个单位长度，分别得到点C，D，连接AC，BD，CD．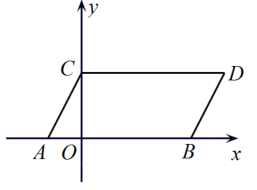

(1)、求点C，D的坐标和四边形ABDC的面积；

(2)、在坐标轴上是否存在点P，使 $S_{三角形 P A C} = S_{四边形 A B D C}$ ？若存在，求点P的坐标；若不存在，请说明理由．

查看试题解析

	A型	B型
价格（万元/台）	a	b
处理污水量（吨/月）	220	180