黑龙江省哈尔滨市双城区2021-2022学年七年级下学期期末考试数学试题

试卷更新日期：2022-09-07 类型：期末考试

进入出卷网下载

一、单选题

1. 16的算术平方根是 $($ $)$

A、4 B、-4 C、±4 D、8

查看试题解析
2. 在平面直角坐标系中，点P（ $- 3$ ， 2）位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列实数中，是无理数的为（　　）

A、0 B、- $\frac{1}{3}$ C、 $\sqrt{2}$ D、3.14

查看试题解析
4. 在2022北京冬奥会上以熊猫为原型的吉祥物“冰墩墩”成了全网“顶流”，通过平移吉祥物“冰墩墩”可以得到的图形是（）．

A、 B、 C、 D、

查看试题解析
5. 已知a＞b，下列关系式中一定正确的是（）

A、 $a^{2}$ > $b^{2}$ B、2a<2b C、a+2<b+2 D、-a<-b

查看试题解析
6. 下列问题中，适合用普查方式的是（）．

A、了解全国七年级同学每周体育锻炼的时间 B、《王牌对王牌》节目的收视率 C、旅客上飞机前的安检 D、调查某批汽车的抗撞击能力

查看试题解析
7. 如图摆放着一副三角板，∠B＝∠EDF＝90°，点E在AC上，点D在BC的延长线上， $E F ∥ B C$ ， ∠A＝30°，∠F＝45°，则∠CED的度数为（）

A、15° B、20° C、30° D、45°

查看试题解析
8. 为了丰富同学们的课余生活，体育委员小强到体育用品商店购买羽毛球拍和乒乓球拍，若购买1副羽毛球拍和1副乒乓球拍共需50元，小强一共用320元购买了6副同样的羽毛球拍和10副同样的乒乓球拍，若设每副羽毛球拍为x元，每副乒乓球拍为y元，列二元一次方程组得（）

A、 ${\begin{array}{l} x + y = 50 \\ 6 (x + y) = 320 \end{array}$ B、 ${\begin{array}{l} x + y = 50 \\ 6 x + 10 y = 320 \end{array}$ C、 ${\begin{array}{l} x + y = 50 \\ 6 x + y = 320 \end{array}$ D、 ${\begin{array}{l} x + y = 50 \\ 10 x + 6 y = 320 \end{array}$

查看试题解析
9. 若关于x的不等式组 ${\begin{matrix} 2 x + 7 > 4 x + 1 \\ x - k < 2 \end{matrix}$ 的解集为x＜3，则k的取值范围为（）

A、k＞1 B、k＜1 C、k≥1 D、k≤1

查看试题解析
10. 如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（）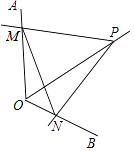

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 若∠A的对顶角是46°，那么∠A的邻补角的度数是．

查看试题解析
12. $\sqrt{2022}$ 的相反数是．

查看试题解析
13. 已知 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ 是方程mx-y=2的解，则m的值是．

查看试题解析
14. 如图，已知AB∥EG，BC∥DE，CD∥EF，则x、y、z三者之间的关系是．

查看试题解析
15. 计算 $\sqrt[3]{8} - \sqrt{4} =$ ．

查看试题解析
16. 把一张对边互相平行的纸条，折成如图所示，EF是折痕，若∠EFB＝32°，则∠BGE＝．

查看试题解析
17. 有50个数据，共分成6组，第1～4组的频数分别为10，8，7，11．第5组的频率是0.16，则第6组的频数是．

查看试题解析
18. 已知直线AB与直线CD相交于点O，∠AOC：∠BOC＝2：1，射线OE⊥CD，则∠AOE的度数为．

查看试题解析
19. 线段 $A B$ 平移后得到 $C D$ ，已知 $A (2 ， 3)$ 的对应点为 $C (- 1 ， 4)$ ，则 $B (3 ， 2)$ 的对应点 $D$ 的坐标为．

查看试题解析
20. 已知10³＝1000，11³＝1331，12³＝1728，13³＝2197，14³＝2744，15³＝3375，…，20³＝8000，21³＝9261，22³＝10648，23³＝12167，24³＝13824，25³＝15625，…，则³＝110592．

查看试题解析

三、解答题

21.

(1)、 $- 1^{2022} - 2 \times \sqrt{9} - | - 3 | + (- 2)^{3}$

(2)、 ${\begin{array}{l} 2 x = 3 - y \\ 3 x + 2 y = 2 \end{array}$

查看试题解析
22. 解不等式组 ${\begin{matrix} 2 (x - 2) \leq 3 x - 3 \\ \frac{x}{3} < \frac{x + 1}{4} \end{matrix}$ 并写出它的所有非负整数解．

查看试题解析
23. 已知：如图，把 $△ A B C$ 向上平移3个单位长度，再向右平移2个单位长度，得到 $△ A^{'} B^{'} C^{'}$ ．

(1)、在图中画出 $△ A^{'} B^{'} C^{'}$ ．

(2)、写出 $A^{'}$ ， $B^{'}$ 的坐标．

(3)、在 $y$ 轴上是否存在一点 $P$ ，使得 $△ B C P$ 与 $△ A B C$ 面积相等？若存在，求出点 $P$ 的坐标；若不存在，说明理由．

查看试题解析
24. 某校开展了为期一周的“敬老爱亲”社会活动，为了解情况，学生会随机调查了部分学生在这次活动中做家务的时间，并将统计的时间（单位：小时）分成5组，A：0.5≤x＜1，B：1≤x＜1.5，C：1.5≤x＜2，D：2≤x＜2.5，E：2.5≤x＜3，制作成两幅不完整的统计图（如图）.

请根据图中提供的信息，解答下列问题：

(1)、学生会随机调查了名学生；

(2)、补全频数分布直方图；

(3)、若全校有1800名学生，估计该校在这次活动中做家务的时间不少于2.5小时的学生有多少人？

查看试题解析
25. 某商店需要购进甲、乙两种商品共180件其进价和售价如表：（注：获利=售价进价）

(1)、若商店计划销售完这批商品后能获利1240元，问甲、乙两种商品应分别购进多少件？

(2)、若商店计划投入资金少于5040元，且销售完这批商品后获利多于1312元，请问有哪几种购货方案？并直接写出其中获利最大的购货方案.

查看试题解析
26. 如图

(1)、如图1， $A B ∥ C D ， ∠ P A B = 130 ° ， ∠ P C D = 120 °$ ，求 $∠ A P C$ 的度数；

(2)、如图2， $A B ∥ C D$ ，点P在射线 $O M$ 上运动，记 $∠ P A B = α ， ∠ P C D = β$ ，当点P在B，D两点之间运动时，请写出 $∠ A P C$ 与 $α ， β$ 之间的数量关系，并说明理由；

(3)、在（2）的条件下，如果点P在B，D两点外侧运动时（点P与点O，B，D三点不重合），请直接写出 $∠ A P C$ 与 $α ， β$ 之间的数量关系．

查看试题解析
27. 如图，在平面直角坐标系中，点A、B的坐标分别为 $A (0 ， a)$ ， $B (b ， 0)$ ，且 $a$ 、 $b$ 满足 $| 2 a - b - 6 | + \sqrt{a + 2 b - 13} = 0$ ，点C在x轴的负半轴上，连接AB、AC．

(1)、如图1，若 $△ A O C$ 的面积是 $△ A O B$ 面积的 $\frac{3}{4}$ 倍，求点C的坐标：

(2)、如图2，点D在AC上，点E在AB上，连接OD，过点E作 $E F ⊥ x$ 轴于点F，若 $∠ 1 + ∠ 2 = 90 °$ ，求证： $O D / / A B$ ；

(3)、在（1）的条件下，点P从点O出发以每秒1个单位长度的速度沿OB方向移动，同时点Q从点A出发以每秒2个单位长度的速度在AO间往返移动，即先沿AO方向移动，到达点O反向移动．设移动的时间为t秒，四边形ACQB与 $△ A B P$ 的面积分别记为 $S_{1}$ 、 $S_{2}$ ，是否存在时间 $t$ ，使 $S_{1} = 4 S_{2}$ ；若存在，求出 $t$ 值；若不存在，请说明理由．

查看试题解析