河北省唐山市路北区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
1. 冬季某天我国三个城市的最高气温分别是﹣10℃,1℃,﹣7℃,它们任意两城市中最高温度相差最大的是A、3℃ B、8℃ C、11℃ D、17℃2. 下列各组数中,互为相反数的是( )A、-(-1)与1 B、(-1)2与1 C、 与1 D、-12与13. 代数式去括号后的结果是( )A、 B、 C、 D、4. 下列计算中结果正确的是( )A、4+5ab=9ab B、6xy﹣x=6y C、3a2b﹣3ba2=0 D、12x3+5x4=17x75. 已知关于x的方程 的解是 ,则a的值是( )A、1 B、 C、 D、-16. 若x2﹣3x﹣2=0,则2x2﹣6x+2020的值为( )A、2021 B、2022 C、2023 D、20247. 若与的差仍是单项式,则的值是( )A、2 B、3 C、4 D、58. 已知二元一次方程4x+5y=5,用含x的代数式表示y , 则可表示为( )A、y=﹣ x+1 B、y=﹣ x﹣1 C、y= x+1 D、y= x﹣19. 已知 , 从顶点O引一条射线 , 若 , 则( )A、20° B、40° C、80° D、40°或80°10. 点在数轴上表示的数为-3,若一个点从点向左移动4个单位长度,此时终点所表示的数是( )A、-7 B、1 C、7 D、-111. 已知 , 则的值为( )A、2019 B、-2019 C、-1 D、112. 如图,将正方体相邻的两个面上分别画出的正方形网格,并分别用图形“
 ”和“〇”在网格内的交点处做上标记,则该正方体的表面展开图是
”和“〇”在网格内的交点处做上标记,则该正方体的表面展开图是 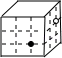 A、
A、 B、
B、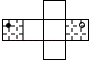 C、
C、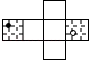 D、
D、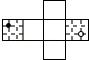 13. 若 ,则下列大小关系中正确的是( )A、b>a>c B、b>c>a C、a>b>c D、c>a>b14. 图中有4根绳子,在绳的两端用力拉,绳子能打成结的是( )A、
13. 若 ,则下列大小关系中正确的是( )A、b>a>c B、b>c>a C、a>b>c D、c>a>b14. 图中有4根绳子,在绳的两端用力拉,绳子能打成结的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
15. 如果a,b互为相反数,x,y互为倒数,那么= .16. 已知方程3x=﹣9的解也是方程x=1+a的解,则代数式a2﹣2a+1的值 .17. 一副三角板按如图方式摆放,且∠1比∠2大40°,则∠2的度数是.
 18. 在标准大气压下, 干净清洁的空气中大约有 个分子,则 干净清洁的空气中大约有个分子.(用科学记数法表示)
18. 在标准大气压下, 干净清洁的空气中大约有 个分子,则 干净清洁的空气中大约有个分子.(用科学记数法表示)三、解答题
-
19. 计算:(1)、 .(2)、 .20. 解方程:21. 如图,点C是线段AB的中点, , ,求CD的长.
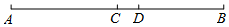 22. 某校组织学生去东南花都进行研学活动.第一天下午,学生队伍从露营地出发,开始向东的方向直走到距离露营地500米处的科普园地.学校联络员也从露营地出发,不停地沿途往返行走,为队伍护行.以向东的方向为正方向,联络员从开始到最后行走的情况依次记录如下(单位:米):+150,-75,+205,-30,+25,-25,+30,-25,+75.(1)、联络员最终有没有到达科普园?如果没有,那么他离科普园还差多少米?(2)、若联络员行走的平均速度为80米/分,请问他此次行程共用了多少分钟?23. 如图,有一块长为20米,宽为10米的长方形土地,现在将三面留出宽都是x米的小路,中间余下的长方形部分做草坪(阴影部分).
22. 某校组织学生去东南花都进行研学活动.第一天下午,学生队伍从露营地出发,开始向东的方向直走到距离露营地500米处的科普园地.学校联络员也从露营地出发,不停地沿途往返行走,为队伍护行.以向东的方向为正方向,联络员从开始到最后行走的情况依次记录如下(单位:米):+150,-75,+205,-30,+25,-25,+30,-25,+75.(1)、联络员最终有没有到达科普园?如果没有,那么他离科普园还差多少米?(2)、若联络员行走的平均速度为80米/分,请问他此次行程共用了多少分钟?23. 如图,有一块长为20米,宽为10米的长方形土地,现在将三面留出宽都是x米的小路,中间余下的长方形部分做草坪(阴影部分). (1)、用含字母x的式子表示:草坪的长a=米,宽b=米;(2)、请求出草坪的周长;(3)、当小路的宽为1米时,草坪的周长是多少?24. 小明的爷爷每天都步行到距离家3.2千米的公园去打太极拳.周日早晨,爷爷出发半小时后,小明发现爷爷忘记带家门钥匙了,小明就骑自行车去给爷爷送钥匙.如果爷爷的速度是4千米/时,小明骑自行车的速度是12千米/时,当小明追上爷爷时,爷爷到公园了吗?
(1)、用含字母x的式子表示:草坪的长a=米,宽b=米;(2)、请求出草坪的周长;(3)、当小路的宽为1米时,草坪的周长是多少?24. 小明的爷爷每天都步行到距离家3.2千米的公园去打太极拳.周日早晨,爷爷出发半小时后,小明发现爷爷忘记带家门钥匙了,小明就骑自行车去给爷爷送钥匙.如果爷爷的速度是4千米/时,小明骑自行车的速度是12千米/时,当小明追上爷爷时,爷爷到公园了吗? 25. 已知是关于x的方程的解.(1)、k的值为 .(2)、在(1)的条件下,已知线段cm,点C是线段AB上一点,且 , 若点D是AC的中点,求线段CD的长;(3)、在(2)的条件下,已知点A所表示的数为 , 点B在点A的右边,有一动点P从点A开始以2个单位长度每秒的速度沿数轴向左匀速运动,同时另一动点Q从点B开始以4个单位长度每秒的速度沿数轴向左匀速运动,当时间为多少秒时,有?26. 如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
25. 已知是关于x的方程的解.(1)、k的值为 .(2)、在(1)的条件下,已知线段cm,点C是线段AB上一点,且 , 若点D是AC的中点,求线段CD的长;(3)、在(2)的条件下,已知点A所表示的数为 , 点B在点A的右边,有一动点P从点A开始以2个单位长度每秒的速度沿数轴向左匀速运动,同时另一动点Q从点B开始以4个单位长度每秒的速度沿数轴向左匀速运动,当时间为多少秒时,有?26. 如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方. (1)、将图1中的三角板绕点O处逆时针旋转至图2,使一边OM在∠BOC的内部.且恰好平分∠BOC,求∠CON与∠AOM的度数.(2)、将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部.请探究:∠CON与∠AOM之间的数量关系,并说明理由.(3)、将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时.直线ON恰好平分锐角∠AOC,则t的值为秒(直接写出结果).
(1)、将图1中的三角板绕点O处逆时针旋转至图2,使一边OM在∠BOC的内部.且恰好平分∠BOC,求∠CON与∠AOM的度数.(2)、将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部.请探究:∠CON与∠AOM之间的数量关系,并说明理由.(3)、将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时.直线ON恰好平分锐角∠AOC,则t的值为秒(直接写出结果).