河北省唐山市乐亭县2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
1. 画的边上的高,正确的是( )A、
 B、
B、 C、
C、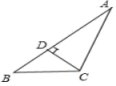 D、
D、 2. 在△ABC中, , , , a的值可能是( )A、1 B、3 C、5 D、73. 若是关于x、y的二元一次方程,那么k的取值满足( )A、 B、 C、 D、4. 墨迹覆盖了等式“
2. 在△ABC中, , , , a的值可能是( )A、1 B、3 C、5 D、73. 若是关于x、y的二元一次方程,那么k的取值满足( )A、 B、 C、 D、4. 墨迹覆盖了等式“ ”中的运算符号,则覆盖的是( ) A、+ B、- C、× D、÷5. 若是关于x、y的方程的一个解,则a的值为( )A、3 B、-3 C、1 D、-16. 用不等式表示“a的2倍与6的差不大于18”为( )A、 B、 C、 D、7. 若 , 则下列式子不一定成立的是( )A、 B、 C、 D、8. 个关于的一元一次不等式组的解集在数轴上的表示如图所示,则该不等式组的解集是( )
”中的运算符号,则覆盖的是( ) A、+ B、- C、× D、÷5. 若是关于x、y的方程的一个解,则a的值为( )A、3 B、-3 C、1 D、-16. 用不等式表示“a的2倍与6的差不大于18”为( )A、 B、 C、 D、7. 若 , 则下列式子不一定成立的是( )A、 B、 C、 D、8. 个关于的一元一次不等式组的解集在数轴上的表示如图所示,则该不等式组的解集是( ) A、 B、 C、 D、9. 如图,点E在BA延长线上,下列条件不能判断的是( )
A、 B、 C、 D、9. 如图,点E在BA延长线上,下列条件不能判断的是( ) A、 B、 C、 D、10. 下列多项式能用完全平方公式进行因式分解的是( )A、 B、 C、 D、11. 如图,直线 , 如果 , , 那么的度数是( )
A、 B、 C、 D、10. 下列多项式能用完全平方公式进行因式分解的是( )A、 B、 C、 D、11. 如图,直线 , 如果 , , 那么的度数是( ) A、31° B、40° C、39° D、70°12. 如图,点D为的角平分线AE延长线上的一点,过点D作于点F,若 , , 则的度数是( )
A、31° B、40° C、39° D、70°12. 如图,点D为的角平分线AE延长线上的一点,过点D作于点F,若 , , 则的度数是( ) A、 B、 C、 D、13. 若 ,则 ( )A、12 B、10 C、8 D、614. 若 , , 则( )A、-3 B、3 C、-4 D、415. 不等式组的整数解有4个,则a的取值可能是( )A、1 B、2 C、-2 D、-316. 如图,在△ABC中,延长CA至点F,使得AF=CA,延长AB至点D,使得BD=2AB,延长BC至点E,使得CE=3CB,连接EF、FD、DE,若S△DEF=36,则S△ABC为( )
A、 B、 C、 D、13. 若 ,则 ( )A、12 B、10 C、8 D、614. 若 , , 则( )A、-3 B、3 C、-4 D、415. 不等式组的整数解有4个,则a的取值可能是( )A、1 B、2 C、-2 D、-316. 如图,在△ABC中,延长CA至点F,使得AF=CA,延长AB至点D,使得BD=2AB,延长BC至点E,使得CE=3CB,连接EF、FD、DE,若S△DEF=36,则S△ABC为( )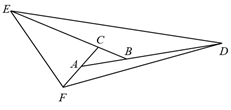 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
17. 在中,若 , , 则是三角形.(填“锐角”、“直角”、或“钝角”)18. 已知 , , 则 .19. 三角形的一个外角是100°,则与它不相邻的两内角平分线夹角(钝角)是 .
 20. 运行程序如图所示,规定:从“输入一个值x”到“结果是否>5”为一次程序操作,如果程序操作进行了两次才停止,那么x的取值范围是 .
20. 运行程序如图所示,规定:从“输入一个值x”到“结果是否>5”为一次程序操作,如果程序操作进行了两次才停止,那么x的取值范围是 .
三、解答题
-
21. 求不等式组的整数解.22. 已知 , .(1)、求和的值;(2)、已知 , 求的值.23. 如图,在△ABC中, , ,
 (1)、求证:;(2)、若DG平分∠ADC, , 求∠EFC的度数.24. 如图1,在一个边长为 的正方形中,剪去一个边长为 的小正方形,再将余下的部分拼成如图2所示的长方形.
(1)、求证:;(2)、若DG平分∠ADC, , 求∠EFC的度数.24. 如图1,在一个边长为 的正方形中,剪去一个边长为 的小正方形,再将余下的部分拼成如图2所示的长方形.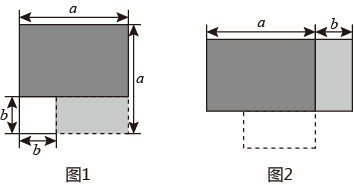 (1)、(观察)
(1)、(观察)比较两图中阴影部分的面积,可以得到等式:(用字母 , 表示);
(2)、(应用)计算: ;
(3)、(拓展)已知 , ,求 的值.
