河北省承德市围场县2021-2022学年七年级下学期期末考试数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
1. 如图,直线AB与直线CD相交于点O,其中∠AOC的对顶角是( )
 A、∠AOD B、∠BOD C、∠BOC D、∠AOD和∠BOC2. 下列方程组中,是二元一次方程组的是( )A、 B、 C、 D、3. 下列选项中的整数,与 最接近的是( )A、3 B、4 C、5 D、64. 若点 在第二象限内,则点 ( )在( )A、 轴正半轴上 B、 轴负半轴上 C、 轴正半轴上 D、 轴负半轴上5. 若 , 则下列不等式中错误的是( )A、 B、 C、 D、6. 国务院在2020年11月1日零时开展了第七次全国人口普查,人口调查采用普查方式的理由是( )A、人口调查的数目不太大 B、受条件限制,无法进行抽样调查 C、人口调查具有破坏性 D、人口调查需要获得全面准确的信息7. 不等式 的非负整数解有( )A、1个 B、2个 C、3个 D、4个8. 如图,所提供的信息正确的是( )
A、∠AOD B、∠BOD C、∠BOC D、∠AOD和∠BOC2. 下列方程组中,是二元一次方程组的是( )A、 B、 C、 D、3. 下列选项中的整数,与 最接近的是( )A、3 B、4 C、5 D、64. 若点 在第二象限内,则点 ( )在( )A、 轴正半轴上 B、 轴负半轴上 C、 轴正半轴上 D、 轴负半轴上5. 若 , 则下列不等式中错误的是( )A、 B、 C、 D、6. 国务院在2020年11月1日零时开展了第七次全国人口普查,人口调查采用普查方式的理由是( )A、人口调查的数目不太大 B、受条件限制,无法进行抽样调查 C、人口调查具有破坏性 D、人口调查需要获得全面准确的信息7. 不等式 的非负整数解有( )A、1个 B、2个 C、3个 D、4个8. 如图,所提供的信息正确的是( )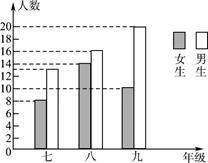 A、七年级学生最多 B、九年级的男生是女生的两倍 C、九年级学生女生比男生多 D、八年级比九年级的学生多9. 下列说法错误的是( )A、过马路的斑马线是平行线 B、100米跑道的跑道线是平行线 C、若a∥b,b∥d,则a⊥d D、过直线外一点有且只有一条直线与已知直线平行10. 若方程组的解 x 和 y 的值相等,则k的值等于( )A、4 B、10 C、11 D、1211. 、、是直线上的三点,是直线外一点,且 , , . 由此可知,点到直线的距离是( )A、 B、不小于 C、不大于 D、在与之间12. 解不等式组 时,不等式①②的解集在同一条数轴上表示正确的是( )A、
A、七年级学生最多 B、九年级的男生是女生的两倍 C、九年级学生女生比男生多 D、八年级比九年级的学生多9. 下列说法错误的是( )A、过马路的斑马线是平行线 B、100米跑道的跑道线是平行线 C、若a∥b,b∥d,则a⊥d D、过直线外一点有且只有一条直线与已知直线平行10. 若方程组的解 x 和 y 的值相等,则k的值等于( )A、4 B、10 C、11 D、1211. 、、是直线上的三点,是直线外一点,且 , , . 由此可知,点到直线的距离是( )A、 B、不小于 C、不大于 D、在与之间12. 解不等式组 时,不等式①②的解集在同一条数轴上表示正确的是( )A、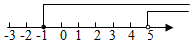 B、
B、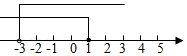 C、
C、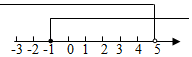 D、
D、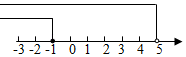
二、填空题
-
13. 实数的相反数是.14. 为了了解线上教学时学校七年级800名学生参加家务劳动的时间,随机对该年级50名学生进行了调查.在这次调查中,样本容量是 .15. 在扇形统计图中,其中一个扇形的圆心角是216°,则这部分扇形所表示的部分占总体的百分数是 .
16. 在3x+4y=9中,如果2y=6,那么x=17. 已知 ,则 .18. 某班级从文化用品市场购买签字笔和圆珠笔共15支,所付金额大于26元,但小于27元,已知签字笔每支2元,圆珠笔每支1.5元,则其中签字笔购买了支.19. a、b、c是直线,且a∥b,b⊥c,则a与c的位置关系是 .20. 如图,点A(1,0),点A第一次跳动到点A1(﹣1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(﹣2,2),第四次向右跳动5个单位至点A4(3,2),…依此规律跳动下去,点A第2022次跳动至点A2022的坐标是 .
三、解答题
-
21. 计算(1)、计算:;(2)、解不等式:(3)、解方程组:(4)、解不等式组:(5)、根据题意将证明过程补充完整:
已知:如图, , 求证: .
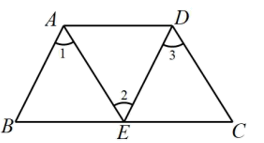
证明:∵(已知)
∴( )
又∵(已知))
∴( )
∴ ▲ ( )
22. 如图,一只蚂蚁从点 沿数轴向右爬了2个单位长度到达点 ,点 表示 ,设点 所表示的数为 .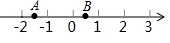 (1)、求 的值;(2)、在数轴上还有 、 两点分别表示实数 和 ,且有 与 互为相反数,求 的平方根.23. 三角形在平面直角坐标系中的位置如图所示.
(1)、求 的值;(2)、在数轴上还有 、 两点分别表示实数 和 ,且有 与 互为相反数,求 的平方根.23. 三角形在平面直角坐标系中的位置如图所示.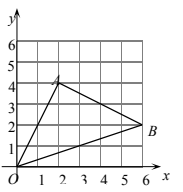 (1)、写出A、B两点的坐标;(2)、经过平移后,三角形中任意一点的对应点为 , 写出A、B两点的对应点的坐标.(3)、求出三角形的面积.24. 小明在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
(1)、写出A、B两点的坐标;(2)、经过平移后,三角形中任意一点的对应点为 , 写出A、B两点的对应点的坐标.(3)、求出三角形的面积.24. 小明在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.分组
频数
百分比
2
5%
6
15%
a
45%
9
22.5%
b
c
2
d
合计
40
100%
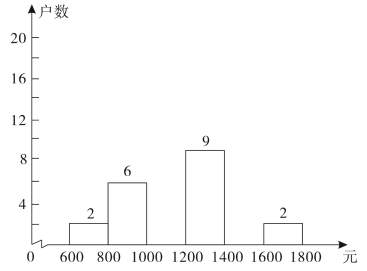
根据以上提供的信息,解答下列问题:
(1)、频数分布表中: , , , .(2)、补全频数分布直方图.(3)、估计该居民小区家庭属于中等收入(不低于1000不足1600元)的大约有多少户?25. 某中学组织一批学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满. 试问:这批学生人数是多少?原计划租用45座客车多少辆?26. 在一次数学综合实践活动课上,同学们进行了如下探究活动:将一块等腰直角三角板的顶点G放置在直线上,旋转三角板.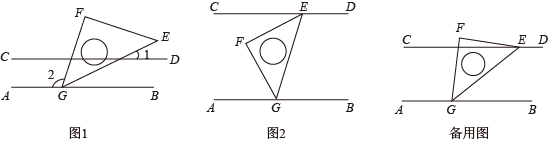 (1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.
(1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.