广东省梅州市平远县2021-2022学年七年级下学期期末考试数学试题
试卷更新日期:2022-09-07 类型:期末考试
一、单选题
-
1. 如图是某一立方体的侧面展开图,则该立方体是( )
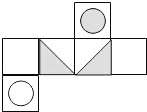 A、
A、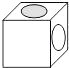 B、
B、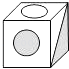 C、
C、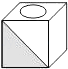 D、
D、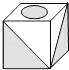 2. 下列运算一定正确的是( )A、 B、 C、 D、3. 从平面镜里看到背后墙上电子钟示数如图所示,这时的实际时间应是( )
2. 下列运算一定正确的是( )A、 B、 C、 D、3. 从平面镜里看到背后墙上电子钟示数如图所示,这时的实际时间应是( ) A、21:05 B、21:15 C、20:15 D、20:054. 如图,在 中,D,E分别是边 , 上的点,若 ,则 的度数为( )
A、21:05 B、21:15 C、20:15 D、20:054. 如图,在 中,D,E分别是边 , 上的点,若 ,则 的度数为( ) A、 B、 C、 D、5. 如图,一只蚂蚁以均匀的速度沿台阶A1→A2→A3→A4→A5爬行,那么蚂蚁爬行高度h随时间t变化的图象大致是( )
A、 B、 C、 D、5. 如图,一只蚂蚁以均匀的速度沿台阶A1→A2→A3→A4→A5爬行,那么蚂蚁爬行高度h随时间t变化的图象大致是( )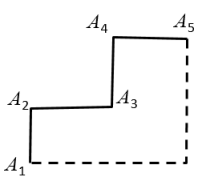 A、
A、 B、
B、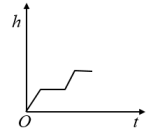 C、
C、 D、
D、 6. 若数轴上A、B两点所对应的有理数分别为a、b,且B在A的右边,则a-b一定( )
6. 若数轴上A、B两点所对应的有理数分别为a、b,且B在A的右边,则a-b一定( )
A、大于零 B、小于零 C、等于零 D、无法确定二、填空题
-
7. 我市某天最高温度是11℃,最低气温是零下3℃,那么当天的最大温差是℃.8. 写出一个只含有字母、的单项式,使它的系数为2,次数为3.9. 的倒数是;的相反数是;-4的绝对值是 .10. 等腰三角形的两边长分别是3cm和6cm,则它的周长是cm.11. 已知:如图,在中, , 过点且平行于 , 若 , 则的度数为 .
 12. 上海世博会“中国馆”的展馆面积为15800 m2 , 这个数据用科学记数法可表示为 m2 .13. 一只蚂蚁自由自在地在用七巧板拼成的正方形中爬来爬去(每块七巧板的表面完全相同),它最终停留在1号七巧板上的概率 .
12. 上海世博会“中国馆”的展馆面积为15800 m2 , 这个数据用科学记数法可表示为 m2 .13. 一只蚂蚁自由自在地在用七巧板拼成的正方形中爬来爬去(每块七巧板的表面完全相同),它最终停留在1号七巧板上的概率 . 14. 我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101)2,(1011)2换算成十进制数应为:(20=1)
14. 我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,如将(101)2,(1011)2换算成十进制数应为:(20=1), ,
按此方式,将二进制(1001)2换算成十进制数的结果是
三、解答题
-
15. 计算:16. 先化简,再求值: , 其中 , .17. 2008年6月1日北京奥运圣火在宜昌传递,圣火传递路线分为两段,其中在市区的传递路程为700(a-1)米,三峡坝区的传递路程为(881a+2309)米.设圣火在宜昌的传递总路程为s米.(1)、用含a的代数式表示s;(2)、已知a=11,求s的值.18. 下面是我县某养鸡场2001~2006年的养鸡统计图:
 (1)、从图中你能得到什么信息?(2)、各年养鸡多少万只?(3)、所得(2)的数据都是准确数吗?(4)、这张图与条形统计图比较,有什么优点?19. 父亲告诉张云:“距离地面越高,温度越低”,并给张云出示了下面的表格:
(1)、从图中你能得到什么信息?(2)、各年养鸡多少万只?(3)、所得(2)的数据都是准确数吗?(4)、这张图与条形统计图比较,有什么优点?19. 父亲告诉张云:“距离地面越高,温度越低”,并给张云出示了下面的表格:距离地面高度(千米)
0
1
2
3
4
5
温度(℃)
20
14
8
2
-4
-10
根据上表,父亲还给张云出了下面几个问题,请你和张云一起回答.
(1)、上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、如果用h表示距离地面的高度,用t表示温度,那么随着的变化,是怎么变化的?(3)、你能猜出距离地面6千米的高空温度是多少吗?20. 小明家里的阳台地面,水平铺设了仅黑白颜色不同的18块方砖(如图),他从房间里向阳台抛小皮球,小皮球最终随机停留在某块方砖上. (1)、求小皮球分别停留在黑色方砖与白色方砖上的概率;(2)、上述哪个概率较大?要使这两个概率相等,应改变第几行第几列的哪块方砖颜色?怎样改变?21. 如图,平面内有公共端点的六条射线 , , , , , , 从射线开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
(1)、求小皮球分别停留在黑色方砖与白色方砖上的概率;(2)、上述哪个概率较大?要使这两个概率相等,应改变第几行第几列的哪块方砖颜色?怎样改变?21. 如图,平面内有公共端点的六条射线 , , , , , , 从射线开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,…. (1)、“25”在射线上;(2)、请用含(为自然数)的代数式表示射线OA、OC、OE上数字的排列规律;(3)、“2009”在哪条射线上?22. 如图,在△ABC中,AD是BC边上的中线,F,E分别是AD及其延长线上的点.
(1)、“25”在射线上;(2)、请用含(为自然数)的代数式表示射线OA、OC、OE上数字的排列规律;(3)、“2009”在哪条射线上?22. 如图,在△ABC中,AD是BC边上的中线,F,E分别是AD及其延长线上的点. (1)、如果CFBE,说明:△BDE≌△CDF;(2)、若CF,BE是△ABC的BC边上的中线AD及其延长线的垂线,垂足分别为E、F,请猜想BF与CE的位置关系?并说明理由.23. 平面内的两条直线有相交和平行两种位置关系,如图,点P在AB、CD外部时,由 , 有∠B=∠BOD,因∠BOD+∠POD=180°,∠POD +∠BPD+∠D =180°,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D.
(1)、如果CFBE,说明:△BDE≌△CDF;(2)、若CF,BE是△ABC的BC边上的中线AD及其延长线的垂线,垂足分别为E、F,请猜想BF与CE的位置关系?并说明理由.23. 平面内的两条直线有相交和平行两种位置关系,如图,点P在AB、CD外部时,由 , 有∠B=∠BOD,因∠BOD+∠POD=180°,∠POD +∠BPD+∠D =180°,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D. (1)、如图,将点P移到AB、CD内部,延长BP交CD于点E,以上结论是否成立?若不成立,则∠BPD、∠B、∠D之间有何数量关系?请说明你的理由;
(1)、如图,将点P移到AB、CD内部,延长BP交CD于点E,以上结论是否成立?若不成立,则∠BPD、∠B、∠D之间有何数量关系?请说明你的理由; (2)、如图,直线AB与直线CD交于点Q,延长BP交CD于点F,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需说明理由);
(2)、如图,直线AB与直线CD交于点Q,延长BP交CD于点F,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需说明理由); (3)、若∠A=60°,∠B=15°,∠E=20°,根据(2)的结论求图中∠AGB的度数.
(3)、若∠A=60°,∠B=15°,∠E=20°,根据(2)的结论求图中∠AGB的度数. 24. 如图,点E在线段CD上,EA、EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,且AD∥BC.
24. 如图,点E在线段CD上,EA、EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,且AD∥BC. (1)、你认为AE和BE有什么位置关系?并验证你的结论;(2)、当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?(3)、在(2)的情况下,此时BF=BC吗?证明你的结论并求出AB的长.
(1)、你认为AE和BE有什么位置关系?并验证你的结论;(2)、当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?(3)、在(2)的情况下,此时BF=BC吗?证明你的结论并求出AB的长.