贵州省六盘水市2021-2022学年九年级上学期第一次月考数学试题

试卷更新日期：2022-09-06 类型：月考试卷

进入出卷网下载

一、单选题

1. 如图，菱形ABCD的周长是4cm，∠ABC＝60°，那么这个菱形的对角线AC的长是（）

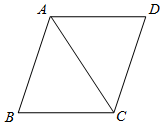A、1cm B、2 cm C、3cm D、4cm

查看试题解析
2. 直角三角形中，两直角边长分别是12和5，则斜边上的中线长是（）

A、2.5 B、6 C、6.5 D、13

查看试题解析
3. 如图，将矩形纸片 $A B C D$ 沿 $B E$ 折叠，使点A落在对角线 $B D$ 上的 $A^{'}$ 处.若 $∠ D B C = 24^{°}$ ，则 $∠ A^{'} E B$ 等于（）.

A、 $66^{°}$ B、 $60^{°}$ C、 $57^{°}$ D、 $48^{°}$

查看试题解析
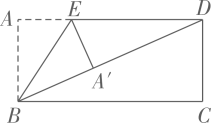4. 如图，四边形 $O B C D$ 是正方形，O ， D两点的坐标分别是 $(0 ， 0)$ ， $(0 ， 6)$ ，点C在第一象限，则点C的坐标是（）

A、 $(6 ， 3)$ B、 $(3 ， 6)$ C、 $(0 ， 6)$ D、 $(6 ， 6)$

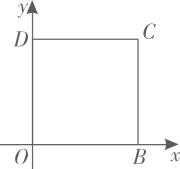查看试题解析
5. 一元二次方程4x²﹣1=5x的二次项系数、一次项系数、常数项分别为（）

A、4，﹣1，5 B、4，﹣5，﹣1 C、4，5，﹣1 D、4，﹣1，﹣5

查看试题解析
6. 代数式x²﹣4x+5的值（）

A、恒为正 B、恒为负 C、可能为0 D、不能确定

查看试题解析
7. 关于x的一元二次方程 $(m - 2) x^{2} + 5 x + m^{2} - 2 m = 0$ 的常数项为0，则m的值为（）

A、1 B、2 C、1或2 D、0

查看试题解析

8. 输入一组数据，按下列程序进行计算，输出结果如表：

x	20.5	20.6	20.7	20.8	20.9
输出	－13.75	－8.04	－2.31	3.44	9.21

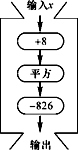
分析表格中的数据，估计方程(x＋8)²－826＝0的一个正数解x的大致范围为（）

A、20.5＜x＜20.6 B、20.6＜x＜20.7 C、20.7＜x＜20.8 D、20.8＜x＜20.9

查看试题解析

9. 如图，正方形ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点，若AC＋BD=8 $\sqrt{2}$ cm，则EF的长度为（）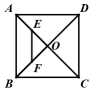

A、1cm B、2cm C、2 $\sqrt{2}$ cm D、4cm

查看试题解析
10. 定义：如果一元二次方程ax²+bx+c＝0（a≠0）满足a﹣b+c＝0，那么我们称这个方程为“蝴蝶”方程．已知关于x的方程ax²+bx+c＝0（a≠0）是“蝴蝶”方程，且有两个相等的实数根，则下列结论中正确的是（　　）

A、b＝c B、a＝b C、a＝c D、a＝b＝c

查看试题解析
11. 九年级举行篮球赛，初赛采用单循环制（每两个班之间都进行一场比赛），据统计，比赛共进行了28场，求九年级共有多少个班．若设九年级共有x个班，根据题意列出的方程是（）

A、x（x﹣1）=28 B、 $\frac{1}{2}$ x（x﹣1）=28 C、2x（x﹣1）=28 D、 $\frac{1}{2}$ x（x+1）=28

查看试题解析
12. 《代数学》中记载，形如 $x^{2} + 8 x = 33$ 的方程，求正数解的几何方法是：“如图1，先构造一个面积为 $x^{2}$ 的正方形，再以正方形的边长为一边向外构造四个面积为 $2 x$ 的矩形，得到大正方形的面积为 $33 + 16 = 49$ ，则该方程的正数解为 $7 - 4 = 3$ ．”小聪按此方法解关于 $x$ 的方程 $x^{2} + 10 x + m = 0$ 时，构造出如图2所示的图形，已知阴影部分的面积为50，则该方程的正数解为（）．

A、6 B、 $5 \sqrt{3} - \frac{3}{2}$ C、 $5 \sqrt{3} - 2$ D、 $5 \sqrt{3} - 5$

查看试题解析

二、填空题

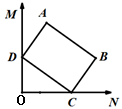
13. 已知方程（x²+y²﹣1）²＝16，则x²+y²的值为．

查看试题解析
14. 方程 $(n - 3) x^{| n | - 1} + 3 x + 3 n = 0$ 是关于x的一元二次方程，则 $n =$ ．

查看试题解析
15. 在四边形ABCD中，AB＝BC＝CD＝DA＝5cm，对角线AC，BD相交于点O，且AC＝8cm，则四边形ABCD的面积为cm² ．

查看试题解析
16. 如图，∠MON=90°，矩形ABCD的顶点C、D分别在边ON，OM上滑动，AB=9，BC=6，在滑动过程中，点A到点O的最大距离为.

查看试题解析

三、解答题

17. 解一元二次方程：

(1)、（x﹣3）（x+3）＝27（用直接开方法）；

(2)、x²+8x+15＝0（用配方法）．

查看试题解析
18. 关于 $x$ 的一元二次方程 $a x^{2} + b x + 1 = 0$ ．

(1)、当 $b = a + 2$ 时，利用根的判别式判断方程根的情况；

(2)、若方程有两个相等的实数根，写出一组满足条件的 $a$ ， $b$ 的值，并求此时方程的根．

查看试题解析
19. 如图，某小区在宽 $20 m$ ，长 $32 m$ 的矩形场地上修同样宽的三条人行道(阴影部分)，余下的部分种花草.若种植花草的面积为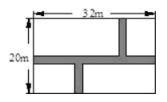 $589 m^{2}$ ，求道路的宽度.

查看试题解析
20. 由多项式乘法：（x+a）（x+b）＝x²+（a+b）x+ab，将该式从右到左使用，即可得到“十字相乘法”进行因式分解的公式：x²+（a+b）x+ab＝（x+a）（x+b）．
示例：分解因式：x²+5x+6＝x²+（2+3）x+2×3＝（x+2）（x+3）．

(1)、尝试：分解因式：x²+6x+8＝（x+）（x+）；

(2)、应用：请用上述方法解方程：
①x²﹣3x﹣4＝0；
②x²﹣7x+12＝0．

查看试题解析
21. 如图：在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线交BC于点E（尺规作图的痕迹保留在图中了），连接EF.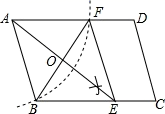

(1)、求证：四边形ABEF为菱形；

(2)、AE，BF相交于点O，若BF＝6，AB＝5，求AE的长.

查看试题解析
22. 如图，在▱ABCD中，对角线AC的垂直平分线EF交AD于点F，交BC于点E，交AC于点O．求证：四边形AECF是菱形．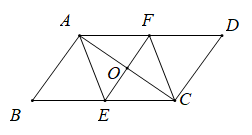
【小海的证明过程】
证明：∵EF是AC的垂直平分线，
∴OA＝OC，OE＝OF，EF⊥AC，
∴四边形AECF是平行四边形．
又∵EF⊥AC，
∴四边形AECF是菱形．
【老师评析】
小海利用对角线互相平分证明了四边形AECF是平行四边形，再利用对角线互相垂直证明它是菱形，可惜有一步错了．
【挑错改错】

(1)、请你帮小海找出错误的原因；

(2)、请你根据小海的思路写出此题正确的证明过程．

查看试题解析
23. 如图，正方形ABCD中，点E在BC的延长线上，AE分别交DC，BD于F，G，点H为EF的中点．求证：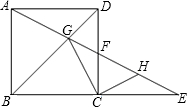

(1)、∠DAG＝∠DCG；

(2)、GC⊥CH．

查看试题解析
24. 如图，在平行四边形ABCD中，点M，N是AD边上的点，BM，CN交于点O，AN＝DM，BM＝CN．

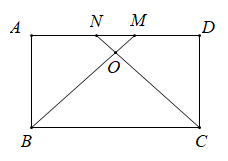(1)、求证：平行四边形ABCD是矩形．

(2)、若∠BOC＝90°，MN＝1．AM•MD＝12，求四边形ABCD的面积．

查看试题解析
25. 已知：正方形ABCD中，∠MAN＝45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M，N．

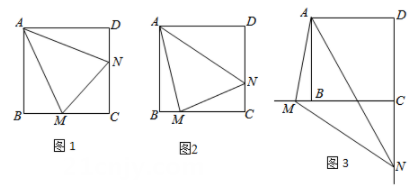(1)、当∠MAN绕点A旋转到BM=DN时（如图1）的位置时，求证：BM+DN＝MN；

(2)、当∠MAN绕点A旋转到BM≠DN时（如图2），则线段BM，DN和MN之间数量关系是；

(3)、当∠MAN绕点A旋转到如图3的位置时，猜想线段BM，DN和MN之间又有怎样的数量关系呢？并对你的猜想加以说明．

查看试题解析