湖北省省直辖县级行政单位潜江市2021-2022学年九年级上学期10月月考数学试题
试卷更新日期:2022-09-06 类型:月考试卷
一、单选题
-
1. 下列方程中是关于x的一元二次方程的是( )A、 B、 C、 D、2. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、3. 对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )A、开口向下 B、对称轴是x=﹣1 C、顶点坐标是(1,2) D、最大值是24. “杂交水稻之父”袁隆平和他的团队探索培育的“海水稻”在某试验田的产量逐年增加,2018年平均亩产量约500公斤,2020年平均亩产量约800公斤.若设平均亩产量的年平均增长率为x , 根据题意,可列方程为( )A、 B、 C、 D、5. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、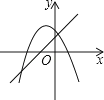 B、
B、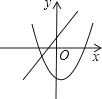 C、
C、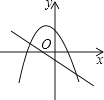 D、
D、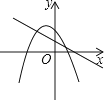 6. 已知m,n是一元二次方程 的两个实数根,则代数式 的值等于( )A、2019 B、2020 C、2021 D、20227. 关于 的方程 有实数根,则k的取值范围是( )A、 且 B、 且 C、 D、8. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:
6. 已知m,n是一元二次方程 的两个实数根,则代数式 的值等于( )A、2019 B、2020 C、2021 D、20227. 关于 的方程 有实数根,则k的取值范围是( )A、 且 B、 且 C、 D、8. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:…
-2
0
1
3
…
…
6
-4
-6
-4
…
下列各选项中,正确的是
A、这个函数的图象开口向下 B、这个函数的图象与x轴无交点 C、这个函数的最小值小于-6 D、当 时,y的值随x值的增大而增大9. 已知关于x的一元二次方程有两个不相等的实数根 , , 且 , 满足 , 则a的值为( )A、 B、 C、1或 D、6或10. 如图,在菱形ABCD中, , ,点P , Q同时从点A出发,点P以1cm/s的速度沿A﹣C﹣D的方向运动,点Q以2cm/s的速度沿A﹣B﹣C﹣D的方向运动,当其中一点到达D点时,两点停止运动.设运动时间为x(s), 的面积为y(cm2),则下列图象中能大致反映y与x之间函数关系的是( )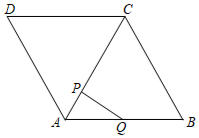 A、
A、 B、
B、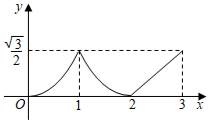 C、
C、 D、
D、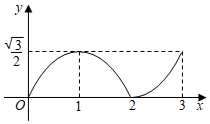
二、填空题
-
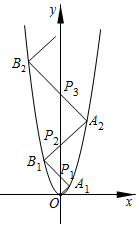
11. 一元二次方程x(x﹣7)=8(7﹣x)的根是 .12. 关于x的一元二次方程mx2﹣2x+1=0有两个不相等的实数根,则实数m的取值范围是 .13. 把抛物线y=2x2+1向右平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为 .14. 若等腰三角形的一边长是4,另两边的长是关于 的方程 的两个根,则 的值为 .15. 已知方程(a2+b2)2+a2+b2=6,则a2+b2的值是 .16. 如图,抛物线解析式为y=x2 , 点A1的坐标为(1,1),连接OA1;过A1作A1B1⊥OA1 , 分别交y轴、抛物线于点P1、B1;过B1作B1A2⊥A1B1分别交y轴、抛物线于点P2、A2;过A2作A2B2⊥B1A2 , 分别交y轴、抛物线于点P3、B2…;则点Pn的坐标是 .
三、解答题
-
17. 解方程:(1)、2x2﹣3x+1=0;(2)、(2x﹣3)2=(3x+1)2 .18. 在西安市争创全国教育强市的宏伟目标指引下,高新一中初中新校区在今年如期建成.在校园建设过程中,规划将一块长18米,宽10米的矩形场地建设成绿化广场,如图,内部修建三条宽相等的小路,其中一条路与广场的长平行,另两条路与广场的宽平行,其余区域种植绿化,使绿化区域的面积为广场总面积的80%,求广场中间小路的宽.
 19. 已知某抛物线的顶点为(2,4),且过点(1,2).(1)、求抛物线的解析式;(2)、动点P(a,6)能否在抛物线上?请说明理由;(3)、若点A(m,y1),B(n,y2)都在抛物线上,且m<n<0,比较y1 , y2的大小,并说明理由.20. 关于 的一元二次方程 有实数根.(1)、求 的取值范围;(2)、如果 是符合条件的最大整数,且一元二次方程 与方程 有一个相同的根,求此时 的值.21. 已知关于x的一元二次方程x2﹣(k+3)x+2k﹣1=0.(1)、求证:无论k取何值,方程都有两个不相等的实数根.(2)、若该方程的两个实数根分别为x1、x2 , 且x12+x22=14,求k的值.22. 某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.(1)、当销售单价为90元时,每月的销售量为件.(2)、求该商品每月的销售量y(件)与销售单价x(元)之间的函数关系式;(不需要求自变量取值范围)(3)、若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?23. 已知二次函数y=﹣x2+6x﹣5.(1)、求二次函数图象的顶点坐标;(2)、当1≤x≤4时,函数的最大值和最小值分别为多少?(3)、当t≤x≤t+3时,函数的最大值为m,最小值为n,求t的值.24. 如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于点A(﹣1,0)、B(3,0),交y轴于点C.
19. 已知某抛物线的顶点为(2,4),且过点(1,2).(1)、求抛物线的解析式;(2)、动点P(a,6)能否在抛物线上?请说明理由;(3)、若点A(m,y1),B(n,y2)都在抛物线上,且m<n<0,比较y1 , y2的大小,并说明理由.20. 关于 的一元二次方程 有实数根.(1)、求 的取值范围;(2)、如果 是符合条件的最大整数,且一元二次方程 与方程 有一个相同的根,求此时 的值.21. 已知关于x的一元二次方程x2﹣(k+3)x+2k﹣1=0.(1)、求证:无论k取何值,方程都有两个不相等的实数根.(2)、若该方程的两个实数根分别为x1、x2 , 且x12+x22=14,求k的值.22. 某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.(1)、当销售单价为90元时,每月的销售量为件.(2)、求该商品每月的销售量y(件)与销售单价x(元)之间的函数关系式;(不需要求自变量取值范围)(3)、若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?23. 已知二次函数y=﹣x2+6x﹣5.(1)、求二次函数图象的顶点坐标;(2)、当1≤x≤4时,函数的最大值和最小值分别为多少?(3)、当t≤x≤t+3时,函数的最大值为m,最小值为n,求t的值.24. 如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于点A(﹣1,0)、B(3,0),交y轴于点C.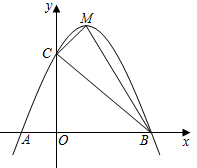 (1)、求此二次函数的解析式;(2)、若点M是该二次函数图象上第一象限内一点,且S△BCM=3,求点M的坐标;(3)、在二次函数图象上是否存在一点P使△BCP是以BC为底边的等腰三角形,若不存在,请说明理由,若存在,请求出点P的坐标.
(1)、求此二次函数的解析式;(2)、若点M是该二次函数图象上第一象限内一点,且S△BCM=3,求点M的坐标;(3)、在二次函数图象上是否存在一点P使△BCP是以BC为底边的等腰三角形,若不存在,请说明理由,若存在,请求出点P的坐标.